Curriculum di piero pistoia
cliccare su:
piero-pistoia-curriculumok (#)
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
PER LEGGERE IL POST IN PDF CLICCARE SUL LINK SOTTO; PER TORNARE A LEGGERE LO SCRITTO DOPO IL LINK, TORNARE INDIETRO PREMENDO SULLA FRECCIA IN ALTO A SINISTRA
VERSO IL PERIODOGRAMMA0
ATTENZIONE QUESTO LAVORO VIENE CONTINUAMENTE DANNEGGIATO SPECIALMENTE NEGLI SCRIPTS NONOSTANTE LE CORREZIONI! (Piero Pistoia)
UN PERCORSO VERSO IL ‘PERIODOGRAMMA’ ATTRAVERSO ALCUNI CONCETTI PORTANTI DELL’ANALISI DELLE SERIE STORICHE
ATTENZIONE: INTERVENTI IN VIA DI COSTRUZIONE! La via si fa con l’andare!
PREMESSA
L’autore di questo scritto, prof. Piero Pistoia, docente di Fisica, avvalendosi del supporto dialettico del collega di Matematica, prof. Pier Francesco Bianchi, stanno lavorando ad un progetto per cercare di automatizzare il processo di analisi di una serie storica reale, usando il linguaggio R ed il MATHEMATICA di Wolfram, cercando di usare comandi di basso livello. Ci apriamo il sentiero nell’andare per cui non sarà rettilineo ma complesso e intrecciato e spesso dovremo tornare indietro, persi nei meandri di questo ‘zibaldone’ alla Leopardi di statistiche e programmazioni. Una cosa è certa però: ci stiamo divertendo e andremo avanti e forse chissà se ci fermeremo.
L’obbiettivo di questo lavoro è fornire strumenti direttamente operativi al lettore perché possa scoprire all’interno di una serie storica componenti rilevanti della sua variazione. Faremo una sintesi argomentativa sui concetti di statistica implicati nello studio di una serie storia (correlogramma, periodogramma, media mobile, regressione lineare, analisi dei residui…) fino a ‘leggere’ all’interno di serie specifiche, seguendo un itinerario guidato.
Abbiamo iniziato “forzando” R a raccogliere informazioni preliminari sulla serie in studio per poi intervenire su essa correggendo ed aggiustando ( correzione degli outliers, interpolazioni per mancanza di dati, ecc.). Sorge poi il problema di cosa cercare all’interno dei dati e come cercarlo a partire da grafici e altri tests (correlogrammi e periodogrammi ecc.). A questo punto si è posto il problema di “fittare” una combinazione di onde del seno ai dati di una serie storica sperimentale usando il metodo dei minimi quadrati. Una volta imparato come calcolare i coefficienti di una regressione lineare, appunto condotta sui dati con una combinazione polinomiale di funzioni sinusoidali, cercheremo di precisare con esempi il processo chiamato Analisi armonica di Fourier.
Ma oggi, in questo contesto, ci siamo soffermati a riflettere su come possiamo, utilizzando sempre il linguaggio R e il MATHEMATICA di Wolfram, costruire il cosiddetto Periodogramma di una serie storica che possa individuare, se ci sono, oscillazioni sinusoidali rilevanti. Il Periodogramma in generale riporta sulle ascisse valori in successione, ognuno dei quali rappresenta il numero delle oscillazioni complete che quella particolare onda compie in n dati (così,se n=60, 5 rappresenta la presenza nei dati di una oscillazione che fa 5 cicli completi in 60 dati, cioè di periodo 12). Le oscillazioni rilevanti, suggerite dal Periodogramma, possono essere tolte poi dai dati originali (destagionalizzazione), per esempio, con medie mobili opportune, onde iniziare la scomposizione della serie stessa e così via.
Vi proponiamo allora, nel prosieguo, attraverso un percorso piuttosto lungo ed articolato, punteggiato di concetti ed esempi di calcolo, come obbiettivo ‘regolativo’ s.l., versioni di Periodogramma, scritte in R e in Mathematica di Wolfram (Piero Pistoia), che pur non ottimizzate, riescano efficacemente a funzionare su due esempi, uno da noi controllato ed l’altro reale.
Tutto quello che verrà detto durante questo lavoro, pur non avendo la pretesa di esaurire le problematiche ivi implicate (per questo vedere bibliografia), speriamo aiuterà il lettore, se interessato, a seguire l’analisi di una serie storica, attraverso cammini meno usuali e teorici, fornendo strumenti operativi per poter affrontare studi più organizzati in un secondo momento.
I conti possono essere seguiti su una qualsiasi spread-sheet oppure attraverso tre programmi in Qbasic allegati (scritti dallo stesso Piero Pistoia), poco curati nella forma, ma che contengono routines efficaci, e/o utilizzando, come abbiamo accennato, i comandi di due grossi programmi di statistica, il programma R ed il linguaggio del Mathematica di Wolfram.
IL CORRELOGRAMMA: UNA ‘LENTE’ PER STUDIARE IN UNA SERIE STORICA VARIE COMPONENTI DELLA SUA VARIAZIONE
All’interno di una serie storica reale, per es., dei 60 ( mg/l) dati mensili yt della concentrazione As nelle acque della Carlina, che a più riprese analizzeremo, è possibile individuare varie serie componenti: a) una o più serie stagionali, nel senso lato della parola, cioè oscillazioni regolari, periodiche, in accordo col calendario o con l’orologio; b) una serie corrispondente al trend o variazione a lungo termine della media, che di fatto comprende tutte le componenti cicliche la cui lunghezza d’onda supera la serie temporale osservata, cioè supera lo stesso range dei dati; c) uno o più cicli, cioè fluttuazioni irregolari intorno ad una tendenza a lungo termine, non periodiche (almeno all’interno dei dati) talora intermittenti, di durata variabile, non correlate al calendario, i cui effetti durano oltre i dati, ma coglibili anche all’interno del range dei dati, d) la componente irregolare o casuale (random) che riassume lo “white noise” e infine e) qualche componente occasionale o erratica (periodo di siccità, terremoto, sciopero…).
Sintetizzando, possiamo ragionevolmente affermare che i dati annuali tipicamente esibiscono un trend ed un effetto ciclico, ma non un effetto stagionale. Ci sono però anche eccezioni: si pensi agli effetti stagionali di periodo superiore a qualche anno di alcuni fenomeni astronomici (ciclo delle macchie solari, di periodo circa 11 anni, che forse può attivare altri fenomeni analoghi nell’atmosfera). I dati mensili e quelli ‘quaterly’ (relativi ad 1/4 di anno, cioè trimestrali), probabilmente mostrano trend e influenze stagionali, ma usualmente non componenti cicliche a meno che i dati coinvolgano molti anni. In generale gli effetti stagionali sono visti come oscillazioni ripetitive entro il tempo di un anno. Sono comprese negli effetti stagionali anche le oscillazioni all’interno delle 24 ore per dati orari e le oscillazioni all’interno della settimana e all’interno del mese per dati giornalieri.
Prima di cercare di scomporre nelle sue componenti elementari una serie storica, conviene dare uno sguardo al suo contenut con un grafico opportuno, con lo strumento Correlogramma ( [1] pagg. 376-390) e con il Periodogramma, che presenteremo definitivo al termine del lavoro, strumenti essenziali anche per l’analisi dei RESIDUI.
Il coefficiente di correlazione di Pearson misura la correlazione fra due variabili aleatorie che dipendono linearmente l’una dall’altra. Ha valore +1 se le due variabili variano linearmente in fase e -1 se variano in controvase. Questo coefficiente acquista valori fra -1 e +1. Il coefficiente di correlazione di Pearson dipende dalla covarianza, covarianza=Somma[(x-xm)*(y-ym]/n, e dalla deviazione standard di entrambe le variabili: coeff. di correlazione=Covarianza/(DSx*DSy).
I coefficienti di auto-correlazione rh, dove h=0,1,2…q con q minore od uguale a (n-2)/2, sono coefficienti di correlazione, calcolati per ogni valore di h, che misurano la concordanza o la discordanza fra i valori di una serie storica e quelli della stessa però slittati di h unità di tempo (lag h), consentendo di analizzare la sua struttura interna, ossia i legami fra i termini della stessa ([8] 18-20).
rh = Σi[(y(t)-ym)(y(t+h)-ym)]/[(n-h)*Σj(y(t)-ym)^2/n)] dove i va da t=1…n-h e j va da t=1 … n-h # da togliere l’ultima h!!!
in alcuni testi viene abolito il fattore n/(n-h).
Tale formula presenta la semplificazione di poter utilizzare una media unica per le yt (quella dei dati originali), presupponendo una situazione stazionaria ([8] pag. 19 e [2] pag. 133). In particolare ro=1 (lag h=0), nessun slittamento e gli altri rh assumono valori fra +1 (completa concordanza) e -1 (totale discordanza).
Il correlogramma è la rappresentazione grafica dei coefficienti di auto-correlazione, che sono (n-2)/2, in funzione degli slittamenti (lag h) e ci permette di vedere se la serie storica possiede qualche regolarità interna.
I coefficienti di auto-correlazione di dati random hanno distribuzione campionaria che può essere approssimata da una curva gaussiana con media zero e errore standard 1/√(n). Questo significa che il 95% di tutti i coeff. di auto-cor., calcolati da tutti i possibili campioni estratti, dovrebbero giacere entro un range specificato da: zero ± 1.96*1/√(n) (1.96 errori standard). I dati cioè della serie saranno da considerare random, se i coeff. di auto-cor. staranno entro i limiti:
-1.96*(1/√n) ≤ rh ≤ +1.96*(1/√n) fascia dell’errore: +/- 2/√n
Per l’interpretazione dei correlogrammi vedere [8] 20-25.
– In una serie storica completamente casuale, i cui successivi valori sono considerati tutti indipendenti fra loro (non correlati), tutti i valori rh, eccetto ro che è sempre +1 ( correlazione della serie con se stessa), oscilleranno in maniera casuale intorno allo zero entro la fascia dell’errore.
– I coefficienti di correlazione per dati stazionari (assenza di trend) vanno velocemente a zero dopo 3-4 lags di tempo (forse fino a 5), mentre nella serie non stazionaria, essi sono significativamente diversi da zero per varie unita di tempo anche se tendono a diminuire, es., serie che contiene trend (vedere graf. yt). Nella serie stazionaria esiste una persistenza di valori positivi o negativi a breve termine (se per es., il valore è più alto della media in un mese, lo sarà anche in uno o due mesi successivi. Data la brevità di questo fenomeno (fino a 5 lags max) si riscontra anche in correlogrammi di componenti erratiche.
-Anche col periodogramma (talora detto spettrogramma) è possibile individuare componenti oscillanti, ma anche i trends così da poterli eliminare dalla serie. Come primo input: qualsiasi serie temporale composta di n osservazioni ugualmente spaziate può essere decomposta tramite il metodo dei minimi quadrati in un numero di onde del seno di data frequenza, ampiezza e fase, soggette alle seguenti restrizioni: se n è dispari, allora il numero max di onde fittate è (n-1)/2, se n è pari tale numero è N/2-1. Da notare che in una serie temporale discreta, poichè non appaiono di fatto angoli da trattare, nella definizione di lunghezza d’onda e fase si fa riferimento alle unità di tempo usate per definire la serie, o al numero delle osservazioni n che ‘costruiscono’ la lunghezza d’onda.
– Se la serie storica presenta oscillazioni (stagionali: oscillazioni orarie, giornaliere, settimanali, mensili …), anche il correlogramma tende ad assumere valori positivi e negativi, oscillando con lo stesso periodo della serie in studio fino a smorzarsi ai lags più elevati. Inoltre, se esiste, per es., una componente stagionale di periodo 12 mesi, il valore corrispondente al lag 12 sarà significativamente diverso da zero.
Talora però la lettura del correlogramma risulta ardua. Un modo veloce e quantitativo per testare l’ipotesi che esista all’interno di una serie storica correlazione fra i suoi termini, cioè i termini non siano indipendenti, è somministrare alla serie il test di Durbin e Watson ([3] 949-951), la cui statistica è espressa dalla formula:
d = Σ[e(i)-e(i-1)^2]/Σei^2
La sommatoria al numeratore inizia al 2° termine (i=2= e coinvolge n-1 termini. la statistica d varia da 0 a 4 e quando l’ipotesi nulla è vera (autocorrelazione assente) d dovrebbe essere vicino a 2. Il test permette di decidere di respingere l’ipotesi nulla, di accettarla ovvero essere inconclusivo. Utilizzando la tabella opportuna (allegata) si ottengono i valori critici dl e du che servono per la decisione: all’interno dell’intervallo dl-du, la situazione è incerta; a sinistra di dl, si respinge l’ipotesi nulla.
Il programma CORR, scritto da Piero Pistoia nel glorioso Qbasic (saturo di nostalgia e giovinezza) e allegato a questo scritto, permette il calcolo dei coefficienti di autocorrelazione con l’errore e il calcolo della statistica di Durbin-Wtson; un qualsiasi programma di grafica poi permetterà di costruire il correlogramma sottoponendo ad esso i coefficienti di auto-corr. trovati. Il correlogramma verrà naturalmente ottenuto anche direttamente con i linguaggi di livello R ed il Mathematica di Wolfram. CORR infine fa anche l’analisi armonica.
ESERCIZI DI COSTRUZIONE E ‘LETTURA’ DEL CORRELOGRAMMA
Consideriamo la serie storica mensile yt di 60 dati della concentrazione As già nominata. Inseriamo in CORR vari vettori dati da analizzare, mutuati da questo studio (per es., yt, ESAs (Effetto stagionale), Yt1=yt-ESAs (Ciclo+Trend+Random), Yt1_smussato dai random …), nei comandi DATA al capoverso SERIE STORICA ORIGINALE. Successivamente possiamo trasformare in remarks le precedenti linee yt e aprire quelle successive, EFFETTO STAGIONALE As (ESAs), se gira il programma, troveremo il dati del correlogramma per la serie ESAs. Per aprire e chiudere i DATA si usa l’apice ‘. Naturalmente possiamo introdurre la serie che vogliamo (es., RESIDUI..). Il programma nei due casi accennati, lanciato, fornirà 1) La tabella dei coefficienti di auto-correlazione 2)La statistica di Durbin Watson per controllare se c’è autocorrelazione nella serie in studio 3)La statistica di LinMudholcar che è un test sulla gaussiana; 4) L’analisi di Fourier (per ora sospesa). Basta riscrivere le linee di programma nella console del Qbasic.
Scriveremo poi un programmino in R per ottenere gli stessi risultati, molto più agile per avere comandi di livello superiore .Chi vuole può ottenere gli stessi risultati anche con lo straordinario Mathematica di Wolfram o addirittura con EXCEL.
SCRIPT IN Qbasic
‘ PROGRAMMA N. 1
CLS
PRINT TAB(15); “TESTS DI AUTOCORRELAZIONE E NORMALITA'”
PRINT
PRINT TAB(14); “Programma scritto a cura del DOTT. PIERO PISTOIA”
LOCATE 10, 5
PRINT “Il programma calcola: “: PRINT
PRINT TAB(5); “1-I coefficienti di AUTOCORRELAZIONE”
PRINT TAB(5); “2-Il test di DURBIN-WATSON, che misura la correlazione interna”
PRINT TAB(5); “3-Il nuovo test di LIN-MUSHOLKAR per la normalit…”
PRINT TAB(5); “4-L’ANALISI SPETTRALE LINEARE per il periodogramma”
PRINT : PRINT TAB(5); ” Nei punti 2 e 3 consultare le tabelle; dei’cutoff values'”
2 IF INKEY$ = “” THEN 2
CLS
DIM x(100), m(100), sd(100), L(100), rh(100), e(100), g(100), f(100)
INPUT “Immetti il numero dei dati “, n
INPUT “Immetti il numero dei lags h “, n1
‘FOR i = 1 TO n
‘PRINT “x(“; i; : INPUT “)=”, x(i): f(i) = x(i)
‘s(0) = s(0) + x(i)
‘NEXT i
‘GOTO 14
PRINT “CALCOLO DEI COEFFICIENTI DI AUTOCORRELAZIONE”
PRINT
CLS : PRINT “TABELLA DEI COEFFICIENTI DI AUTOCORRELAZIONE”: PRINT
LPRINT “TABELLA DEI COEFFICIENTI DI AUTOCORRELAZIONE”: LPRINT
FOR i = 1 TO n
READ x(i): f(i) = x(i)
s(0) = s(0) + x(i)
NEXT i
xm = s(0) / n
PRINT
PRINT “LAG h”, “COEFF. AUTOCORRELAZIONE”
PRINT
FOR h = 1 TO n1
FOR t = 1 TO n – h
so = (x(t) – xm) * (x(t + h) – xm): s(1) = s(1) + so
NEXT t
FOR t = 1 TO n
so = (x(t) – xm) ^ 2: s(2) = s(2) + so
NEXT t
rh(h) = n * s(1) / ((n – h) * s(2))
PRINT h, rh(h)
s(1) = 0: s(2) = 0
NEXT h
er = 2 / (SQR(n))
PRINT
PRINT “ERROR +/- “, er
s(0) = 0: s(1) = 0: s(2) = 0
PRINT
73 a$ = INKEY$: IF a$ = “” THEN 73
23 LPRINT “LAG H”, “COEFF.AUTOCORRELAZIONE”: LPRINT
FOR i = 1 TO n1: LPRINT USING “###”; i;
LPRINT USING ” #.###”; rh(i): NEXT i
LPRINT : LPRINT “er=”, er
GOTO 20
13 RESTORE
CLS : s(1) = 0: s(2) = 0
PRINT : PRINT “LIN-MUDHOLKAR TEST PER LA GAUSSIANA (TEST DI NORMALITA’)”
21 FOR a = 1 TO n
FOR i = 1 TO n
b = i
IF i = a THEN READ x(i): k = 1: GOTO 7
READ x(b): v = x(b)
IF k = 1 THEN b = i – 1
x(b) = v
7 NEXT i
k = 0
‘FOR i = 1 TO n – 1
‘PRINT x(i); : NEXT i
GOSUB 1000
s(1) = 0: s(2) = 0
RESTORE
NEXT a
‘SERIE STORICA ORIGINALE eliminati 3 autliers
‘ DATA .033,.043,.051,.059,.061,.063,.053,.036,.046,.056,.063,.048,.053,.043
‘ DATA .066,.053,.082,.06,.08,.076,.056,.036,.05,.053,.056,.058,.061,.063,.065
‘ DATA .068,.0815,.095,.079,.063,.069,.074,.08,.0765,.073,.0695,.066,.093,.083
‘ DATA .073,.063,.074,.067,.06,.086,.08,.073,.067,.089,.064,.087,.079,.07,.065
‘ DATA .06,.063
‘EFFETTO STAGIONALE (modello additivo)
‘DATA .0022,-.0030,.0002,-.0053,.0070,.0026,.0107,.0054,-.0042,-.0083,-.0037
‘DATA -.0075,.0022,-.0030,.0002,-.0053,.0070,.0026,.0107,.0054,-.0042,-.0083
‘DATA -.0037,-.0075,.0022,-.0030,.0002,-.0053,.0070,.0026,.0107,.0054,-.0042
‘DATA -.0083,-.0037,-.0075,.0022,-.0030,.0002,-.0053,.0070,.0026,.0107,.0054
‘DATA -.0042,-.0083,-.0037,-.0075,.0022,-.0030,.0002,-.0053,.0070,.0026,.0107
‘DATA .0054,-.0042,-.0083,-.0037,-.0075
DATA 30,29,34,61,54,63,62,41,43,30,35,19,21,25,36
s(1) = 0: s(2) = 0: s(3) = 0: s(4) = 0: s(5) = 0
FOR i = 1 TO n
s(1) = s(1) + m(i): ‘Sum(X)
s(2) = s(2) + m(i) ^ 2: ‘SUM((X)^2)
s(3) = s(3) + m(i) * L(i): ‘SUM(X*Y)
s(4) = s(4) + L(i): ‘SUM(Y)
s(5) = s(5) + L(i) ^ 2: ‘SUM((Y)^2)
NEXT i
PRINT
‘PRINT s(1); s(2); s(3); s(4); s(5)
r = (n * s(3) – s(1) * s(4)) / (SQR(n * s(2) – s(1) ^ 2))
r = r * SQR(n * s(5) – s(4) ^ 2)
PRINT
PRINT “r=”, r
PRINT : PRINT
74 IF INKEY$ = “” THEN 74
LPRINT “STATISTICA DI LIN-MUDHOLKAR PER LA GAUSSIANA”
LPRINT : LPRINT “r=”, r
8 IF INKEY$ = “” THEN 8 ELSE 14
20 PRINT
PRINT “TEST STATISTICO DI DURBIN-WATSON PER L’AUTOCORRELAZIONE”
PRINT : PRINT
s(1) = 0: s(2) = 0
FOR i = 2 TO n
y = x(i) – x(i – 1)
s(1) = s(1) + y ^ 2
NEXT i
FOR i = 1 TO n
y = x(i) ^ 2
s(2) = s(2) + y
NEXT i
DW = s(1) / s(2)
PRINT “DW= “, DW
72 a$ = INKEY$: IF a$ = “” THEN 72
LPRINT : LPRINT “STATISTICA DI DURBIN-WATSON PER L’AUTOCORRELAZIONE”
LPRINT : LPRINT “DW=”, DW
LPRINT
1 a$ = INKEY$: IF a$ = “” THEN 1 ELSE 13
14 PRINT : PRINT ” ANALISI DI FOURIER E PERIODOGRAMMA”: PRINT
t = n
p1 = INT((n – 1) / 2) ‘max frequenza
c1 = COS(2 * 3.1415926# / t)
s1 = SIN(2 * 3.1415926# / t)
s = 0: p = 0
c = 1
210 u1 = 0: u2 = 0
k = t
230 u = f(k) + 2 * c * u1 – u2
u2 = u1
u1 = u
k = k – 1
IF k 0 THEN 340
a = a / 2
PRINT “COEFFICIENTI DI FOURIER”
PRINT TAB(4); “P”; TAB(12); “ALFA”; TAB(21); “BETA”
LPRINT : LPRINT “COEFFICIENTI DI FOURIER”: LPRINT
LPRINT TAB(3); “P”; TAB(12); “ALFA”; TAB(21); “BETA”: LPRINT
340 PRINT USING “##.##^^^^”; p; a; b: LPRINT USING “###”; p;
LPRINT USING ” ##.##^^^^”; a; b
IF p = 0 THEN 480
e(p) = SQR(a * a + b * b)
t2 = ABS(a / b)
t2 = 360 / 2 / 3.1415926# * ATN(t2)
IF b > 0 THEN 450
IF a > 0 THEN 430
t2 = 180 + t2
GOTO 470
430 t2 = 180 – t2
GOTO 470
450 IF a > 0 THEN 470
t2 = 360 – t2
470 g(p) = t2
480 IF p = p1 THEN 540
q = c1 * c – s1 * s
s = c1 * s + s1 * c
c = q
p = p + 1
GOTO 210
540 PRINT : PRINT
PRINT ” ANALISI ARMONICA”: PRINT
LPRINT : LPRINT “ANALISI ARMONICA”: LPRINT
PRINT ” FR”; TAB(6); “FREQ1”; TAB(15); “PERIOD”; TAB(23); “AMPIEZZA”; TAB(34); “FASE”
LPRINT ” FR”; TAB(6); “FREQ1”; TAB(15); “PERIOD”; TAB(23); “AMPIEZZA”; TAB(34); “FASE”
LPRINT
FOR i = 1 TO p1: k1 = n / i: k2 = i / n
PRINT USING “###”; i;
PRINT USING “##.##^^^^”; k2; k1; e(i); g(i)
LPRINT USING “###”; i;
LPRINT USING “##.##^^^^”; k2; k1; e(i); g(i)
NEXT i
75 IF INKEY$ = “” THEN 75
CLS
15 END
1000 FOR i = 1 TO n – 1
s(1) = s(1) + x(i)
NEXT i
m(a) = s(1) / (n – 1)
FOR i = 1 TO n – 1
y1 = x(i) – m(a)
s(2) = y1 ^ 2 + s(2)
NEXT i
sd(a) = SQR(s(2) / (n – 2))
L(a) = sd(a) ^ (2 / 3)
‘PRINT m(A); sd(A); l(A)
RETURN
SCRIPTS IN R PER IL CALCOLO DEI COEFFICIENTI DI CORRELAZIONE DELLA SERIE STORICA REALE yt IN VIA DI ANALISI A del dott. Piero Pistoia
QUESTO PARAGRAFO E’ in via di correzione!
# Intanto trascriviamo nel vettore yt i 60 dati della conc. As da cui partire. Impariamo poi a calcolare con R gli altri 5 vettori dati che faranno parte dell’analisi della nostra serie
reale e quindi della nostra esercitazione. Calcoliamo come primo vettore Mt (media mobile di ordine 12 su yt.
yt=c(.033,.043,.051,.059,.061,.063,.053,.036,.046,.056,.063,.048,.053,.043,.066,.053,.082,.06,.08,.076,.056,.036,.05,.053,
.056,.058,.061,.063,.065,.068,.0815,.095,.079,.063,.069,.074,.08,
.0765,.073,.0695,.066,.093,.083,.073,.063,.074,.067,.06,.086,.08,.073,.067,.089,.064,.087,.079,.07,.065,.06,.063)
t=1
#Come primo passo grafichiamo i dati e osserviamo se ci sono regolarità all’interno (trend, oscillazioni), precisiamo le ipotesi con un correlogramma ed un periodogramma, I dati sono mensili: Ipotizziamo comunque una oscillazione di periodo 12.
# Calcoliamo, come primo vettore, Mt (media mobile centrata e pesata di ordine 12 su yt).
yt=as.vector(yt) ; n=length(yt); Mt=c()
for(t in 7:n){Mt[t] = ((yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+
yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+(yt[t+6])/2)/13}
Mt # non gira! dice che esiste una } in più. Ris=0! In effetti, non so perchè, è apparsa una tonda in più, che continua ad apparire anche se corretta!
for(t in 7:n){Mt[t] = (yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+
yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+(yt[t+6])/2)/13}
mt=filter(yt,filter=rep(1/13,13))
# calcolo della Mm col comando filter di R: confrontare i due risultati
mt #OK
# in Mt ci sono i 48 (60-12) dati Media mobile di yt, da cui costruisco i 12 Fattori Stagionali (FStag) facendo la media dei 4 gennaio, dei 4 febbraio ecc. a partire da luglio, perchè Mt iniziava con luglio.
FSTag0=matrix(Mt, ncol=12, byrow=T)
# matrice di 4 righe (valori dei 12 mesi dei 4 anni) e 12 colonne con in ognuna le 4 conc. dei mesi dello stesso nome a partire da un luglio.
FStag1=colMeans(FSTag0)
# in FStag1 trovo le 12 medie dei 4 mesi dello stesso nome (inizio luglio, fine giugno)
FStag=c( ,FStag1[7:12], FStag1[1:6]) # da controllare! Ordino da gennaio. NON OK!
Continua ad apparire una , in più!!
FStag=c( FStag1[7:12], FStag1[1:6]) # Ordino da gennaio. OK!
FStag=c( FStag1[7:12], FStag1[1:6]) # da controllare! Ordino da gennaio. OK, ora sì
ESAs=rep(FSTAG,5) # EFFETTO STAGIONALE As #Nonostante le correzioni continua a scrivere la variabile FSTAG sbagliata!
ESAs=rep(FStag,5) #OK
ESAs
Yt1=yt-ESAs # Ciclo+Trend+Random
Yt1
Yt1s=as-vector(Yt1s) # smusso Yt1 con Mm 3*3 #Nonostante le varie correzioni appare una – al posto di un .
Yt1s=as.vector(Yt1s) # OK
Yt1s=c()
for(i in 1:60){Yt1s[i]=(Yt1[i-2]+2*Yt1[i-1]+3*Yt1[i]+2*Yt1[i+1]+
Yt1[i+2])/9}
Yt1s # yt1 senza random; cioè Ciclo+Trend
RD=Yt1-Yt1s # forse si tratta solo di random: il Ciclo?
#Riportiamo in una tabella i 5 vettori dell’analisi su yt
#data <- data.frame(t,yt,ESAs,Yt1,RD)
# Facciamo i 5 correlogrammi dei vettori trovati: yt, ESAs, Yt1, Yt1s, RD
coryt=acf(yt)
coryt
corESAs=acf(ESAs)
corESAs
corYt1=acf(Yt1)
corYt1s=acf(Yt1s)
corYt1s
corRD=acf(RD)
# Interessante abbinare il correlogramma con il periodogramma.
ESEMPIO GUIDA IN R SULL’ANALISI DELL’ARSENICO: STAGIONALITA’ TRIMESTRALE
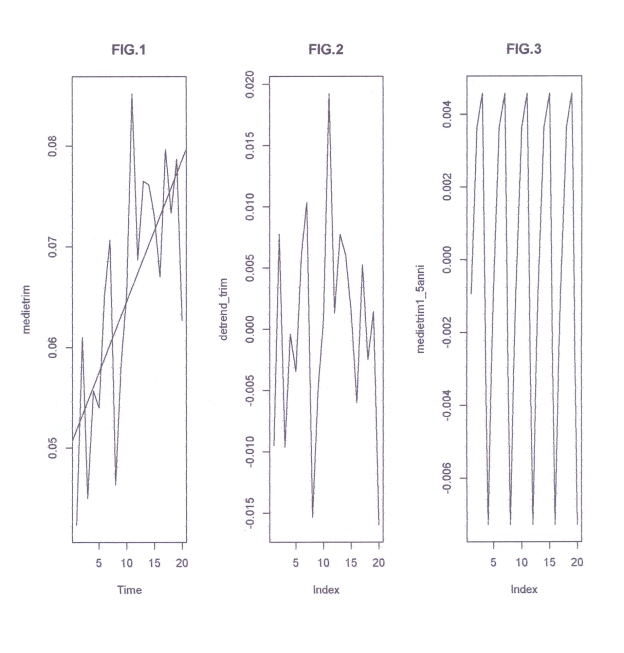
-Ho 60 dati mensili iniziali della concentrazione As delle sorgenti della Carlina (Siena). Col comando (comando in s.l.)) “matrix” organizzo per righe i 60 dati in 20 righe 3 colonne. Col comando “rowMeans” calcolo le 20 medie di riga che sono le medie trimestrali che ho chiamato ‘medietrim’ (FIG.1) che consideriamo come vettore dati da analizzare. Col comando “lm” trovo la retta di regressione sulle 20 medie trimestrali (FIG.1). La retta, pur significativa, non è molto adeguata ai dati; spiega solo il 48% della variazione. Trovo i valori predetti dalla retta con la funzione “predict”. Tolgo i 20 valori predetti dai 20 iniziali ottengo una nuova serie che è quella iniziale senza il trend rettilineo nominata ‘detrend_trim’ (FIG.2); ancora con il comando matrix riorganizzo per riga ‘detrend_trim’ in 5 righe, 4 colonne. Nelle 4 colonne ci vanno i 4 valori trimestrali nell'”anno medio”. Infatti nella prima colonna ho i 5 valori del 1°trimestre dei 5 anni; nella seconda colonna i 5 valori del 2° trimestre e così via. Con il comando “colMeans” faccio le medie di queste 4 colonne ottenendo il Fattore stagionale trimestrale, costituito da 4 termini che estendo ai 5 anni (FIG.3 e Fig.4) con il comando ‘rep’. I 20 dati risultanti costituiscono l’Effetto stagionale. Togliamo ancora dai 20 valori originali (medietrim) l’Effetto Stagionale così ottenuto: ne risulta una nuova serie che è la serie iniziale priva dell’oscillazione stagionale. ma con trend e residui (medieAdj_trim). Su questa serie con “lm” faccio una nuova regressione lineare con aumento dell’R-q fino a 58% (FIG.5), ottenendo come risultato della regressione ‘fitadjtrim. Potrei ottenere ora i residui sottraendo la retta della FIG.5 dai valori plottati. In effetti calcolo i residui col comando “resid” e plotto i residui (FIG.6). Sui residui applico il test di D.-Watson (forse converrebbe interpolare l’elemento 11); applico il comando acf su res (concludo: correlazione assente); osservo infine i 4 grafici finali relativi ai residui ottenuti con plot(fitadj_trim). Conclusione: ritengo l’analisi accettabile!
SCRIPTS IN R
library(graphics)
library(tseries)
library(stats)
library(UsingR)
library(lattice)
library(lmtest)
w=c(0.033,0.043,0.051,0.059,0.061,0.063,0.053,0.036,0.046,0.056,
0.063,0.048,0.053,0.043,0.066,0.053,0.082,0.06,0.08,0.076,0.056,
0.036,0.05,0.053,0.056,0.058,0.061,0.063,0.065,
0.068,0.0815,0.095,0.079,0.063,0.069,0.074,
0.08,0.0765,0.073,0.0695,0.066,0.093,0.083,
0.073,0.063,0.074,0.067,0.06,0.086,0.08,0.073,0.067,0.089,0.064,
0.087,0.079,0.07,0.065,0.06,.063)
par(ask=T)
par(mfrow=c(1,3))
trim=matrix(w,ncol=3,byrow=T)
medietrim=rowMeans(trim)
medietrim
# FIG.1
ts.plot(medietrim,type=”l”,main=”FIG.1″) #finchè non lo sostituisco posso usare abline
w1=c(1:20)
regtrim=lm(medietrim~w1)
abline(regtrim)
summary(regtrim)
val_pred_w=predict(regtrim) #calcolo i 20 valori predetti dalla prima regressione
length(val_pred_w)
detrend_trim=medietrim-val_pred_w
#FIG.2
plot(detrend_trim,type=”l”, main=”FIG.2″)
trim1=matrix(detrend_trim,ncol=4,byrow=T)
medietrim1=colMeans(trim1)
medietrim1_5anni=rep(medietrim1,5)
#FIG.3
plot(medietrim1_5anni,type=”l”,main=”FIG.3″)
par(mfrow=c(2,2))
#FIG.4
acf(medietrim1_5anni,main=”FIG.4″)
valAdjtrim=medietrim-medietrim1_5anni #trend_ random
fitadj_trim=lm(valAdjtrim~w1)
fitadj_trim
summary(fitadj_trim)
#FIG.5
plot(valAdjtrim,type=”l”,main=”FIG.5″)
abline(fitadj_trim)
#ANALISI RESIDUI
dwtest(fitadj_trim, alternative=”two.sided”)
#forse potremo interpolare l’elemento 11
#FIG.6
res=resid(fitadj_trim)
plot(res,type=”l”, main=”FIG.6″)
#FIG.7
acf(res, main=”FIG.7-res”)

par(mfrow=c(2,2))
#FIG.8-12
plot(fitadj_trim, main=”FIG.8-12″)

BLOCCO_NOTE_TRIMAs
ESTENSIONE DELLA PRECEDENTE GUIDA A DIVERSE SERIE STORICHE (dati orari, giornalieri, settimanali, mensili…): BREVI RIFLESSIONI. FATTORI ED EFFETTI STAGIONALI
Si parte da dati orari – Si abbiano dati orari, es., per un anno (n=24*365 dati). Faccio le osservazioni preliminari su questi dati (grafico, correlazione, periodogramma). Con i dati orari possiamo sbizzarrirci. Potrei con matrix organizzare n in una matrice per righe di 24 colonne e 365 righe. Con rowMeans potrei ottenere le 365 medie giornaliere su cui procedere all’analisi di dati mensili: grafico medie, trend, medie meno trend (o meno media): oscillazione+res, su cui applico ancora matrix per riga per ottenere, es., 30 colonne e 12 righe. Che cosa otterrei con rowMeans? Ottengo nella prima riga la media dei primi 30 giorni (media di gennaio), nella seconda la media di febbraio e cosi via fino alla riga 12 che sarà la media di dicembre; in definitiva rowMeans mi fornisce i dodici valori mensili che se si vuole possiamo continuare ad analizzare. Ma ipotizzo ci sia una oscillazione anche all’interno dei 24 dati orari, cioè in un giorno (Fattore stagionale orario). Per questo applichiamo invece ad n iniziale, organizzato in 24 colonne e 360 righe, colMeans. Nella prima colonna ci saranno i 360 valori relativi alle ore una, nella seconda, quelle relativi alle ore 2 … nella 24-esima i dati relativi alle ore 24 di ogni giorno. Ne consegue che colMeans calcola le 24 medie di ogni ora del giorno di tutti i 365 giorni dell’anno in studio (media di 365 valori corrispondenti alle una, alle due…). Questo si chiama Fattore Stagionale relativo alle ore per l’anno in studio. Se volessi il Fattore stagionale mensile? Con matrix dovrei organizzare i 360 dati in 30 righe e 12 colonne. Allora nella prima colonna andranno tutti i primi di ogni mese, nella seconda tutti i due di ogni mese, nella terza i tre di ogni mese e… nella trentesima tutti trenta del mese. Con colMeans troverei il Fattore Stagionale mensile. Per ottenere i relativi Effetti stagionali orari o mensili, ripeto con ‘rep’ rispettivamente i 24 o i 30 valori lungo l’intero anno (365 volte per le ore e 12 volte per i mesi). In generale l’ES, se c’è, si toglie dai dati iniziali, per ottenere una serie nuova senza tale effetto (senza oscillazioni), ma contenente trend+residui. Da questa serie poi si toglie il trend e si studiano i residui per controllare se il nostro processo è sostenibile. Potrei anche cercare il Fattore e l’Effetto stagionale settimanale (365/7= 52 settimane). La grandezza in studio cambia con i giorni della settimana? Per es., gli umani muoiono o fanno l’amore più di lunedi o di sabato? DA RIVEDERE
Link interni curati da Piero Pistoia
1-PERCHE’ RITENIAMO RILEVANTE OGGI UNA COMUNICAZIONE DIDATTICO-OPERATIVA SUL METODO DEI MINIMI QUADRATI APPLICATO ANCHE AD UN POLINOMIO TRIGONOMETRICO
2-BREVE DISCUSSIONE SULL’ ‘ARGOMENTO’ DELLA FUNZIONE SENO
3-USO DELL’ARCO-TANGENTE NEI PROGRAMMI
4-COME ‘FITTARE’ UNA COMBINAZIONE DI FUNZIONI LINEARI AI DATI DI UNA SERIE STORICA.
5-MODELLO DI REGRESSIONE LINEARE SEMPLICE: PRESENTAZIONE E ANTICIPAZIONI NECESSARIE’
6-PRIMA LINEA DI RICERCA NELLA REGRESSIONE LINEARE SEMPLICE
7-COME SI FA A VEDERE SE QUESTO MODELLO LINEARE E’ ACCETTABILE CON R. ANALISI DEI RESIDUI.
8-VARIE INFERENZE STATISTICHE CON R DOPO AVER ACCETTATO IL MODELLO CHE FITTA I DATI
9-COME SI COSTRUISCONO LE BANDE DI CONFIDENZA
10-SCRIPTS DEL PROGRAMMA IN R RELATIVO ALLA REGRESSIONE LINEARE SEMPLICE
11-COME SI FA A VEDERE SE QUESTO MODELLO E’ ACCETTABILE CON IL MATHEMATICA DI WOLFRAN Scripts di Piero Pistoia
1-PERCHE’ RITENIAMO RILEVANTE OGGI UNA COMUNICAZIONE DIDATTICO-OPERATIVA SUL METODO DEI MINIMI QUADRATI APPLICATO ANCHE AD UN POLINOMIO TRIGONOMETRICO
Uno dei problemi oggi della comunicazione culturale scientifica, sia nella Scuola sia nell’extrascolastico, è la settorializzazione continua di linguaggi sempre più evoluti, per descrivere oggetti sempre più complessi e intrisi di teoria (di “spirito” per dirlo nel linguaggio delle monadi di Leibniz). Poiché anche le scelte sociali a cui il cittadino deve essere chiamato a partecipare (se non vogliamo ritrovarci nella situazione dei nuovi analfabeti di G. Holton (1)), sono sempre più condizionate dalle relazioni tecniche degli esperti dei diversi settori, le strutture preposte alla comunicazione dovranno attivarsi per studiare il problema ed individuare i saperi che più di altri siano idonei alle scelte nell’attività sociale. “Libertà è partecipazione”, mutuando l’espressione da una canzone di Gaber, è un concetto che risuona spesso in questi ultimi tempi ora rievocato da alcuni versi di B. Brecht “Controlla il conto sei tu che lo devi pagare”, ora dal “sesto degli undici suggerimenti di un Dio” descritti da G. Conte (2) (“non accettare regole che tu stesso non ti sia dato, non adeguarti mai al pensiero della maggioranza ed alle sue mode, perché l’opinione dei più spesso non è garanzia”…).
La difficoltà incontrata nell’imparare Scienza e nell’assimilarla sembra non dipendere solo da una proposta di insegnamento più o meno efficace o gradevole, ma rimanda alla natura stessa della Scienza, che appare poco congeniale alla biologia delle mente umana (L. Wolpert, 1996 (4), parla di “scienza innaturale”). Sembra esistere cioè una discontinuità profonda fra senso comune e Scienza, con scarsa possibilità di trasferire facilmente cose della scienza al senso e all’intuito comuni e forti difficoltà ad “incarnare” i concetti scientifici. Il cervello dell’Homo sapiens, evolutosi da qualche milione a quarantamila anni fa, in interazione con un ambiente di sopravvivenza “sentito” al fine della caccia e raccolta, mediate attraverso i primi strumenti litici, la prima tecnologia che riusciva a costruire, è progetto di un genoma rimasto, fin da allora pressoché invariato, in eredità alla specie . Infatti a partire da circa 40000 anni fa il cervello umano iniziò a controllare l’evoluzione: invece di continuare a modificarsi con l’ambiente, modificava l’ambiente a sé (evoluzione da biologica a culturale di Dobzansky). Così oggi possediamo pressoché lo stesso cervello del nostro lontano antenato cacciatore raccoglitore e le pulsioni ereditate sono le responsabili delle limitate potenzialità del nostro senso comune non previsto per la comprensione scientifica, ma semmai per una tecnologia sganciata dalla scienza. L’attività scientifica può procedere solo “rompendo” con la conoscenza prescientifica ed il senso comune, come fanno gli animali sagaci di Rilke, che, sagaci appunto ed avventurosi, si sentono a disagio nella situazione pacata e di certezza in cui si trovano. Non si tratta di un prolungamento o raffinamento o ampliamento del senso comune come talora si legge, ma di qualcosa di nuovo: una specie di senso per la comprensione scientifica.. “Finchè la Scuola non fa capire quale spostamento di quadri concettuali è necessario per impadronirsi di alcuni piccoli elementari pilastri della Fisica e della Biologia, la Scuola non ha risposto alle domande a cui dovrebbe rispondere” (P. Rossi, 1996, (5)).
Una possibilità ipotetica di indebolire il senso comune si propone con un approfondimento dei processi di comprensione scientifica in un insegnamento, a livello orizzontale, intensivo e sostenuto dall’uso di una programmazione il più possibile congeniale ai processi della natura (linguaggi come il Mathematica di Wolfram) e, a livello verticale, in un insegnamento a spirale (proposto sia dal primo sia dal secondo Bruner (6)) in più riprese nel tempo. Infatti, come suggerisce la Teoria del Darwnismo Neurale del neurobiologo G. Edelman, 1998 (7), all’interno del cervello sotto la pressione delle argomentazioni collegate alla comprensione dei concetti scientifici, si possono costituire nuovi circuiti cerebrali (selezionando gruppi neurali con l’aprire o chiudere sinapsi), per cui a lungo andare quel pezzo di cultura si “incarna” (senza apportare modifiche al genoma?), innescando però processi intuitivi e creativi con arricchimento del senso comune rispetto all’argomento in studio. Si viene così a favorire quel processo automanico ed inconsapevole (Einfhunlung=immedesimazione) che potrebbe catalizzare ipotesi creative, ovvero indovinare il mondo.
La rapida obsolescenza dei concetti scientifici acquisiti nella scuola, le possibile tendenze riduttive delle nuove riforme che sembrano indirizzare l’insegnamento, in maniera più o meno mediata o camuffata, verso un inserimento più efficace nelle aziende, e la necessità armai stringente nella vita sociale di partecipare in modo sempre più esperto ai progetti e alle decisioni, se non vogliamo diventare cittadini tagliati fuori dalle scelte di sopravvivenza, spingerebbero verso una riformulazione dei curricola scolastici così da includere anche a livelli più bassi di scolarizzazione saperi indispensabili per queste scelte onde innescare l’insegnamento a spirale per facilitarne il trasferimento a livello di senso comune (assimilazione). Parlo dei settori culturali che riguardano per es. l’uso della Statistica, perché con essa scopriremo il profondo e talora ambiguo significato dei “grandi” numeri esprimenti misure (3), ma specialmente dell’analisi dei dati storici, sui quali e solo su essi, sarà possibile costruire oculatamente progetti e previsioni o almeno indicare con una certa probabilità i rischi per i possibili percorsi futuri.
In questo contesto proporremo, insieme a cenni sulle regressioni lineari e multilineari, già oggi oggetto dei corsi di aggiornamento per docenti di materie scientifiche, una riformulazione informatico-operativa dell’analisi di Fourier per insegnanti dell’area scientifica, privilegiando, tramite il Matematica di Wolfram e il linguaggio di R, più che le solite dimostrazioni matematiche, un modo più intuitivo e concreto di affrontare questi concetti.
(1)-Gerald Holton “Scienza, educazione ed interesse pubblico”, il Mulino, 1990.
(2)-Giuseppe Conte “Manuale di poesia” Guanda Editore,1995. pag.26
(3)-Piero Pistoia “Esempi di analisi statistica applicata”, Didattica delle Scienze, n. 180 en. 183. La Scuola, Brescia.
(4)-L. Wolpert “La natura innaturale della Scienza”, 1996, Dedalo editore.
(5)-Paolo Rossi “Intervista”, Le Scienze, aprile, 1996.
(6)-J. Bruner “La cultura dell’Educazione”, 1997, Feltrinelli.
(7)-Gerald Edelman “Darwinismo neurale. La teoria della selezione dei gruppi neuronali”, Einaudi Editore, 1995.
>BREVE DISCUSSIONE SULL’ <<ARGOMENTO>> DELLA FUNZIONE SENO
Si tratta di una breve riflessione sulla funzione seno e sui modi diversi di scrivere il suo argomento con esercitazione al computer (le notazioni usate nello scrivere le funzioni ed i loro argomenti sono quelle proposte dal programma Mathematica), per evidenziare l’influenza di questi modi sulla forma dell’onda e allenare così l’intuito sulle varie questioni, in particolare per gli insegnanti di Scienze.
Un’onda sinusoidale può avere l’espressione generale: yt=A*Sin[K*α+φ], dove alfa varia da 0 a 2π , la costante moltiplicativa K, come si vede, non ha dimensioni e rappresenta il numero delle onde complete in 360° e phi, la fase, rappresenta uno spostamento orizzontale del grafico dell’onda.
se α=0:
per φ=π/2, y=A ampiezza massima dell’onda che parte appunto dal valore max=A, diventando un’onda del coseno a fase zero;
per φ=0, A=0 e l’onda parte da zero;
per φ diverso da 0, caso generale, y=A Sin(φ).
Nel contesto di una serie storica l’eq. precedente acquista una forma leggermente diversa. Chiamiamo n il numero dei dati sperimentali misurati ad intervalli di tempo uguali (serie storica); esso è anche il numero degli intervalli di osservazione e quindi il periodo T della serie (T=n), immaginando che esista almeno un ciclo oscillativo completo in n dati (anche se può non esserci). Allora α/t= 2π/T; α=2πt/T = 2πt/n e yt=A*sin((k/n*t)*2*π+φ). Il simbolo K, talora detto impropriamente frequenza, rappresenta il numero dei cicli completi in n dati sperimentali ed è il numeratore della frequenza: f=K/n. Per vedere che cosa accade delle onde yt quando, per es., n=64 dati, A=1 e k varia da 1 a 3, e t varia da 0 a 64 con φ=0, far girare sul Mathematica di Wolfram (8) il programmino seguente (da aggiustare ai dati), mantenendone con attenzione la struttura e dove con Table si costruisce il vettore Yti dei dati ricavati dalla funzione:
n=64;A=1;
Yti=N[Table[A Sin[(K/n t) 2 Pi],{t,0,64}]], dove a K si sostituiscono prima 1 per ottenere yt (64 valori dell’espressione), poi 2 per ricavare yt1, un vettore dati ancora di numerosità 64, e infine 3 per yt2.
Per graficare questi tre vettori dati: yg=ListPlot[y,PlotJoined->True, GridLines->{Automatic,Automatic}], dove ad y si sostituisce in successione yt, yt1, yt2
Si deve cioè trascrivere sulla console del mathematica (vers. 2.2, 4.1…), le seguenti linee di istruzioni con attenzione (rispettando maiuscole, parentesi e distanze):
n=64;A=1;
K=1 “Si ha un’onda completa in 64 dati T=n”
yt=N[Table[A Sin(K/n t) 2 Pi],{t,0,n}]];
yg=ListPlot[yt,PlotJoined->True,GridLines->{Automatic, Automatic}]
K=2 “Si hanno due onde complete in 64 dati: T=n/2”
yt1=N[Table[A Sin(K/n t) 2 Pi],{t,0,64},{t,0,n}]];
yg1=ListPlot[yt1,PlotJoined->True,GridLines->{Automatic, Automatic}]
ytgg1=Show[yg,yg1] “Le due onde sullo stesso piano cartesiano”
K=3 “Si hanno tre onde complete in 64 dati: T=n/3”
yt2=N[Table[A Sin(K/n t) 2 Pi],{t,0,n}]];
yg2=ListPlot[yt2,PlotJoined->True,GridLines->{Automatic, Automatic}]
ytgg1g2=Show[yg,yg1,yt2] “Le tre onde sullo stesso piano cartesiano (si provi a meccanizzare con un For)”
Proviamo ad ottenere gli stessi risultati col programma R (da elaborare)
Se infine n=64, A=2, k=1 e φ=45°:
yt3=N[Table[2 Sin[(k t 2 Pi)/n+Pi/4],{t,0,n}]]
yg=ListPlot[yt3,PlotJoined->True, GridLines->{Automatic,Automatic}]
Naturalmente ognuno può inventare gli esempi che vuole ed esercitarsi a piacere, una volta acquisita la sintassi di questo linguaggio.
Proviamo ad ottenere gli stessi risultati col programma R (da elaborare)
USO DELL’ARCO-TANGENTE NEI PROGRAMMI
Una precisazione specifica, a nostro avviso rilevante, va fatta sull’uso dell’arcotangente nei programmi, anche perché questi interventi sono rivolti ad insegnanti di Scienze in generale e comunque un insegnamento a “spirale” serve sempre. Per il calcolo delle fasi φ delle armoniche è necessario appunto applicare l’arcotangente al rapporto fra i coefficienti ak e bk di Fourier. L’ArcTan opera sulla tangente di un certo angolo alfa e dovrebbe riportare a video l’angolo di partenza secondo la convenzione standard per la misura degli angoli. In effetti, salvo per alcuni linguaggi con due funzioni ArcTan, una delle quali darebbe il giusto risultato, appare in generale un angolo compreso fra –Pi/2 e +Pi/2 (Pi = π nel linguaggio di Mathematica e pi in quello di R). Salvo il caso in cui alfa alla partenza cade nel 1° quadrante, sul risultato dell’ArcTan in generale dovremo operare alcune correzioni memorizzate nei programmi proposti che vale la pena ricordare. Vediamo come.
Se α alla partenza cadeva nel 2° quadrante (da 90° a 180°), es.97° = 1.69297 rad, la tangente (-8.14435) è negativa (sen + , cos -) e l’ArcTan lo riporta nel 4° quadrante fra –Pi/2 e 0 (cioè: -83°= -1.44862 rad), per cui dovrò aggiungere 180° per avere il valore di partenza nel 2° quadrante (cioè: -83+180=97°).
Se alfa alla partenza era nel 3° quadrante (da 180°a 270°), es. 187°=3.26377 rad, la tangente (.122785) è positiva (sen – e cos -), l’ArcTan lo riporta fra 0 e Pi/2 nel 1° quadrante (7°=.122173 rad), dovrò così aggiungere ancora 180° per riportarlo al quadrante di origine, nel 3°.
Se alfa era nel 4°, es. 280°=4.88692 rad con tangente -5.671282, cioè negativa (sen -, cos +), l’ArcTan riporta un valore fra –Pi/2 e 0 (cioè: -80°= -1.39626 rad); dovrò così aggiungere a -80, 360 per avere i 280° di partenza.
Precisiamo infine i seguenti casi particolari. Se la tangente è zero (angolo di partenza 0 o 180°, seno=0 e coseno diverso da0 imponiamo che l’ArcTan sia zero. Se l’angolo di partenza è 90 ovvero 270° (seno +1 o –1 e coseno 0), imponiamo che l’ArcTan sia rispettivamente 90° o –90° (-90+360). Se infine ak=0 e bk=0, caso frequente nell’analisi di Fourier quando certe armoniche sono assenti nei dati, imponiamo che ArcTan sia 0°. vedere le istruzioni di R per portare phi al quadrante giusto.
4-COME ‘FITTARE’ UNA COMBINAZIONE DI FUNZIONI LINEARI AI DATI DI UNA SERIE STORICA.
Regressione lineare semplice, Algebra matriciale per regressioni anche Multilineari e matrice inversa con esempi di calcolo (vedere sul blog)
MODELLO DI REGRESSIONE LINEARE SEMPLICE: PRESENTAZIONE E ANTICIPAZIONI NECESSARIE
Il punto essenziale non è tanto quello di trattare teoricamente il metodo dei minimi quadrati (aspetto culturale abbastanza scontato), ma di prendere piena consapevolezza che tale metodo è applicabile a qualsiasi nube di punti, al limite anche omogeneamente distribuiti nel piano cartesiano, e che fornisce in ogni caso risultati! Diventa necessario e quindi obbligatorio in una ricerca seria valutare quanto questo modello sia valido di fatto (F. Anscombe,1973 ” Graphics Statistical Analysis”, American Statistician 27(1).
Secondo noi, esistono tre linee di ricerca nell’affrontare i problemi posti dai modelli di regressione.
1- La prima linea di ricerca, minimi quadrati s.s., ci permette di capire quanto il modello ‘fitta’ bene i dati sperimentali, cioè si adatta bene ad essi (la specifica grandezza calcolata è R-quadro, quadrato del Coefficiente di Correlazione, fra l’altro (vedere dopo), fra yi, variabile dipendente e xi indipendente.
2- La seconda linea di ricerca, una volta soddisfatti dell’adeguatezza della retta ai dati sperimentali, ci dobbiamo mettere nelle condizioni di poter ‘misurare statisticamente ‘ anche l’adeguatezza di quella retta sperimentale all’ipotetica retta tracciata nell’Universo di tutti i campioni possibili. In un’analisi sulla retta di regressione, è necessario che vengano rispettate una serie di ipotesi relative alle Yi della popolazione da cui proviene il campione, come 1) valori normali : cioè per ogni Xi la distribuzione degli Yi è una gaussiana; per ogni valore cioè di Xi nell’Universo esisterà nella terza dimensione una gaussiana, le cui ascisse si trovano lungo la retta passante per Xi,Yi* parallela all’asse Y. 2) Uguali varianze (omoscedasticità: le distribuzioni gaussiane di Yi, di cui al punto 1, devono avere uguale varianza.. 3) Linearità: le medie di tutte queste distribuzioni di Yi con uguale varianza, per ogni Xi, dovranno cadere sulla retta di regressione teorica. 4) Indipendenza: tutte le osservazioni devono essere indipendenti nel senso che i valori di un dato non devono influenzare gli altri. Non ci devono essere cioè altre relazioni causali all’interno dei dati eccetto quella espressa dalla retta di regressione.
Per controllare tutte queste ipotesi necessarie al modello relative agli Xi,Yi della popolazione universo si opera a posteriori sui RESIDUI che si possono misurare essendo stime degli ‘errori veri’ (Yi-Yi*). Ciò che resta dopo aver ‘fittato’ un qualsiasi modello, si dice residuo, per ogni xi, la differenza fra i valori yri sulla retta sperimentale (da essa predetti) ed i corrispondenti osservati o misurati della variabile dipendente yi; residuo è quello che il modello non spiega. Queste ipotesi elencate sulla variabile dipendente della popolazione universo si riflettono direttamente sugli εi che a loro volta agiscono sui residui che dovranno avere in qualche modo lo stesso comportamento che può essere misurato. Quindi i livelli di significanza, gli intervalli di confidenza e gli altri tests sulla regressione sono sensibili a certi tipi di violazione dei residui e non possono essere interpretati nell’usuale modo, se esistono serie discrepanze nelle assunzioni e quindi sui residui.
In un’analisi della regressione gli εi si pensano, come già accenato, come 1) normali, 2)indipendenti, 3)con media zero e 4)varianza, sigmo-quadro, costante. Se il modello è appropriato, i residui osservati, che sono stime degli errori veri, dovrebbero avere simili caratteristiche.
I valori dei residui (resi) si stimano meglio se ogni residuo viene diviso per la stima della deviazione standard dei residui con N-1 al denominatore del radicando, ottenendo così la serie dei residui standardizzati. I residui standardizzati con media zero e deviazione standard 1, sono valori positivi, se sopra la media, e valori negativi se sotto la media. Così dire che un residuo è per es., -4721, ci fornisce poca informazione; se invece la sua forma standardizzata è -3.1, ciò ci suggerisce subito non solo che il valore osservato è minore di quello predetto, ma anche che quel residuo è certamente maggiore in valore assoluto alla maggior parte dei residui, essendo più di tre deviazioni standard.
Vedere nel proseguio l’utilizzo di grafici opportuni ed altri tests (correlogramma, periodogramma, test di DURBIN_WATSON e gli svariati tests per la normalità) per valutare se la nostra curva sperimentale permette, tramite l’analisi dei residui di passare al punto 3 onde fare inferenze statistiche dal campione alla popolazione sui parametri teorici del modello, intervalli di confidenza e bande di confidenza. Da notare con attenzione che prima di aver fatto l’analisi dei residui i processi di calcolo di cui al punto 1 che rimandano alla popolazione (ottenuti come outputs di programmi al computer o altro) devono essere lasciati in sospeso! A meno che, come avviene di fatto in generale, decidiamo di procedere, senza porci problemi, a ‘testare’ le nostre ipotesi sul comportamento della popolazione, tenendo presente che le nostre conclusioni saranno affidabili o meno secondo ciò che ricaviamo dall’analisi dei residui. Infatti Anscombe nel 1973 dimostrò con i suoi campioni fittizi che due serie di dati diversi, sottoposti a regressione lineare anche se danno stessi risultati (dai coefficienti della retta alle loro inferenze sulla popolazione tramite la statistica t, all’ R-quadro e sua l’inferenza tramite la statistica F e tutte le altre conclusioni inferenziali) e non essere un modello adeguato se non sono rispettate le assunzioni sui residui standardizzati N(0, sigma^2) compresa l’indipendenza.
3- Terza linea di ricerca. Comunque sia, se dopo l’analisi dei residui accettiamo il modello, siamo in grado, come vedremo, di fare inferenze verso la popolazione circa tutti i parametri teorici del modello oppure accettare quelle già fatte
PRIMA LINEA DI RICERCA NELLA REGRESSIONE LINEARE SEMPLICE. Un possibile racconto.
Iniziamo misurando o utilizzando N coppie di dati (xi,yi) relativi a due variabili sperimentali, che nel piano cartesiano x,y ipotizziamo statisticamente distribuiti come una retta (ipotesi suggerita dal grafico cartesiano o da altro) per cui sia applicabile il seguente modello matematico:
Yi* = β0 + β1 * xi + εi ; (xi,Yi*) sono le coordinate di n punti sulla retta nella popolazione, mentre (xi,yi) sono le n coppie dei punti sperimentali.
dove xi è l’ascissa di ogni punto sperimentale e yr è l’ordinata corrispondente sulla retta di regressione, mentre xi,yi corrispondono ai punti sperimentali; εi, sconosciuti, rappresentano quanto Yi* differisce da Yi nella popolazione. Se conoscessi gli εi troverei i coefficienti β0 e β1 teorici.
Se non conosciamo gli εi, riscriviamo il modello sostituendo i corrispondenti valori stimati a e b ( o b0 e b1) che riassumono gli εi
yi = a + b * xi: si tratta di scrivere n equazioni sostituendo le coppie di valori conosciuti a xi e yi. Trovati a e b, ricaverò yr, “ordinate fittate”, (yr=a+bxi) ; allora yr*-Yr =εi che è la quantità residua dell’iesima osservazione; mentre resi=yr-yi -> residui. Notare la differenza fra yi e yr .
dove xi,yi sono ancora le coppie di dati sperimentali, yr sono i valori sulla retta di regressione che ricaverò con i minimi quadrati e i valori beta0 (β0) e beta1 (β1) invece devono essere stimati e calcolati dalle coppie (xi,yi) conosciute e indicati con a e b1 o b0 e b1, che rappresentano le nostre incognite. Per stimare beta0 e beta1, cioè calcolare le loro stime (a e b o b0 e b1)) dato che non conosciamo gli εi, è necessario individuare in qualche modo una particolare retta tracciata attraverso i punti (xi,yi) segnati nel piano cartesiano. Ma in quanti modi possiamo tracciare questa retta? In infiniti modi! E’ necessario quindi formulare un’ipotesi per individuarla. Ecco l’ipotesi: la somma delle ‘distanze’ elevate al quadrato, misurate lungo l’asse y, fra ogni punto sperimentale (tanti quanto imax) ed il corrispondente sulla retta sia un minimo (metodo dei minimi quadrati). Tali distanze sono appunto i residui (resi) che corrispondono alle stime degli εi. Dobbiamo cioè minimizzare l’espressione seguente: (vedremo poi come):
Σ(yr-yi)^2 = Σ((a + b * xi)-yi)^2 o anche Σ(resi)^2 -> minimo
Le ipotesi iniziali su εi sono Σεi=0, cioè media(εi)=0, distribuzione gaussiana con varianza di εi=σ^2 costante e gli εi, uniformemente distribuiti (senza correlazioni interne). Se avessimo ottenuto una retta di regressione esatta, gli errori εi ed i residui sarebbero la stessa cosa; così ci aspettiamo che i residui ci dicano qualcosa sul valore di σ.
Potevamo anche scegliere altre ipotesi alternative, come per es., considerare la distanza a novanta gradi sempre al quadrato ecc.. Questo metodo consiste quindi nel trovare le stime di beta0 e beta1, cioè a e b, che forniscano come somma delle loro differenze elevate al quadrato un valore più piccolo possibile, cioè Σi (resi ^2)=un minimo. (da rivedere). Facendo i conti con algebra diretta e con programmi (vedere nel proseguio) otteniamo le due equazioni seguenti per il calcolo di queste stime b0 e b1 (o a=b0; b=b1):
b1 = Σi ((xi-xm)*(yi-ym))/Σi (xi-xm)^2 se x =xi-xm e y=yi-ym si può scrivere anche come:
b1=ΣΣ xy / ΣΣ x^2 bi è anche uguale a b1=(nΣxy-ΣxΣy)/(nΣx^2-(Σx)^2) dove. x=xi-xm); y=yi-ym; Σx^2=Sxq=Σ(xi-xm)^2; (Σx)^2=qSx=(Σ(xi-xm))^2
ym = b0 + b1 * xm
Inseriti in qualche programma (vedere dopo) i vettori y e x (per es., i valori della matrice y (dimensioni:60*1) e x (dim.:60*2) nel programma in qbasic allegato (MULTIREG), si ottengono direttamente b0 e b1.
Ora b0 e b1 sono di certo le migliori stime per le corrispondenti grandezze nella popolazione, anche se difficilmente i numeri saranno gli stessi.
R-QUADRO O COEFFICIENTE DI DETERMINAZIONE
Esiste una misura che che indica la bontà di adattamento del modello ai dati sperimentali del campione (xi,yi) che è il Coefficiente di Determinazione indicato con R-quadro, che corrisponde poi al quadrato del Coefficiente di Correlazione lineare di Pearson fra i valori della variabile dipendente yi e la variabile indipendente xi, o fra le yi dei dati e il corrispondente valore sulla retta di regressione yr la cui formula è:
R=Σ(x-xm)(y.ym)/(N-1)SxSy dove Sx ed Sy sono le deviazioni standard delle variabili x e y e n è la numerosità del campione.
R-quadro, come abbiamo già detto, potrebbe essere interpretato anche come il quadrato del coefficiente di correlazione fra yi e yr, valore predetto di y dalla regressione (questa definizione è applicabile direttamente al calcolo di esso nella multiregressione lineare)
Per approfondire il significato di R-quadro calcoliamo quale proporzione della variabilità totale della y può essere ‘spiegata’ dalla x (cioè da modello). La variabilità totale della variabile dipendente (y), cioè yi – ym può essere divisa in due componenti: variabilità spiegata dalla regressione (yri- ym) e non spiegata yi-yri=resi=ei.
yi – ym = (yri- ym) + yi-yri
Elevando a quadrato i due membri (sopprimendo il doppio prodotto che è zero) e applicando l’operatore sommatoria , avremo:
Σ(yi – ym)^2 = Σ(yi-yri)^2 + Σ(yri- ym)^2
che si legge: la somma totale dei quadrati (TOTAL SUM OF SQUARE = TSS) è uguale alla somma dei quadrati residuali (RESIDUAL SUM OF SQUARE = RESS) più la somma dei quadrati di regressione (REGRESSION SUM OF SQUARE = REGSS). Dividendo le sommatorie a destra per i rispettivi gradi di libertà (n-p-1 e p, dove p è il numero delle variabili indipendenti, 1 nel nostro caso) si ottengono la MEAN SQUARE RESIDUAL (MSRES) e la MEAN SQUARE REGRESSION (MSREG), la cui somma è la TOTAL MEAN SQUARE (TMS)
Per calcolare quale proporzione della variabilità totale è spiegata dalla regressione, basta dividere la somma dei quadrati di regressione per la somma dei quadrati totale.
Variazione relativa spiegata = Σ(yri-ym)^2 / Σ(yi-ym)^2
Ci accorgiamo che questo rapporto è uguale a R-quadro (dimostrare). Un R-quadro, per es., di 0.44 significherà che la retta di regressione spiega il 44% della variabilità di y. Se tutte le osservazioni cadono sulla linea di regressione R-quadro è 1. Se non vi è nessuna relazione lineare fra x e y, R-quadro è zero.
Dividendo REGSS e RESS per i rispettivi gradi di libertà (p e n-p-1, dove p è il numero delle variabili indipendenti) si ottengono la MEAN SQUARE RESIDUAL (MSRES) e la MEAN SQUARE REGRESSION (MSREG), la cui somma è la TOTAL MEAN SQUARE (TMS).
Se le assunzioni sono rispettate e sotto le condizioni che R-quadro pop.=0 (assenza di relazione lineare nella popolazione), il rapporto fra MSREG/MSRES è distribuito come la F di Fischer con p e n-p-1 gl. Se tale rapporto è elevato (variazione spiegata > variazione residuale), riportato sulla distribuzione di Fisher, cade nella zona proibita, l’ipotesi che r-quadro pop.=0 deve essere respinta.
COME SI FA A VEDERE SE QUESTO MODELLO LINEARE E’ ACCETTABILE CON R. ANALISI DEI RESIDUI. Uso dei comandi di R.
Seguiamo il processo di costruzione del programma in R. Dobbiamo avere i dati cioè il vettore x=c(x1,x2…xn) e il corrispondente y=c(y1,y2…yn). Facciamo il plot dei dati con
plot(x,y). Da notare che y nell’esempio è chiamato yt.
Cerchiamo con R i risultati della regressione, resultreg, usando i comandi lm(y~x) o simple.lm(x,y) (per quest’ultima caricare il package UsingR)
resultreg=lm(y~x) # o
resultreg=simple.lm(x,t) # usando UsingR
Aggiungiamo al plot la retta di regressione per precisare l’idea sull’ipotesi iniziale (scelta di una regressione lineare semplice), con
abline(lm(y~x))
Nell’oggetto ‘resultreg’ ci sono contenute tutte le informazioni della regressione, in forma matriciale: oltre alle indicazioni dei coefficienti, nella prima colonna si trovano le loro stime, nella seconda i relativi errori standard (SEb0, per l’intercetta e SEb1, per la pendenza, nella quarta i valori della statistica t di Student calcolabile dal campione (b0/SEb0, b1/SEb1) che ci permette di affermare se sono accettabili o meno le stime e nella quinta le probabilità che indicano dove cade ogni stima nella distribuzione di Student. Questi valori possono essere richiamati con coef(summary(resultreg))[1,1] per b1; [2,2] per SE_pensenza ecc. Al di sotto di questa matrice a 2 righe e 4 colonne appaiono il Residual Standard Error (RSE), l’R-quadro e la F di Fisher, richiamabili con il comando cefficients$r-quadro ecc. La grandezza R-quadro (coefficiente di determinazione) e il residual standard error (SE o RSE) misurano l’adeguatezza ai dati (per es., se R^2=0.44, significa che la retta di regressione spiega il 44% della variabilità di yi). Solo dopo l’analisi dei residui valuteremo se tali stime sono accettabili.
summary(resultreg) #riassume quasi tutti i dettagli.
Per vedere parti di tali informazioni si usano i comandi res(resultreg); coef(resultreg); predict(resultreg)
b0=coef(summary(resultreg))[1,1]
b0
b1=coef(summary(resultreg))[2,1]
b1
SEb1=coef(summary(resultreg))[2,2]
SEb1
SEb0=coef(summary(resultreg))[1,2]
SEb0
summary(res) fornisce: min. 1° Quantile, Mediana, Media, 3° Quantile, max, sui residui
Una volta conosciuto, interpretando le informazioni contenute in resultreg, che il modello è appropriato ai dati (fitta bene i dati), è necessario analizzare se sono rispettate le ipotesi iniziali sui residui che rimandano alla validità del modello. Successivamente vedremo come si comporteranno i parametri incogniti, stimati dai dati, nella popolazione da cui viene estratto il campione.
Nel prosieguo ricalcoleremo tutte queste grandezze usando comandi di più basso livello.
COME TESTARE I RESIDUI
Per vedere se vengono rispettate le assunzioni di linearità, cioè se davvero una linea retta ‘fitta’ bene i dati, e l’omogeneità della varianza (OMOSCEDASTICITA’), si possono plottare i residui (y) contro i valori predetti dalla regressione (x). Se si presentano chiari patterns nei grafici detti, tali assunzioni possono essere violate. In un grafico fra valori predetti standardizzati (asse x) e residui standardizzati, i residui infatti dovrebbero essere distribuiti casualmente in una banda diffusa intorno ad una linea orizzontale, che passa per lo zero. Altre configurazioni di fasce dello stesso spessore più o meno piegate prevedono assenza di lineatità. Se invece è lo sparpagliamento dei residui ad aumentare o diminuire con la variabile x o con i valori predetti, probabilmente l’assunzione di omoscedasticità non è rispettata. Altro modo efficace per testare l’omoscedasticità dei residui è quella di plottare i residui in funzione di ogni unità di tempo (per es., residui con i mesi, se si presentano patterns a imbuto, a clessidra, a farfalla… si prevede eteroscedasticità. Per controllare infine l’indipendenza dei residui si può osservare il correlogramma e somministrare il test di Durbin-Watson, contenuti insieme ad altro nel programma in Qbasic CORR (scritto da uno degli autori) allegato. Per testare la normalità dei residui possiamo usare svariati tests (chi-quadro, Kolmogorov e Smirnov..o il più recente Lim-Mudholkar (1980), inserito nel programma CORR.
ALTRO ANCORA SUI RESIDUI CON R (da precisare):
1) Per la normalità si possono usare anche istogrammi, boxplot, plots normali; Con Normal qqplot: i residui sono normali se il grafico rimane vicino alla linea.
2) La loro uniforme distribuzione spaziale (random, assenza di correlazione interna o trends), con plots dei residui VS tempo o ordinate;
3) costanza della loro varianza ad ogni xi, con plots dei residui VS tempo, ordinate yi e valori fittati;
con Residual VS fitted: si osserva la diffusione intorno alla retta y=0 e il trend.
Il comando plot farà molto di questo per noi se gli forniamo i risultati della regressione (resultreg):
plot(resultreg) #plotta quattro grafici separati o su un solo piano cartesiano (se esplicitiamo il comando par(mfrow(2,2)).
SEGUE LA DESCRIZIONE DI QUESTI 4 GRAFICI ……GRAFICI RELATIVI ALL’ANALISI DEI RESIDUI IN R
Il comando plot(resultreg) plotta 4 grafici separati oppure sullo stesso piano cartesiano, se esplicitiamo il comando par(mfrow(2,2)).
– Per la normalità dei residui si possono usare anche istogrammi, boxplot e plots normali; con normal qqplot i residui saranno considerati normali se il grafico rimane vicino alla linea tratteggiata (vedere fig. Normal Q-Q). Osserviamo nella curva Normal Q-Q se i residui sono aggruppati e si allontanano dalla riga tratteggiata. Plottiamo le statistiche di ordine del campione ( standardized residuals) vs i quantili da una distribuzione normale norm(mean=0, sd=1) con il comando plot(resultreg, which=2). Possiamo testare la normalità anche con lo Shapiro-Will test:
shapiro.test(residuals(resultreg))
Se il p-value fornito è < di 0.05 significance level, si respinge l’ipotesi nulla H°, che i residui siano normalmente distribuiti. Da notare che il modello di regressione è robusto rispetto all’ipotesi di normalità. Sono più importanti le assunzioni di indipendenza e varianza costante.
– L’ipotesi di indipendenza dei residui è uno dei più importanti. La dipendenza si mostra nell’autocorrelazione che può essere positiva o negativa. Si testa la loro uniforme distribuzione spaziale (random, assenza di correlazione interna o trends), con plots dei residui vs tempo o fitted values. Valori positivi dei residui sono seguiti da valori positivi e valori negativi da valori negativi. Si presenta così un aspetto ciclico nei residui (Fig. Residuals vs fitted).
Si fornisce anche un test statistico, il test di Durbin-Watson, la cui statistica D è calcolata anche dal programma in Qbasic CORR allegato, insieme alla tabella e spiegazione. Con R si fa un test a due lati con l’ipotesi nulla che la correlazione non sia zero. Se il p-value è superiore a, per es., 0.05 di livello di confidenza, si respinge l’ipotesi che non sia zero la correlazione (c’è correlazione).
library(lmtest)
dwtest(resultreg, alternative=”two.sided”)
– La costanza della loro varianza ad ogni xi si usano grafici residui vs tempo, ordinate yi e valori fittati. Con Residuals vs fitted: si osservano la diffusione intorno alla retta y=0 e il trend (vedere fig. Residuals vs fitted). La Fig. Scale Location riporta sulle ordinate la radice quadrata dei residui standardizzati vs fitted value e controlla anch’esso se la la varianza è costante. In generale si dimostra che la varianza dei residui cambia con i residui stessi, per cui conviene dividere ogni residuo per il suo errore standard (Residual Standard Error=radice della varianza = S*sqrt(1-hii)), ottenendo gli standardized residuals. Se resi sono tutti i residui, i residui standardizzati saranno: Rsi=resi/S*sqrt(1-hii) con i da 1 a n, dove hii, chiamata leverage, verrà definita più avanti. Se |Rsi! > 2 questo residuo rimanda ad un valore di y outlier. Cancelliamo da yt questo i-esimo e rifacciamo la regressione con gli n-1 dati, ottenendo un valore fittato Yr(i) senza il residuo Di=y(i)-Yri. Per cui: Var(Di) = S^2(i)/1-hii) e ti = Di/(S(i)/1-hii))
e i ti rappresentano i residui studentizzati cancellati. ti ha una distribuzione t con n-3 gl; riportiamo questi valori su tale distribuzione per decidere se si tratta di un outlier.
Ci aspettiamo una banda costante orizzontale con i fitted value, senza sventagliate in fuori o in dentro.
Tutto questo può essere fatto fare ad R (J. Kerns 2010, Cap.11)</i)
Forniamo tramite comandi di R infine un test statistico (il Breusch Pagan test) ancora per la costanza della varianza, senza entrare nel merito (per questo vedere “Introduction to Probability and Statistics Using R” di G.J. Kerns (prima ed.,pag. 270, prec. e seg.):
library(lmtest))
bptest(resultreg)
Si respingerà l’ipotesi nulla se BP ha un p-value che risulta superiore al livello di confidenza fissato (es., 0.05).
– Fig. Residual vs Leverage – Coinvolge Outliers, Leverage, Distanza di Cook (da elaborare)
8-VARIE INFERENZE STATISTICHE CON R DOPO AVER ACCETTATO IL MODELLO CHE FITTA I DATI
Stime sulle grandezze della popolazione
Procediamo a fare le nostre inferenze a partire dal campione senza preoccuparci per ora delle assunzioni iniziali.
– Si possono così fare stime puntuali, se stimo il valore di un parametro della popolazione a partire dal campione, che possono essere considerate le migliori ipotesi singole immediate per una grandezza della popolazione
– si possono inferire valori degli errori standard dei coefficienti della retta, immaginando di estrarre moltissimi campioni dalla popolazione e calcolare per ognuno il parametro oggetto di inferenza; se le assunzioni sono rispettate, la distribuzione del parametro sarà gaussiana con media corrispondente al valore di quel parametro nella popolazione. Seguono le formule per il calcolo della stima dell’errore standard della pendenza b1 e della stima della varianza della popolazione, costante per ogni x:
SEb1=σβ1=σ/(sqrt((n-1)*Sx^2)) e σ^2=S^2=Σ(yi-(b0+b1*x))^2/(n-2) Da notare che SEb1 stima σβ1
SEb1=S/sqrt((Σ((xi-xm)^2; Sx=standard deviation di x
S stima σ
la cui radice quadrata è l’errore standard della stima o deviazione standard dei residui.
– Spesso basandoci su grandezze del campione, è possibile calcolare un range di valori (centrato sul valore campionario), che, con una fissata probabilità include il valore della grandezza corrispondente nella popolazione. un tale range è detto INTERVALLO DI CONFIDENZA e la stima, stima per intervallo. E’ possibile calcolare un intervallo di confidenza per i valori della popolazione: per es., un intervallo di confidenza al 95% ancora per la pendenza β1:
b1 ± tscore*SEb1 dove ± tscore sono i due valori critici della t di Student, per n-2 gl e, per es.,significanza 0.05 o Intervallo di confidenza al 95%, (in generale se gl>30 la t di Student tende ad una gaussiana per cui tscore è circa 1.96). Così β1 sarà compreso fra b1-1.96*SEb1 e B1+1.96*SEb1 e β0 sarà compreso fra b0-1.96*SEb0 e b0+1.96*SEb0.
Con R: confint(resulreg, level=.95)
Un intervallo di confidenza al 95% significa che noi estraiamo campioni ripetuti da una popolazione, sotto le stesse condizioni, e computiamo per ognuno l’intervallo di confidenza al 95% per la pendenza di quel campione, il 95% di questi intervalli includerebbero il valore sconosciuto della pendenza della popolazione. Naturalmente, poichè i valori veri della popolazione non sono conosciuti, non sapremo mai se quel particolare intervallo lo contenga. Da notare che se nell’intervallo di confidenza per la pendenza non si trova lo zero, significherà che dovremo respingere l’ipotesi nulla che la pendenza sia zero a livello di significanza osservato dello 0.05 o meno.
– Si possono testare ipotesi che un parametro abbia un determinato valore nella popolazione: per es., β1=0 (β1 pendenza della popolazione) o R-quadro nella pop. = 0: nessuna relazione lineare. La stima dell’errore standard della pendenza b1, per esempio, può servire per testare la seguente ipotesi: il valore della pendenza nella popolazione è zero (β1=0)? Può esserlo infatti nella popolazione e non nel campione. Se nella popolazione non esiste relazione lineare (β1=0), si conosce la distribuzione della statistica t=pendenza/errore standard della pendenza, calcolata su tutti i campioni estratti dalla popolazione: si tratta di una distribuzione di Student non n-2 gl. Se il valore del t del nostro campione (tc=b1/SEb1), inserito sulle ascisse di questa distribuzione campionaria dà livelli di significanza (lascia a destra un’area di probabilità inferiore ad una soglia prefissata (0.05,0.01…), allora l’ipotesi nulla (β1=0 nella popolazione) è da respingere e ci sarà effettivamente relazione lineare fra le due variabili nella popolazione. Tale prova però non ci fornisce informazioni relative a quanto la retta di regressione spieghi i dati effettivamente (lo fa, come si è visto in precedenza, R-quadro).
– Come si è visto la somma totale dei quadrati (total sum of squares=TSS) è uguale alla somma dei quadrati residuali (residual sum of squares=RESSS) più la somma dei quadrati di regressione (regression sum of squares=REGSS).
Sotto le condizioni che R-quadro pop.=0 (assenza di relazione lineare nella popolazione), il rapporto fra MSREG/MSRES è distribuito come la F di Fischer con p e n-p-1 gl. Se tale rapporto elevato (variazione spiegata > variazione residuale), riportato sulla distribuzione di Fisher, cade nella zona proibita, l’ipotesi che r-quadro pop.=0 deve essere respinta..
– Si possono così fare controlli incrociati: usando la statistica b1/SE, se non si può respingere l’ipotesi nulla: b1=0: ma allora l’intervallo di confidenza dovrà contenere lo zero; e la F di Fisher non sarà significativa, cioè R-quadro della popolazione=0 ecc..
Inferenza circa σ
Abbiamo due parametri a e b (o b0 e b1) ìricavati dai dati attraverso conti o programmi, tre parametri da stimare nel modello che sono σ, β0 e β1; σ, è la deviazione standard dei termini dell’errore; se avessimo una linea di regressione ‘esatta’ i termini dell’errore ed i residui coinciderebbbero. Invece quello che è vero è che σ deve essere stimato da:
S^2=Σ(yr – yi)^2/(n-2)=Σei^2/(n-2)
dove ei sono i residui. S^2 è uno stimatore unbiased di σ^2, cioè la sua distribuzione campionaria ha come media σ^2 della popolazione universo. E’ la divisione per n-2 che lo rende corretto. La radice positiva di S^2 è chiamata SEE standard error della stima o deviazione standard dei residui. Gi errori standard della pendenza e della intercetta sono stati calcolati da R nella seconda colonna dei risultati.
LO STANDARD ERROR DI b0
σb0=σ*sqrt(1/n + (xm^2/(n-1)*(S_x)^2)
dove (S_x)^2 è la varianza campionaria della variabile indipendente
delta2=(xi-mean(xi))^2
Sx2=sum((xi-mean(xi))^2)/(n-1) varianza campionaria di x
Se sostituisco Sx2 in (S_x)^2, ottengo:
SEb0=S*sqrt(1/n+(mean(xi))^2/Sx2)
LO STANDARD ERROR DI b1
σb1=σ/sqrt((n-1)*(Sx)^2)
PRECISIAMO ALCUNI PASSAGGI
Inferenza circa β1
R include il test per β1=0 che controlla l’ipotesi nulla (nessuna pendenza)
Lo stimatore b1 di β1,cioè la pendenza della linea di regressione nella popolazione, è pure uno stimatore unbiased (corretto, imparziale obbiettivo).
Lo standard error di b1 è:
SEb1=S/(SQRT(Σ(xi-xm)^2) dove S è la radice dello stimatore precedente
PER TESTARE IPOTESI
La distribuzione del valore normalizzato di b1, cioè la sua distribuzione campionaria è una statistica t::
Non vi è alcuna relazione lineare fra x e y quando la pendenza della linea di regressione è 0.
Il test usato è:
t=b1/Sb1 la sua distribuzione statistica quando le assunzioni sono rispettate e l’ipotesi non è una relazione lineare e la distribuzione di Studente con n-2 gl (degree of fredom)
Il test usato per testare l’ipotesi che l’intercetta è zero è:
t=b1/s(b0) ha la stessa distribuzione campionaria.
Queste statistiche t e i loro livelli di significanza a due code sono riportati nella matrice dei risultati R nelle ultime due colonne.
Se vogliamo testare se β1=certo valore si utilizzano le distribuzioni campionarie seguenti:
t=(b1- β1)/SEb1 che ha una distribuzione campionaria t di Student con n-2 gradi di libertà
t=(b0-β0)/SEb0
dove SEb0=S*(sqrt(sum(xi^2/n*sum(xi-xm)^2
A questo punto è facile fare un test di ipotesi per la pendenza della regressione lineare. Per es., se l’ipotesi nulla è H0: β1=w contro l’ipotesi alternativa Ha: β1≠w; allora si può calcolare la statistica campionaria t=(b1-w)/SEb1 e trovare il valore di probabilità corrispondente dalla distribuzione-t.
Si voglia fare un test per vedere se la pendenza di -1 che prevediamo è corretta. Procediamo con R nel test statistico.
>e=resid(resultreg) # i residui del modello resultreg
>b1=(coef(resultreg))[[‘x’]] #la parte x dei coefficienti
>S=sqrt(sum(e^2/(n-2))
>SEb1=S/sum((x-mean(xi))^2 dove x è il vettore dei valori
>t=(b1-(-1))/SEb1 # cioè +1: valore della statistica campionaria
>pt(t,gl,lower.tail=F) #trova la coda a destra per questo valore di t con n-2 gl
Il valore ottenuto raddoppia se il problema richiede due lati. Se la probabilità è inf., es. 0.005 ad un dato valore si respinge l’ipotesi che la pendenza =-1.
Nel comando summary R fa da solo il test per l’ipotesi β1=0 nella colonna (pr(>|t!)) alla posizione 2,4.
Inferenza circa β0= w in R
SE(bo)=S*sqrt(sum(x^2)/n*sum(x.mean(x))^2)))
t=(bo-w)/SEb0 # coef(resultreg)[[‘(intercept)’]]
pt(t,13,lower.tail=TRUE) # la coda inferiore <w
COME SI COSTRUISCONO LE BANDE DI CONFIDENZA
Le bande di confidenza sono strisce lungo la retta di regressione che hanno un buon effetto visivo. La retta di regressione è usata per predire, per ogni x, il valore di yo il valore medio di y. Quanto è accurata questa previsione? prevedere per ogni x un y o la media di y porta a due bande diverse. Il valore medio di y è soggetto ad una variabilità minore della previsione del singolo y. Ambedue gli intervalli sono del tipo
b0+b1*xi ± t* SEprevisione
L’errore standard per la previsione del valore medio di y per un dato xi è:
SEprevym=S*sqrt(1/n + (xi-xmi)^2/(sum(xi-xim)^2)) dove S è la deviazione standard campionaria dei residui ei (RSE).
Se stiamo invece tentando di predire un singolo valore yt allora SEprevyt cambia anche se solo leggermente e in funzione della numerosità:
SEprevyt = S*sqrt(1 + 1/n + (xi-xmi)^2/(sum(xi-xmi)^2))
Basta costruire una tabella a tre colonne per ciascuna previsione (prevym, prevyt). Per es., per prevym: yt, SEprevymlow, SEprevytup. Nella prima colonna ci vanno gli n valori previsti yt, nella seconda gli n valori yt-SEprevym e nella terza i 60 valori yt+SEprevym. se stampiamo, sullo stesso piano cartesiano, xi,yi queste tre curve otteniamo la banda di confidenza per la previsione della media e così per l’altro caso.
Anche la funzione predict aiuta a plottare le bande.
La funzione simple.lm del Package UsingR di Venable plotterà ambedue le bande di confidenza, chiedendolo tramite il comando show.ci=T:
simple.lim(xi,yt, show.ci=T, conf.level=0.90)
USO DI PREDICT PER PLOTTARE LE BANDE DI CONFIDENZA
Per ottenere i valori predetti, si può usare in R la funzione predict che va chiamata attraverso un data.frame con dati x sulla colonna.
predict(resultreg, data.frame(x=c(50,60))) fornisce l’yt per queste due ascisse.
Per ogni x ordinato (x=sort(x)) però vogliamo 3 valori corrispondenti all’intevallo di confidenza:
predict(resultreg,data.frame(c=sort(x)) + level=0.9, interval=”confidence”) questo fa una tabella con tre colonne FIT LWR UPR: per plottare la banda inferiore usiamo la seconda colonna a cui si accede con [0,2] e con points.
plot(xi,yt)
abline(resultreg)
ci.lwr=predict(resulreg, data.frame(x=sort(x)), level=0.9, interval=”confidence”)[2]
Si aggiunge la banda con points
points(sort(xi), ci.lwr, typt=l”) # o si usa line()
Aternativamente, possiamo plottare l’altra con la funzione curve come segue:
curve(predict(resultreg, data.frame(x=x), interval=”confidence”)[,3], add=T)
Attenzione però perchè la funzione curve vuole una funzione di x non i dati! E’ difficile da interrompere.
Riassumendo proviamo queste linee in R:
Summary(resultreg)
predict(resultreg, data,frame(xi=sort(xi)), level=0.9, interval=”Confidence”)
c1.lwr= predict(resultreg, data.frame(xi=sort(xi)),level=0.9,intervall=”Confidence”)[,2]
points(sort(xi), ci.lwr, type=”l”),
ci.upr=predict(resultreg, data.frame(x=x), level=9.9, interval=”Confidence”, add=T)[,3]
points(sort(xi),ci.upr, type=”l”)
SCRIPTS DEL PROGRAMMA IN R RELATIVO ALLA REGRESSIONE LINEARE SEMPLICE: da confrontare gli outputs di R e quelli del Mathematica di Wolfram (programma scritto da P. Pistoia)!
library(graphics)
library(tseries)
library(UsingR)
library(lattice)
par(ask=T)
#Il seguente vettore dati è ottenuto togliendo dai 60 dati del
#vettore dati iniziale l’ESAs (effetto stagionale arsenico), ottenendo yt con #trend + random + ciclo
yt=c(0.0308,0.0460,0.0508,0.0643,0.0549,0.0604,0.0423,
0.0306,0.0502,0.0643, 0.0667,0.0555,0.0508,0.0430,
0.0658,0.0583,0.0750,0.0574,0.0693,0.0706,0.0602,
0.0443,0.0537,0.0605,0.0534,0.0610,0.0608,0.0683,
0.0580,0.0654,0.0708,0.0896,
0.0832,0.0713,0.0727,0.0815,0.0778,0.0795,0.0728,
0.0748,0.0590,0.0904,0.0723,0.0676, 0.0672,0.0823,
0.0707,0.0675,0.0838,0.0830,0.0728,
0.0723,0.0820,0.0614,0.0763,
0.0736,0.0742,0.0733,0.0637,0.0705)
par(ask=T)
options(digits=16)
ym=mean(yt)
ym
# LA REGRESSIONE con il calcolo di b0 e b1
xi=c(1:60)
n=length(xi)
n
plot(xi,yt, type=”l”)
abline(lm(yt~xi))
x=(xi-mean(xi))
y=(yt-mean(yt))
ai=x*y
Sxy=sum(ai)
Sx=sum(x)
Sy=sum(y)
xq=x^2
Sxq=sum(xq)
yq=y^2
qSx=Sx^2
b1=(n*Sxy+Sx*Sy)/(n*Sxq-qSx)
b0=sum(yt)/n-b1*sum(xi)/n
b1;b0
Yi=b0+b1*xi
resultreg=(lm(yt~xi)) # in resultreg ci vanno i risultati sulla yt originale
summary(resultreg) # trovo la maggior parte dei risultati
coef(summary(resultreg)) # trovo otto valori del risultato sotto forma di matrice
# 4 colonne: stima, SE, t-value, pr(>t)
b0=coef(summary(resultreg))[1,1]
b0
b1=coef(summary(resultreg))[2,1]
b1
SEb1=coef(summary(resultreg))[2,2]
SEb1
SEb0=coef(summary(resultreg))[1,2]
SEb0
#t0=b0/SEb0 # SEb0
#t1=b1/SEb1 # SEb1
n1=n-2
t=b1/SEb1
pt(t,n1,lower.tail=F)
#se l’ipotesi H0 è ß1=0.05 e Ha?0.05, calcoliamo a mano il p-value
ß1=0.05
t=(b1-ß1)/SEb1
pt(t,n1,lower.tail=F)
# Inferenza su b0
ß0=200
#SEb0=sqrt(Sq*sum(xi^2)/n*sum(xi-mean(xi))^2)
#standard error di b0
SEb0
t=b0/SEb0
t
pt(t,n1,lower.tail=F)
t=(b0-ß0)/SEb0 # se per ipotesi ß0=200:
t=(b0-ß0)/SEb0
pt(t,n1,lower.tail=T) # la coda più bassa (<200)
res=resid(resultreg)
summary(res)
plot(resultreg) #aspetta per confermare cambio pagina…
par(mfrow=c(2,2))
plot(resultreg)
Sq=sum(res^2)/(length(xi)-2) # stima di sigma^2
S=sqrt(Sq) #deviazione stardard dei residui
S
CONTI CHE TORNANO
# inferenze su b1
delta2=(xi-mean(xi))^2
Sx2=sum(delta2)
SEb1=S/sqrt(Sx2)
SEb1
SEb1=S/sqrt(sum((xi-mean(xi))^2))
SEb1
t=b1/SEb1 # statistica campionaria di b1
t
# Si trova il valore p rispetto alla distribuzione t, se ß1=0
n1=length(xi)-2
pt(t,n1,lower.tail=F)
#se l’ipotesi H0 è ß1=0.05 e Ha?0.05, calcoliamo a mano il p-value
ß1=0.05
t=(b1-ß1)/SEb1
pt(t,n1,lower.tail=F)
# Inferenza su b0
ß0=200
SEb0=S*sqrt(1/n+(mean(xi))^2/Sx2)
#standard error di b0
SEb0
t=b0/SEb0
t=b0/SEb0
t
t=(b0-ß0)/SEb0 # se per ipotesi ß0=200:
t=(b0-ß0)/SEb0
pt(t,n1,lower.tail=T) # la coda più bassa (<200)
#CALCOLO DI R-QUADRO E TEST F DI FISCHER per R-quadro_pop=0#
# Calcolo Total Sum of Square (TSS)#
TSS=sum((yt-mean(yt))^2)
TSS
# Calcolo Regression Sum of Square (REGSS)#
REGSS=sum((Yi-mean(yt))^2)
REGSS
# Calcolo Residual Sum of Square(RESSS)#
RESSS=sum(res^2)
RESSS
# La differenza TSS-(REGSS+RESSS) deve essere 0#
TSS-RESSS-REGSS
# Calcolo Mean Square Regression (MSREG)#
p=1
MSREG=REGSS/p
MSREG
# Calcolo Mean Square Residual (MSRES)#
MSRES=RESSS/(n-p-1)
MSRES
# Calcolo Total Mean Square (TMS)
TMS=TSS/(n-1)
TMS
# Calcolo l’R-quadro che è il coefficiente di correlazione
# fra xi e yt, oppure fra yr e yt, ovvero rappresenta
# la percentuale di variazione degli yt spiegata dalla
# regressione.
Rq=REGSS/TSS
Rq
# Calcolo l’R-quadro aggiustato per la popolazione
Rqagg=1-Sq/TMS
Rqagg
# Calcolo la statistica F di Fischer
F=MSREG/MSRES
F
# Calcolo la probabilità corrispondente alla # # ascissa F. Se tale probabilità è > di 0.975#
# (livello di significanza 0.025 a due code) #
# si respinge l’ipotesi nulla.#
pf(F,p,n-p-1,lower.tail=T)
# BANDE DI CONFIDENZA
par(mfrow=c(1,1))
yt=yt*100 # ricordiamoci di pensare divise per 100 le ordinate del grafico.
# poiche la pendenza non è risolvibile nel grafico, si fa dinuovo la regressione con yt*100
resultreg=(lm(yt~xi))
summary(resultreg)# da i risultati per i punti (xi,yt*100) confrontare con quelli (xi,yt)!
plot(xi,yt) #fa uno scatterplot dei dati e vi aggiunge la retta di regressione
abline(resultreg) #si costruisce la base per aggiungere le bande.
predict(resultreg, data.frame(xi=sort(xi)), level=0.9, interval=”confidence”)
ci.lwr= predict(resultreg, data.frame(xi=sort(xi)),level=0.9,interval=”confidence”)[,2]
points(sort(xi), ci.lwr, type=”l”)
ci.upr=predict(resultreg, data.frame(xi=xi), level=.9, interval=”confidence”, add=T)[,3]
points(sort(xi),ci.upr, type=”l”)
#Usiamo un comando di più alto livello del package UsingR di Venable
resultreg=simple.lm(xi,yt)
summary(resultreg)
simple.lm(xi,yt,show.ci=T,conf.level=0.95,pred=)
COME SI FA A VEDERE SE QUESTO MODELLO E’ ACCETTABILE CON IL MATHEMATICA DI WOLFRAN. Scripts di Piero Pistoia
Applichiamo il modello di regressione semplice, come esempio, su tre possibili vettori dati di serie storiche mutuati da una mia ricerca su dati reali relativi a 60 concentrazioni mensili (5 anni) di arsenico nelle acque potabili delle Sorgenti Onore della Carlina (montagna a cavallo di tre provincie, Siena, Firenze, Pisa) che integra l’acquedotto dell’Alta val di Cecina (Pi). Nei remarks iniziali è riportata in breve come sono stati costruiti questi vettori all’interno della ricerca stessa, accennando anche ai processi serviti per il loro calcolo. I vettori verranno inseriti uno alla volta eliminando le virgolette agli estremi; vengono allegati alcuni grafici costruiti dal programma. La ricerca verrà a suo tempo inserita nel blog, come esempio di analisi statistica su dati reali. Con qualche variazione sui valori dell’asse x è possibile inserire coppie di vettori x,y qualsiasi rendendo questo uno strumento efficace per testare ogni retta in ogni piano cartesiano. Brevi remarks sono stati abbinati anche agli svariati tests statistici condotti. Le diverse linee di programma dovranno essere riscritte sulla console del Mathematica (vers.4.x o anche la vers. 2.x ), con molta attenzione. Buon divertimento per quelli che lo vorranno fare.
SCRIPTS DI P. PISTOIA RELATIVO ALLA REGRESSIONE SEMPLICE CON IL LINGUAGGIO DEL MATHEMATICA DI WOLFRAM
“Si hanno dati mensili, per 5 anni (60 dati), di concentrazioni As delle
sorgenti Onore della Carlina, che servono l’Alta val di Cecina; così avremo 5
concentrazioni per i 5 gennaio, 5 concentrazioni per i 5 frebbraio e così
via. Si mediano poi per ogni mese questi 5 valori per ottenere le 12 medie
seguenti a partire da gennaio.
E’ interessante notare come abbiamo ottenuto un’oscillazione in 12 mesi fattori stagionali, che potremmo estendere ai 5 anni con il comando rep, ottenendo l’effetto stagionale (ancora 60 dati) che toglieremo dai dati originali yt, al fine di avere yt1 (ciclo+trend+random). Per vedere ‘cosa c’è dentro’ gli si
applica il periodogramma.”
“yt={0.307,0.301,0.324,0.312,0.363,0.348,0.385,0.359,0.314,0.294,0.309,0.299}”
“yt=yt/5”
“I 48 dati seguenti sono stati ottenuti da 60 dati mensile, sempre dell’As,
togliendo da essi il vettore dati ottenuto da una media mobile di ordine 12 eseguita sugli stessi. In tal modo si viene a togliere dai dati originali l’oscillazione di ordine dodici (vettore asf12), scoperta con un periodogramma applicato ad essi. Allora questi 48 dati, dopo la sottrazione di asf12, conterranno ancora trend e ciclo (datitc), se l’operazoione di media avrà
eliminato i random. Su essi potremo appliare un processo che porta all’individuazione di una retta di regressione”
“>yt={0.0483,0.0527,0.0533,0.0537,0.0543,0.0550,
0.0560,0.0588,0.0609,0.0605,0.0591,0.0588,0.0591,0.0598,0.0603,0.0605,0.0602,0.0598,
0.0602,0.0611,0.0628,0.0649,0.0668,0.0685,0.0704,0.0721,0.0734,
0.0742,0.0745,0.0756,0.0767,0.0758,0.0743,0.0740,0.0744,0.0738,0.0734,0.0738,
0.0740,0.0739,0.0747,0.0745,0.0734,0.0738,0.0744,0.0743,0.0736,0.0735}”
“Il vettore asf12 (48 dati) viene utilizzato per l’elaborazione dei 12 fattori stagionali, detti AsFS, (prendendo tutti i valori di gennaio diviso 4 (media dei 4 gennaio), tutti valori di febbraio diviso 4 (media dei 4 febbraio) fino al dodicesimo fattore per dicembre. Si costruisce poi il vettore effetto stagionale (AsES) di 60 dati allineando a partire dal gennaio iniziale, questi dodici fattori stagionali ripetuti 5 volte, coprendo 60 dati. I 60 dati seguenti si ricavano sottraendo dal vettore yt (60 dati) iniziale il vettore di 60 dati dell’effetto stagionale; in tal modo si libera da yt l’effetto stagionale (AsES).In y1t che rimane ci dovrebbero essere ciclo, trend e random, Su di esso proveremo una regressione lineare semplice”
yt={0.0308,0.0460,0.0508,0.0643,0.0549,0.0604,0.0423,0.0306,0.0502,0.0643, 0.0667,0.0555,0.0508,0.0430,0.0658,0.0583,0.0750,0.0574,0.0693,0.0706,0.0602,
0.0443,0.0537,0.0605,0.0534,0.0610,0.0608,0.0683,0.0580,0.0654,0.0708,0.0896,
0.0832,0.0713,0.0727,0.0815,0.0778,0.0795,0.0728,0.0748,0.0590,0.0904,0.0723,0.067, 0.0672,0.0823,0.0707,0.0675,0.0838,0.0830,0.0728,0.0723,0.0820,0.0614,0.0763,
0.0736,0.0742,0.0733,0.0637,0.0705}

p1 = ListPlot[yt, PlotJoined -> True,
PlotRange -> Automatic, GridLines -> {Automatic, Automatic}]
x9 = N[Table[i, {i, 1, Length[yt]}]];
c1 = x9;
For [i = 1, i < Length[yt] + 1, i++, j = i*2; c = c1; yi = yt[[i]];
c = Insert[c, yi, j]; c1 = c];
d = Partition[c, 2]
c
f[x_] := Fit[d, {1, x}, x]
z1 = Transpose[d][[1]];
z2 = Transpose[d][[2]];
yi = z2;
x1 = Min[z1];
x2 = Max[z1];
n = Length[z1]
B0 = f[x] /. x -> 0
f[0]
f1 = f[x] /. x -> 1
f[1]
B1 = f1 – B0
m[list_List] := Apply[Plus, list]/n
xv[list_List] := m[(list – xmedia)^2]
xmedia = m[z1]
ymedia = m[z2]
xvar = xv[z1]
<< Statistics`DescriptiveStatistics`
<< Statistics`ContinuousDistributions`
<< Graphics`Legend`
xmedia = Mean[z1]
xvar = Variance[z1]
yvar = Variance[z2]
yr = f[x] /. x -> z1;
RES = yi – yr;
sd = RES^2;
“Calcolo Total Sum of Square (TSS)”
TSS = Apply[Plus, (yi – ymedia)^2]
“———————————–”
“Calcolo Regression Sum of Square (REGSS)”
REGSS = Apply[Plus, (yr – ymedia)^2]
“———————————–”
“Calcolo Residual Sum Of Square (RESSS)”
RESSS = Apply[Plus, sd]
“———————————–”
“Calcolo Mean Square Regression (MSREG)”
p = 1
MSREG = REGSS/p
“———————————–”
“Calcolo Mean Square Residual (MSRES)”
MSRES = RESSS/(n – p – 1)
“———————————–”
“Calcolo Total Mean Square (TMS)”
TMS = TSS/(n – 1)
“———————————–”
“Calcolo R-quadro che è il coefficiente di”
“correlazione fra x e y, oppure fra yi e yr,”
“ovvero rappresenta la percentuale di”
“variazione degli yi spiegata dalla”
“regressione”
Rq = REGSS/TSS
“———————————–”
“Calcolo l’R quadro aggiustato per stimare il”
“corrispondente parametro della popolazione”
ESS1 = Apply[Plus, sd];
ESS2 = ESS1/(n – 2);
TSS2 = TSS/(n – 1);
Rqagg = 1 – ESS2/TSS2
“———————————-”
“Calcolo la Statistica F (MSREG/MSRES)”
” che ha la distribuzione di Fisher”
F = MSREG/MSRES
“———————————–”
“Calcolo i livelli di significanza al 95%”
“(2 code) della F di Fisher. Se la F è >”
“(coda a destra) di F95% siamo autorizzati”
“a respingere l’ipotesi nulla (Rq=0 nella”
“popolazione”
ndist = FRatioDistribution[p, n – p – 1]
F95 = Quantile[ndist, (0.95 + 1)/2] // N
“———————————–”
“Calcolo anche la probabilità (Area)”
“corrispondente all’ascissa F. Se risulta”
” > di 0.975 cade nella zona proibita”
CDF[ndist, F] // N
“———————————–”
“Calcolo l’Errore Standard della Stima o”
“Deviazione Standard dei Residui. Si tratta della”
“stima della Deviazione Standard delle distribuzioni”
“della variabile dipendente per ogni xi”
ESS = Sqrt[ESS1/(n – 2)] // N
“———————————–”
“Calcolo t-critico all’inizio della coda corrispondente”
“ad un’area di 0.975 in una distribuzione di Student a”
“n-1 gradi i libertà e ad n-2”
ndist1 = StudentTDistribution[n – 1]
ndist2 = StudentTDistribution[n – 2]
t1 = Quantile[ndist1, {0.95 + 1}/2] // N
t2 = Quantile[ndist2, {0.95 + 1}/2] // N
“———————————–”
“Calcolo l’Errore Standard di B0 (SB0) e di B1 (SB1).”
” Ricavo poi il valore campionario di tB0 (B0/SB0)”
” e tB1 (B1/SB1), per controllare se B0 e B1 nella”
” popolazione hanno valore zero”
SB0 = ESS Sqrt[1/n + xmedia^2/((n – 1) xvar)]
SB1 = ESS/Sqrt[(n – 1) xvar]
tB0 = B0/SB0
tB1 = B1/SB1
“———————————–”
“Calcolo A: area (probabilità) lasciata a sinistra”
” dell’ascissa tB0 nella sua distribuzione, una ”
“Student a n-2 GL. P=1-A è la probabilità lasciata”
” a destra di tB0 (Livello di Significanza); se ”
“questa è < di 0.025 si respinge l’ipotesi nulla”
” (B0 e/o B1 nulli nella popolazione) ”
A = CDF[ndist2, tB0]
P = 1 – A
“———————————–”
“Faccio un calcolo analogo per B1”
A1 = CDF[ndist2, tB1]
P1 = 1 – A1
“———————————–”
“Calcolo ora gli Intervalli di Confidenza al 95% di”
” B0 e B1, nei quali con la probabilità del 95% ”
“cadranno i rispettivi valori della popolazione”
B0 + t2 SB0
B0 – t2 SB0
B1 + t2 SB1
B1 – t2 SB1
“———————————–”
“Calcolo l’Errore Standard della Stima funzione”
“di (x-xmedia) nel caso di pochi dati”
k[x_] := t1 ESS Sqrt[((n + 1)/n + (x – xmedia)^2/((n – 1) xvar))]
“———————————–”
ymin = Floor[f[Floor[x1]] – k[Floor[x1]]]
ymax = Ceiling[f[Ceiling[x2]] + k[Ceiling[x2]]]
Plot[{f[x], f[x] + k[x], f[x] – k[x]},
{x, Floor[x1], Ceiling[x2]},
PlotStyle ->
{{AbsoluteThickness[0.001]},
{AbsoluteThickness[0.001], AbsoluteDashing[{5, 5}]},
{AbsoluteThickness[0.001], AbsoluteDashing[{5, 5}]}},
PlotLabel -> FontForm[Rqagg “->Rq-Aggiustato”, {“Times”, 12}],
PlotLegend -> {“Curva Regressione”, “Limite Interv Conf 95 %”,
“Limite Interv Conf 95 %”},
LegendPosition -> {0.8, 0},
AxesOrigin -> {Automatic, Automatic},
AxesLabel -> {“Igrometro di prova”, “Igrom. di riferimento”},
GridLines -> {Automatic, Automatic},
Evaluate[Epilog -> {PointSize[0.01], Map[Point, d]}]]

“ANALISI DEI RESIDUI”
“Con i residui è possibile controllare se le assunzioni”
“di linearità, normalità e varianza costante, richieste”
“per l’analisi della regressione lineare, sono o no soddisfatte.”
“Basta costruire il grafico dei Residui Standardizzati sulle”
” ordinate e la variabile indipendente standardizzata sulle”
” ascisse e/o quello dei Residui Studentizzati con ancora”
“la variabile indipendente standardizzata sulle ascisse”
VIS = (z1 – xmedia)/Sqrt[xvar];
RESSTA = RES/ESS;
k1 = Flatten[k[x] /. x -> z1];
n0 = Length[k1];
RESSTU = RES/k1;
n1 = Length[VIS];
n2 = Length[RESSTA];
n3 = Length[RESSTU];
c1 = VIS;
c = VIS;
w = n + 1
For[i = 1, i < w, i++,
j = i*2; c = VIS; yi = RESSTA[[i]];
c = Insert[c, yi, j]; VIS = c]
d1 = Partition[c, 2];
Length[d1];
ListPlot[d1]
For[i = 1, i < w, i++,
j = i*2; c = c1; yi = RESSTU[[i]];
c = Insert[c, yi, j]; c1 = c]
d2 = Partition[c, 2];
Length[d2];
ListPlot[d2]

ALGEBRA MATRICIALE PER REGRESSIONI ANCHE MULTILINEARI E MATRICE INVERSA; CON ESEMPI DI CALCOLO (dal blog cercare “Un parziale percorso di base…, dello stesso autore)
COME ‘FITTARE’ UNA COMBINAZIONE DI ONDE DEL SENO AI DATI DI UNA SERIE STORICA (dal blog cercare “Un parziale percorso di base…”)
SCRIPTS del PERIODOGRAMMA prima parte
#In ogni caso gli scripts dei programmi presentati in R possono essere trasferiti #direttamente sulla console di R con Copia-Incolla: il programma inizierà #nell’immediato a girare costruendo risultati e grafici i cui significati sono riassunti #nei remarks.
# INIZIO ANALISI DI FOURIER IN FORMA DI FUNCTION (a cura di P. Pistoia).
t=c(1:21)
yt=100+4*sin(2*t/21*2*pi-pi/2)+3*sin(4*t/21*2*pi+0)+
6*sin(5*t/21*2*pi-1.745)
m =(n-1)/2 # perchè n dispari
PRDGRAM<- function(yt,m) {
#alfa=-pi/2 -> 270°; alfa=-1.175 rad (cioè -100°) -> 260°
n=length(yt)
t=c(1:n)
yt=as.vector(yt)
#m =(n/2-1) # perchè n pari
#m= numero amoniche da cercare nei dati
# libray(tseries)
# VALORI DEL PARAMETRO ak
a0=c(); k=0; a0=0;
for(t in 1:n){a0=a0+yt[t]*cos(2*pi*t*k/n)}
a0
a0=a0*2/n;a0=a0/2
a0
a=c();a[1:m]=0;
for(k in 1:m) {
for(t in 1:n){
a[k]=a[k]+yt[t]*cos(2*pi*t*k/n)}}
a=2*a/n
# vALORI DEL PARAMETRO bk
b=c();b[1:m]=0;b0=0;k=0
for(k in 1:m) {
for(t in 1:n){
b[k]=b[k]+yt[t]*sin(2*pi*t*k/n)}}
a <- as.vector(a)
for(i in 1:m){
if (abs(a[i]) < 1e-10) a[i]=0 else a[i]=a[i]}
a
for(i in 1:m){
if (abs(b[i]) < 1e-10) b[i]=0 else b[i]=b[i]}
b=2*b/n
b
# aMPIEZZE
ro <- sqrt(a^2 +b^2)
ro
for(i in 1:m){
if (abs(ro[i]) < 1e-10) ro[i]=0 else ro[i]=ro[i]}
ro
# CALCOLO DELLA FASE DI OGNI ARMONICA
# RIPORTANDO IL VALORE AL QUADRANTE GIUSTO
for(i in 1:m){
f2[i] <- abs(a[i]/b[i])
f2[i] <- atan(f2[i])*180/pi}
f2 =as.vector(f2)
f2
phi <- c()
for(i in 1:m){
# f2 <- abs(a[i]/b[i]);
# f2 <- atan(f2)*180/pi;
if(b[i]>0 & a[i]>0) phi[i] = f2[i];
if(b[i]<0 & a[i]>0) phi[i] = 180-f2[i];
if(b[i]<0 & a[i]<0) phi[i] = 180+f2[i];
if(b[i]>0 & a[i]<0) phi[i] = 360-f2[i];
if(b[i]==0 & a[i]==0) phi[i] = 0;
if((b[i]<0 & a[i]>0) | a[i]==0) phi[i]=0;
if(b[i]==0 & a[i]>0) phi[i]=90;
if(b[i]==0 & a[i]<0) phi[i]=360-90
}
# PHI FASE ARMONICHE
phi=as.vector(phi)
phi
param_a <-a
param_b <-b
ampiezza <- ro
fase <- phi
data <-data.frame(param_a,param_b,ampiezza, fase)
data
par(mfrow=c(1,4))
plot(a, xlab=”Armoniche = N° osclllazioni in 21 dati”)
plot(b, xlab=”Armoniche = N° osclllazioni in 21 dati”)
r0=as.vector(ro)
plot(ro,type=”l”,main=”PERIODOGRAMMA di dati”,
xlab=”Armoniche = N° osclllazioni in 21 dati”, ylab=”ampiezza”)
# for(i in 1:10000000) i=i
# lines(phi,type=”l”)
plot(phi,type=”l”,main=”PERIODOGRAMMA di dati”,
xlab=”Armoniche = N° osclllazioni in 21 dati”, ylab=”Fase”)
}
FINE SUBROUTINE ANALISI FOURIER
Richiamo function
PRDGRAM(yt,m) # gira la function del periodogramma di yt ed esce il seguente grafico:

SCRIPTS del PERIODOGRAMMA seconda parte
#ESERCITAZIONI COL PROGRAMMA SCRITTO IN R vers. del 16-07-19011
#Nel precedente intervento simulavamo ad hoc una serie storica
#’tabellando’ 21 dati da tre funzioni del seno con costante additiva 100,
#con ampiezze rispettivamente 4,3,6 e ‘frequenze’ nell’ordine 2/21, 4/21,
#5/21 e infine fasi -pi/2, 0, -1.745.
#Abbiamo cioè calcolati in yt 21 dati attribuendo a t valori da 1 a 21
#nell’espressione scritta nel precedente listato. Tali dati rappresentavano
#proprio la nostra serie storica da sottoporre al Periodogramma. Tramite
#il nostro programma in R calcolammo allora i valori di ampiezze e fasi
#per le prime 10 armoniche riscoprendo nei dati le oscillazioni che c’erano.
#Per esercizio continuiamo a simulare serie storiche con espressioni
#di base analoghe modificandole, aggiungendo anche un trend lineare (x*t) e
#valori random onde controllare se il Periodogramma riesce a”sentire”,
#oltre alle oscillazioni armoniche, anche il trend e la componente casuale.
#Con l’istruzione ‘#’ elimineremo secondo la necessità le linee di
#programma non utilizzate per lo scopo prefissato.
#In ogni caso gli scripts dei programmi presentati possono essere trasferiti #direttamente sulla console di R con Copia-Incolla: il programma inizierà #nell’immediato a girare costruendo risultati e grafici i cui significati sono riassunti #nei remarks.
#Proveremo ad applicare il programma su 21 dati simulati dalle
#espressioni di una retta inclinata e da una serie random estratta da
#una distribuzione gaussiana. Intanto però sceglieremo una combinazione di seni
#interessanti più adatta a proseguire l’esercitazione.
#n=21
t=c(1:n)
#yt=0.5*t
# si tratta di una iperbole
#yt=c();yt[1:t]=0
#yt <- rnorm(t,0,1)
#yt=-4+ 0.5*t + rnorm(t,0,1)
#t=c(1:21)
#yt=100+4*sin(2*t/256*2*pi-pi/2)+3*sin(4*t/256*2*pi+0)+
#6*sin(5*t/256*2*pi-1.745) #analisi yt; tenendo come base questa espressione
# con armoniche basse, ro è sulla rampa alta dell’iperbole.
#yt=100+4*sin(2*t/n*2*pi-pi/2)+3*sin(4*t/n*2*pi+0)+
#6*sin(5*t/n*2*pi-1.745) + 0.1*t # analisi ytreg
#yt=100+2*sin(2*t/n*2*pi-pi/2)+sin(4*t/n*2*pi+0)+
#3*sin(5*t/n*2*pi-1.745) + rnorm(t,0,1)*2 # analisi ytrnorm: diminuiamo le
#ampiezze e aumentiamo i random
#yt=100+4*sin(2*t/n*2*pi-pi/2)+3*sin(4*t/n*2*pi+0)+
#6*sin(5*t/n*2*pi-1.745) + 0.5*t)+(rnorm(t,0,1)-1/2)) # analisi ytregrnorm
n=240
t=c(1:n);
yt <- 4*sin(5*t/n*2*pi)+2*sin(2*pi*30*t/n)+ 3*sin(40/n*t*2*pi)+0.1*t +
rnorm(n,0,1)*2
# questa espressione con ‘frequenze’ alte (30,40) è
#più indicata a dimostrare che il Periodogramma ‘scopre’ anche trends
#e random oltre alle oscillazioni sinusoidali.
#Ora possiamo prevedere che cosa accade se togliamo una o due di queste tre #oscillazioni,
#basta far girare il programma nei diversi casi.
#In questo contesto al termine useremo invece, per esercizio, le
#tecniche di scomposizione di una serie storica:
#proviamo a ‘destagionalizzarla’ con due o tre medie mobili
#opportune (o magari col comando filter di R) per controllare che cosa
#rimane sottraendo da yt l’oscillazione relativa alla media mobile usata (che cosa accade ai random?). Potevamo anche’detrendizzarla’ prima
#con una regressione lineare, ovvero eliminare i random con una media
#mobile 3*3 ecc..
#m =(n-1)/2 # perchè n dispari
yt=as.vector(yt)
#m =(n/2-1) # perchè n pari
#Sarebbe possibile anche ‘meccanizzare’ il precedente processo.
m=50 # numero armoniche da cercare nei dati scelte manualmente
library(tseries)
PRDGRAM(yt,m) #RICHIAMO DELLA FUNCTION e gira il periodogramma per i nuovi dati posti in yt::

Le linee successive sono in attesa di correzione-eliminazione se la function funziona!
#CENNI: ‘DESTAGIONALIZZAZIONE’ DEI DATI CON ‘FILTER’ E CON MEDIE MOBILI (da correggere e precisare: AD MAIORA!)
filt12 <- filter(yt,filter=rep(1/13,13))
filt12 <- as.vector(filt12);length(filt12)
x=seq(1:240)
fit12 <- lm(filt12~x)
summary(fit12)
b0=fit12$coefficients[1]
b1=fit12$coefficients[2]
y=b0+b1*x
ts.plot(filt12)
abline(fit12)
length(filt12);length(y)
for(i in 1:10000000) i=i
filt12=filt12[7:234]
y=y[7:234]
detrend <- filt12-y
acf(detrend)
for(i in 1:10000000) i=i
ts.plot(detrend)
for(i in 1:10000000) i=i
#par(mfrow=c(1,4)) # cancelliamo ‘#’ davanti a par per vedere i grafici insieme
ts.plot(yt); for(i in 1:10000000) i
filt12 <- filter(yt,filter=rep(1/13,13))
ts.plot(filt12);for(i in 1:10000000) i
filt72 <- filter(yt,filter=rep(1/73,73))
ts.plot(filt72);for(i in 1:10000000) i
filt96 <- filter(filt96,filter=rep(1/97,97))
ts.plot(filt96);for(i in 1:10000000) i
#E’ interessante notare con tre medie mobili centrate (non pesate!) di ordine #rispettivamente 12,72,96 in successione o come vi pare, possiamo eliminare da yt #(con yt-filtn) i tre picchi (5, 30, 40) del periodogramma ‘applicato’ alla seguente #espressione trigonometrica che simulava i dati:
# yt <- 6*sin(5*t/n*2*pi) + 2*sin(2*pi*30*t/n) +
# 3*sin(40/n*t*2*pi) + 0.1*t + rnorm(n,0,1)*2,
# lasciando un’iperbole ‘pulita’ a rappresentare (da controllare!)
# la retta di regressione. Da ricordare come con le medie mobili
# si eliminano anche i valori casuali.
# Che cosa accade dei picchi se cambio n?
#n=100 #n° armoniche rilevanti rimarranno ancora a freq. 5, 30 40!
#Come esercizio ‘inventiamo’ una routine che calcoli una media mobile
#di ordine k (es.,k=12)
k=12
k=k/2+1 #se pari
k= k=(k-1)/2 #se k=pari
yt=as.vector(yt) #yt è il vettore su cui si applica la media mobile
ly=length(yt)
filt=c()
for(t in 7:ly){filt[t]=
(yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+yt[t-1]+yt[t]+
yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+yt[t+6]/2)/13}
filt #Si confrontino i valori delle medie mobili calcolate con
filt12 #la definizione di media mobile e con il comando filter:
# E’ da notare che le due serie di valori differiscono perché la
# prima serie è ottenuta da una media mobile centrata e pesata.
# Eliminando la divisione per 2 dei termini estremi avremo lo
# stesso risultato (controllare).
Dott. Piero Pistoia
 ______________________________________________________
______________________________________________________

































