ATOMO DI IDROGENO E MODELLO DI BOHR; del dott. prof. Giorgio Cellai

Atomo di idrogeno e modello di Bohr 1

MECCANICA RELATIVISTICA del dott. prof. Giorgio Cellai

Post in via di costruzione…

Per vedere  gli articoli del prof. Cellai in successione, cliccare sotto:

Cinematica rel. 1,2. pdf

—————————

Tre applicazioni del concetto di tempo proprio dell’articolo precedente:

rel. 2.2-cinematica-prof. Cellai.pdf

—————————————-

Cenni di dinamica relativistica-Il sillabario

—————————————————–

 

SCALA MUSICALE “UNIVERSALE”; dott. prof. Giorgio Cellai

Il seguente articolo rappresenta il quarto articolo dopo Induzione Matematica, Successioni sui numeri reali, Progressioni sui reali, costituenti nell’insieme un modulo di insegnamento. Si può leggere in successione  l’intero modulo in questo blog cercando BREVI LEZIONI

Per leggere questo scritto in pdf, cliccare su:

Articolo scala temperata1

BREVI LEZIONI : “PRINCIPIO DI INDUZIONE MATEMATICA”; “SUCCESSIONI E NUMERI REALI”; “PROGRESSIONI E NUMERI REALI”; “SCALA MUSICALE UNIVERSALE “; del dott. prof. Giorgio Cellai

Post in via di costruzione…

Per leggere le prime tre lezioni del modulo di Cellai in pdf cliccare sotto:

cellai_modulolezioni_induzione_successioni_progressioni0001

Per leggere la quarta lezione del modulo di Cellai “Scala Musicale temperata” di Cellai in pdf  cliccare sotto:

Articolo scala temperata1

 

Testo della lezione “INDUZIONE MATEMATICA” in  jpg:

INDUZIONE MATEMATICA

 

Dott. prof. Giorgio Cellai

Da notare che Cellai ci informa che questa breve lezione si trova inserita in un modulo didattico da lui proposto sulle “Successioni matematiche ed altro” e presto lo vedremo qui pubblicato.

Si può leggere, più chiaramente, l’articolo di Cellai anche in pdf, cliccando sul link seguente:

PRINCIP_INDUZ0001

 

Testo della lezione “SUCCESSIONE E NUMERI REALI” in pdf:

SUCCESSIONI E NUMERI REALI

Possiamo leggere la lezione “Successioni e numeri reali”  in pdf cliccando sul link sotto:

successioni-e-numeri-reali12-1

Testo della lezione “PROGRESSIONI E NUMERI REALI” in pdf:

PROGRESSIONI E NUMERI REALI

Possiamo leggere la lezione “Progressioni e numeri reali” in pdf cliccando sul link sotto:

PROGRESSIONI E NUMERI REALI0001

LA CADUTA DEI GRAVI A PIU’ DI QUATTRO SECOLI DA GALILEO; analisi e significati di alcune sottigliezze nell’insegnamento della fisica e laboratorio al biennio superiore: un metodo di insegnamento; del dott. prof. Piero Pistoia et al.

CURRICULUM DI PIERO PISTOIA :

 

piero-pistoia-curriculumok-1-19Download

Da rivedere…

LA CADUTA DEI GRAVI A PIU’ DI QUATTRO SECOLI DA GALILEO

Significati, analisi e sottigliezze, con un certo rischio, su alcuni aspetti dell’insegnamento della fisica e laboratorio, al Biennio Superiore; a cura di Piero Pistoia et al.

INTRODUZIONE

Riteniamo giustificato, secondo criteri epistemologici (1), psicologici (2) e didattici (3), un metodo di insegnamento della Fisica, non di tipo induttivista, ma caratterizzato, in generale, da particolari processi ipotetico-deduttivi. E’ da dire, per la verità, che, mentre per la filosofia e la logica tale metodo è falso e quindi da abbandonare, di fatto non lo è sempre per la stessa Scienza operativa e per il senso comune. Nonostante le critiche alla epistemologia popperiana (vedere i post relativi su questo blog) questa filosofia, secondo lo scrivente ed altri, è degna di rispetto perché degnamente si accorda con un insegnamento formativo nella scuola!

Consideriamo altresì che il così detto metodo sperimentale di Galileo, alla luce anche delle ultime interpretazioni del suo pensiero (4), abbia in effetti analoghe caratteristiche.

Secondo tale metodo l’insegnamento deve partire da problemi (nell’accezione data alla parola da Popper, Antiseri et al.), per arrivare, attraverso le teorie tentative di soluzione (TT di Popper), al processo sperimentale di controllo (corroborazione, falsificazione), fino al nuovo problema, fasi che devono razionalmente e consapevolmente esplicitate nel corso di un insegnamento formativo, come è un Biennio Superiore.

Diversi sono i problemi che devono essere affrontati in successione per ‘costruire’ in una classe di un Biennio, la disciplina, sotto la guida dell’insegnante, ‘alcuni’ dei quali, importanti ed obbligati in quanto innescano a cascata una sequenza di altri, sono qui di seguito sinteticamente nominati:

a – Nella caduta dei gravi con attrito trascurabile e al tempo-iniziale, t₀=0 s e v-iniziale, V₀= 0 m/s (condizioni al contorno), che relazione ci sarà fra velocità di caduta istantanea e tempo e fra velocità istantanea e spazio percorso?

b – Che relazione ci sarà fra modulo della forza applicata ad un oggetto, che si muova con attrito trascurabile su un piano orizzontale e il modulo dell’accelerazione acquistata (vettore forza e vettore accelerazione con stessa direzione e stesso verso)?

c – Che relazione ci sarà fra quantità di carica elettrica posta su un conduttore isolato (o su un’armatura di un condensatore e l’altra messa a terra) ed il potenziale da esso assunto? (5))

d – Che relazione ci sarà fra (Va-Vb) misurata ai capi di un resistore e la Ic misurata in una sezione di esso?

e – Che relazione ci sarà fra il flusso di induzione magnetica concatenato ad un circuito e l’intensità di corrente in esso circolante?

Ognuno di questi problemi e degli altri della stessa forma matematica non nominati deve essere discusso in classe fino a formulare una o più ipotesi plausibili (non necessariamente ‘vere’), per poi progettare un esperimento di controllo. Nella zona di ‘corroborazione’ o di ‘falsificazione’ dell’ipotesi nascerà il nuovo problema e, se l’ipotesi verrà corroborata (avvalorando magari il risultato facendo riferimenti ad analoghi esperimenti condotti in laboratori di ricerca), avremo ‘costruito in classe un ‘pezzetto’ di fisica!

In questo l’autore cercherà di analizzare il problema a, precisandone aspetti e implicazioni educative e formative, riscoprendo nella caratteristica dialogica di tipo galileiano di condurre il discorso e nei precisi e puntuali interventi di Salviati nei confronti di Simplicio, la chiave per ricostruire la fisica anche nelle classi di oggi.

ANALISI E DISCUSSIONE DEL PROBLEMA RELATIVO ALLA CADUTA DEI GRAVI

problema (a) e formulazione delle ipotesi

Focalizziamo l’attenzione e la memoria degli alunni sulla caduta di oggetti pesanti, sui quali le azioni di disturbo dell’aria sono meno evidenti, almeno per basse velocità.

Alla domanda su come si comporterà la velocità durante il movimento, si hanno in generale perplessità. I nostri ragazzi di 14-15 anni hanno o dovrebbero avere la mente del Simplicio galileiano. Alcuni conoscono già le risposte a memoria, secondo noi, purtroppo, fornite probabilmente su informazioni parziali, disperse, prima che si formulassero le ipotesi, prima che si precisassero le aspettative, prima delle delusioni dinanzi ad ipotesi sbagliate, prima insomma dei processi che innescano il vero apprendimento! E’ un po’ come insegnare direttamente le formule da imparare a mente, per poter fare da subito con esse i così detti esercizi di applicazione di esse, riportati sul libro di testo!

Qualche frammento di ricordo culturale precedente scarsamente assimilato, certi mass media, certi personal media, qualche software selvaggio e poco calibrato, avranno fornito queste nozioni fine a se stesse.

IL maggiore tradimento, pur inconsapevole, che la civiltà tecnologica abbia mai perpetrato ai danni dei cuccioli della specie secondo lo scrivente è proprio questo: sono stati gettati in un contesto tecnologico di natura altamente simbolica e lontano così dalla teorie del senso comune, pur coronato eccezionalmente da buon senso, ‘il buon senso del senso comune’, a cui gli alunni possono essere vicini, in un mondo incomprensibile, nel quale i messaggi si trasformano in nozioni isolate senza contesto da memorizzare e delle quali sfuggono le ragioni più profonde, in un mondo dove i ‘messaggi’ svuotati dal ‘mezzo’, per mutuare le parole di McLuan, annebbiano curiosità e meraviglia, uniche molle del progresso umano.

Fortunati se c’è ancora qualche Simplicio, che vede cadere dalla mano il grave subito velocemente appena lasciato. Allora, a guisa del Salviati galileiano l’insegnante può guidare la discussione, al di là di tutto, del tempo e dei programmi, delle scadenze e dei voti, delle rimostranze degli ingegneri del triennio se non ricordano le formule a mente e le definizioni…; il cucciolo dell’uomo ha il diritto di imparare a ‘costruirsi’ i propri modelli razionali, efficaci e graduali, di interpretazione del mondo. E’ solo in questa prospettiva che ha significato l’aggettivo ‘formativo’ che attribuiamo all’insegnamento della fisica al biennio superiore.

Sarebbe interessante a questo proposito compilare una serie di domande opportune che colgano in profondità le strutture di base della fisica formativa del biennio, al di là delle mere nozioni e delle meccaniche esercitazioni spicciole, e con esse preparare un questionario da somministrare agli studenti alla fine del biennio e contemporaneamente alla fine del triennio tecnico raccontando e riflettendo sui risultati comparati. Anni fa, quando insegnavo ancora, feci un tale esperimento aiutandomi nella compilazione anche con questionari sorti in testi specializzati e nelle accademie per analoghi compiti. Da questo mio unico studio risultò, stranamente, che l’insegnamento tecnico con i suoi tecnicismi, meccanismi, espedienti ed artifizi sembrò obnubilare il ragionamento fisico formativo, cioè il pensiero fisico (la Philosophia Naturalis), acquisito al biennio! Sarebbe interessante infatti, per l’insegnamento, se si potesse capire e controllare statisticamente, se davvero questa mera ipotesi fosse da considerare corroborata.

Il sasso aumenta di velocità perché urta la mano che cerca di fermarlo, con più violenza a maggior spazio percorso. Tale sforzo della mano non legato in generale alla prima potenza della velocità, ma alla seconda: noi questo lo sappiamo (anche se dobbiamo far finta di non saperlo; per iperbole, meglio sarebbe direttamente non saperlo, direbbe Foerster!), ma Simplicio non lo può sapere.

Possiamo usare così il criterio di semplicità : la prima ipotesi a questo punto che viene in mente agli alunni è la diretta proporzionalità fra V ed S, proprio come accadde anche allo stesso Galileo! (6).

Quando nella discussione di un problema concludiamo che all’aumentare di una grandezza anche l’altra, alla prima ipoteticamente correlata, aumenta o diminuisce ‘spariamo’ l’ipotesi più semplice di diretta o inversa proporzionalità rispettivamente, a meno che ulteriori approfondimenti della discussione non suggeriscano altrimenti (caso per es., della relazione fra forza gravitazionale e distanza, da affrontare in altro lavoro; vedere intervento dello stesso autore nel blog).

Scrivere oggi V=K*S sembra ‘proibito’ (vedere dopo), per ragioni però troppo lontane dalla mente del nostro alunno Simplicio; comunque essa è la ipotesi più immediata e più vicina al senso comune degli alunni (ed anche a quello di Galileo!) e la dobbiamo mettere nella discussione.

Così la classe, se è vero come è vero che la velocità aumenta anche al passare del tempo, due ipotesi ‘tentative’ saranno formulate dalla classe sul problema della caduta dei gravi, che nelle nostre condizioni al contorno, che riguardano velocità e tempo iniziali, si presenteranno come segue:

1 – La V-istantanea ed S direttamente proporzionali.

2 – La V-istantanea e t direttamente proporzionali.

PRECISAZIONI E SOTTIGLIEZZE CHE SORGONO ARGOMENTANDO SULLE DUE IPOTESI

Non è così immediato intuire per gli alunni che le due ipotesi non sono la stessa cosa. Dobbiamo così rifarci alla matematica elementare del moto uniformemente accelerato (già spiegato in cinematica fra i modelli razionali per ‘leggere’ i diversi moti possibili: se V e t sono direttamente proporzionali (sotto le solite convenzioni al contorno), si dimostra matematicamente e graficamente che V^2 ed S sono direttamente proporzionali e non V ed S, e nel dire V ed S direttamente proporzionali e V e t direttamente proporzionali si vengono ad enunciare due ipotesi diverse e alternative.

Come già accennato anche lo stesso Galileo davanti allo stesso problema formulò proprio le stesse due ipotesi, anche se su V=K*S ebbe in breve dei dubbi. Infatti, dopo avere annunciato tale ipotesi in una lettera a Paolo Serpi, subito dopo, nei “Discorsi e dimostrazioni matematiche”, faceva dire per bocca di Salviati:

“Quando le velocità hanno la medesima proporzione che gli spazi passati o da passarsi, tali spazii vengono passati in tempi uguali: se dunque le velocità con le quali il cadente passa lo spazio di 4 braccia furon doppie delle velocità con le quali passò le prime due braccia, [appartenenti alle 4 precedenti; nota dell’Autore] (sì come lo spazzio e doppio dello spazio) adunque i tempi di tali passaggi sono uguali”

Nello stesso moto si verrebbero a percorrere nello stesso tempo un dato intervallo di spazio e la sua metà, appartenente ad esso cosa che può accadere solo se il movimento è istantaneo (velocità infinita). Il ragionamento di Galileo può essere descritto, dalla tabella successiva, considerando X la velocità media nelle prime due braccia e 2X la velocità media in tutte le 4 braccia e, se t = S/Vm (S/t=Vm con le nostre condizioni al contorno), 2/X è l’intervallo di tempo nelle prime due braccia e 4/(2.X) e l’intervallo di tempo in tutte le quattro braccia

                                       S          Vm                t           CONCLUSIONE

Le prime due braccia      2           X              2/X                   2/X

Le quattro braccia          4           2.X            4/(2.X)              2/X

Si vedano anche le altre più qualificate e profonde argomentazioni sorte ultimamente in ambiente accademico (7) (8).

Il fatto che la discussione galileiana su un problema presenti varie sfaccettature, il fatto che esistano più modi di argomentare sull’ipotesi conseguente non significa che non si debba, come faceva Galileo – non necessariamente allo stesso modo- discutere su problemi per tentare soluzioni prima dell’esperimento. Chi vede in questo pericoli di ambiguo verbalismo, non coglie i significati profondi di un corretto discorso epistemologico e psicologico sui processi di acquisizione della conoscenza e, quello che è più grave, potrebbe sviare gli interventi per il recupero delle situazioni tutt’altro che rosee focalizzate dai diversi tests piagettiani sull’intelligenza formale del giovane di oggi (9) (10).

Consapevolmente o no, Galileo, sempre secondo l’autore dello scritto, dimostra la non coincidenza delle due ipotesi e così faremo nell’insegnamento: si formuleranno le due ipotesi e si dimostrerà in qualche modo che sono diverse e alternative se è ‘vera’ l’una , non lo sarà l’altra e viceversa.

Si passerà poi a controllare in laboratorio se è corroborata l’ipotesi V/t=K, che fornisce come proposizione sperimentabile S/t^2=K. Con l’asserzione-base S=t^2*K che è appunto la formulazione meglio sperimentabile di V/t=K, andiamo in laboratorio per il controllo. In realtà l’ipotesi in un certo ‘range’ di errore è corroborata.

Siamo così arrivati a concludere che l’oggetto (per es., una sferetta d’acciaio, se si utilizza un’apparecchiatura Leybold) cade di moto uniformemente accelerato e quindi la relazione fra velocità e spazio è del tipo V^2/S=K, moto matematicamente e fisicamente possibile, mentre la relazione V=K*S rimane esclusa sperimentalmente. L’ipotesi V^2/S=K però non era così semplice come l’altra, per cui non veniva formulata in prima istanza. Chiaramente le due ipotesi V=Kt e V^2=K*S sono fisicamente la stessa cosa.

Rimangono ora da precisare alcune sottigliezze implicate nel significato di K e quindi formulare il nuovo problema da affrontare nella successiva unità didattica. Prima però analizziamo brevemente il significato matematico e fisico della ipotesi V/S=K e V^2/S=K

ALCUNE CONSIDERAZIONI FISICO-MATEMATICHE SULL’IPOTESI V=K*S

Analisi matematica e fisica dell’ipotesi V=K*S

L’ipotesi è espressa dall’eq. differenziale a variabili separabili: dx/dt=K*(x-x₀). Dall’analisi di essa, forse impossibile ai tempi di Galileo o meglio che Galileo non conosceva, deriva che, per la ricerca delle soluzioni è necessario porre la condizione che (x-x₀) > < 0, perché, separando le variabili (dx/(x-x₀) =K*dt) questa differenza va al denominatore, per cui nel processo si perderebbe la soluzione matematica (che invece (fisicamente) potrebbe esistere?), (x-x₀)=0 m.

___________________________________

Possibile significato della soluzione (x-x₀)=0 (argomentazione incerta? Da rifletterci!)

Galileo_VfS

All’istante t=0 s quando x=x₀ la velocità è zero e, non potendo aumentare x, non aumenta V, per cui x=x_o rimane costante al passare del tempo e l’oggetto non si muove. Invece l’eq. dx/dt=K*t fornisce ancora per t=0, V_o= 0 m/s, però il tempo scorre, per cui la V può aumentare.

x=x_o sembra così essere l’unica soluzione: a t=0, ovunque, del percorso x, poniamo l’origine dello spazio x_o , l’oggetto ivi in quiete (V_o=0 m/s), lasciato andare, rimarrebbe in quiete (se vogliamo, si dovrebbe attendere cioè un tempo infinito per vederlo iniziare a muoversi).

IN FORMULE

dx/dt = k.x   separando le variabili:   dx/x = k.dt; integrando:    logx = k.t + logC; passando agli esponenziali:   e^logx = e^(k.t + logC),  e , ponendo C1=e^logC :

e^logx=e^kt . e^logC)

x=C1.e^kt

Se x=xo al tempo t=0, si ha che C1=xo ed      x=xo.e^kt

Se,  al tempo t=0, x=xo=0  e C1=0, si conclude che:

x = 0. e^kt e quindi      x=0

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

Non esistono altre soluzioni fisiche all’equazione, perché l’integrazione per il calcolo dello spazio (equazione oraria) non può partire dal punto x_o (distanza dall’origine a t=0 s), non permettendo quindi la scelta arbitraria (convenzionale) delle origini; si otterrebbe infatti, integrando l’equazione  dx/(x-x₀) =K*dt  fra x_o ed x, la seguente espressione, chiaramente inaccettabile:

log(x – x_o) – log(0) = K*t

---

Analisi matematica e fisica dell’ipotesi V^2 = K*S fornisce un modello fisico che funziona

L’analisi matematica dell’ipotesi V^2 = K*S fornisce un modello fisico che funziona:

(dx/dt)^2 = K*(x-x₀)

dx/dt = +/- SQR (K) * SQR (x-x₀)

Separando le variabili e integrando fra x₀ ed x:

2*SQR (x-x₀) – 0 = +/- SQR (K)*t

Elevando al quadrato:

4 * (x-x₀) = K * t^2

---

N.B. Dopo aver letto i due  links, tornare indietro all’articolo (cliccando sulla freccia in alto a sinistra)  per leggere l’ultima parte dell’articolo!

Per ulteriori chiarimenti e precisazioni si aggiungono in link anche le due argomentazione indipendenti di Giorgio Cellai e Pier Francesco Bianchi sulla soluzione della stessa equazione differenziale a variabili separabili:

dx/dt=K*(x-x0)

Argomentazione di Giorgio Cellai in pdf

Cellai 18-2-19

Argomentazione di Pier Francesco Bianchi in pdf

GALILEO_Pf_Bianchi0001

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

Ma, al di là di tutto ciò che insegna Galileo, è il modo scientifico formativo di condurre il processo, il modo di discutere il problema, sezionandolo con tutti gli strumenti razionali conosciuti per chiarirlo e ‘sparare’ infine un tentativo di soluzione: ciò che insegna Galileo in definitiva è il modo corretto di fare lezione in una classe in cui si formano i cervelli!

FASI SINTETICHE DEI PROCESSI RAZIONALI, ‘RICCHI’ DI TRANSFER, NELL’ANALISI DEL SIGNIFICATO DELLE COSTANTI DI PROPORZIONALITA’

In generale le fasi del processo razionale davanti ad una ipotesi di diretta proporzionalità, corroborata nell’ambito dell’errore, possono essere brevemente delineate in questo modo:

1 – La grandezza derivata K non dipenderà dalle grandezze che lega, ma da altre relative a ‘qualcosa’ di rilevante che durante l’esperimento non è cambiato.

Se, in dinamica, F/a = K, il valore di K non dipenderà dalla grandezza della variabile accelerazione né dalla grandezza della variabile forza (almeno nel ‘range’ dell’errore sperimentale) e quindi potrebbe dipendere da qualche grandezza relativa all’oggetto con cui abbiamo sperimentato che immaginiamo invariato durante l’esperimento. Da quali?

Se, in elettrodinamica, (Va – Vb)/Ic = K, il valore di K non dipenderà dalle grandezze elettriche differenza di potenziale e intensità della corrente; è facile riferirci allora a qualche proprietà del conduttore su cui abbiamo sperimentato. Da quali?

Se, in elettrostatica, Q/V = K, il valore di K non dipenderà dalle grandezze eletrostatiche carica elettrica e potenziale elettrico, ma da qualche proprietà del conduttore dell’esperimento. Da quali?

2 – Il significato fisico di K nasce poi dal metterci, anche mentalmente, nelle condizioni di ripetere l’esperimento ottenendo un valore di K diverso.

Se il K di F/a dipende dall’oggetto su cui abbiamo sperimentato, immaginando un oggetto diverso, se K verrà maggiore, a parità di forza applicata, a acquistata sarà minore; cioè K dipenderà da una proprietà dell’oggetto che si configura come ostacolo all’accelerazione. Potrebbe essere già stata introdotta una grandezza fondamentale che misuri tale proprietà con la bilancia inerziale (al limite una molla tenuta compressa da un filo), con cui si può attribuire un numero e marca  alla massa Inerziale (vedere dopo).

Se il K di (Va-Vb)/Ic dipenderà da qualche proprietà del conduttore usato, cambiandolo otterremo un K diverso. Se è maggiore significherà che, per es., a parità di differenza di potenziale avrò una Ic minore: K si configura come una specie di ostacolo al passaggio della corrente (resistenza elettrica). Una successiva discussione potrà precisare la dipendenza di K dalle grandezze geometriche del filo ecc. Si innescherà una successione di problemi a cascata da affrontare in successive unità didattiche.

Se k di Q/V dipende dal conduttore caricato, cambiandolo dovrebbe cambiare K: se K è maggiore significherà che posso mettere su tale conduttore più carica, a parità di potenziale; cioè K potrebbe avere il significato di capacità elettrica di quel conduttore. Una successiva discussione preciserà la dipendenza da altre grandezze e così via.

3 – Precisazione concettuale delle grandezze investigate.

Come si vede si tratta di veri e propri processi razionali che si ripetono in ambienti diversi, favorendo il transfer concettuale all’interno della disciplina (transfer specifico di Bruner), attraverso il potente Principio di Continuità galileiano.

ASPETTI RELATIVI AI SIGNIFICATI DELLA COSTANTE DI PROPORZIONALITA’ FRA V e t

Abbiamo corroborato in laboratorio l’ipotesi V/t = K: K ha le dimensioni di una accelerazione, e, proprio perché non cambia durante il movimento, non dipenderà dalla V, né dal tempo che cambiano. Potrei così, nella falsariga degli esempi accennati nel paragrafo precedente, affermare che K venga a dipendere da qualche proprietà dell’oggetto usato per l’esperimento. Tale congettura è plausibile abbastanza a questo stadio: oggetti più o meno ‘pesanti’, per es., potrebbero avere accelerazioni di caduta diverse….Cioè dire che K dipende da qualche proprietà dell’oggetto, può voler significare, per es., che oggetti più ‘pesanti’ cadrebbero con un K maggiore (è la congettura più frequente nelle classi, a causa dei riferimenti all’esperienza quotidiana).

Nasce così il nuovo problema sul significato di K ed eventuali ulteriori problemi sulla sua dipendenza da qualche altra grandezza.

Formuliamo, per es., l’ipotesi che sperimentando con un oggetto più ‘pesante’, il K diventi maggiore: oggetti più ‘pesanti’ cadrebbero allora con maggiore accelerazione?

Lasciamo in questa fase, la discussione ad un livello basso, per sfruttare la delusione onde focalizzare l’interesse e destare ‘meraviglia’. Volendo potevamo approfondire usando anche il Teorema di Galileo sull’argomento (nota n.11), eliminando praticamente il rischio sull’ipotesi.

La classe segue motivata il nuovo esperimento sulla misura di K nella caduta e la delusione delle aspettative lascia piuttosto perplessi: la proprietà o le proprietà dalle quali sembrava dipendesse il nostro K sembra non siano relative all’oggetto scelto per l’esperimento.

Seguiranno successivamente argomentazioni insieme alla classe sui presupposti che hanno portato alla formulazione dell’ipotesi sbagliata. A questo punto possiamo anche inserire il teorema galileiano, per tranquillizzare nell’immediato la classe. Si potrà continuare anche a precisare i concetti coinvolti sperimentando col Tubo di Newton.

La discussione dovrà poi procedere facendo riferimento a dati riportati di libri e riviste: si conclude che “tutti i corpi in assenza di attrito cadono, nello stesso posto, con la stessa K (stessa accelerazione)”. Così sembra importante anche il ‘posto’, la zona di spazio dove si esegue l’esperimento, quasi che le ‘zone di spazio’ influiscano in un certo modo sulle proprietà dell’oggetto usato, spostandoci a giro per universo.

I corpi celesti infatti deformano lo spazio con una grandezza vettoriale chiamata ‘campo gravitazionale’. Il comportamento del nostro K potrebbe essere modificato proprio da tale campo: quindi l’oggetto, le cui proprietà non cambiano durante l’esperimento in un dato posto, ha a che fare anche con il corpo planetario nelle vicinanze, nella fattispecie la Terra (il ‘pesare’ degli oggetti non è forse una funzione dei campi gravitazionali nelle vicinanze?). Così il valore del nostro K risentirà di proprietà forse  intrinseche – proprietà di opporsi a K o proprietà di attrarre e farsi attrarre, cioè di ‘costruire’ K – all’oggetto usato per l’esperimento (o forse potrebbero costruirsi’ in interazione con ‘aspetti’ dello spazio vicino e lontano? Mach, Newton). Proprietà insomma che 1) ora ne ostacolano il suo valore (massa inerziale, misurabile con un bilancia inerziale), 2) ora lo aumentano (peso e mass gravitazionale, misurabili con un dinamometro opportunamente tarato e con una bilancia a bilico) – i due aspetti precedenti ne controllano la sua strana costanza, aspetto caratteristico del nostro Universo – 3) ora che dipendono dal ‘posto’ dell’esperimento, pur mantenendo la sua costanza per tutti gli oggetti usati. Il peso degli oggetti ha a che fare con la legge gravitazionale di Newton.

Newton affermava che esistevano almeno due tipi di proprietà intrinseche ad un ogni oggetto fisico collegate al concetto di massa: la massa inerziale, che rappresenta la proprietà di opporsi allo stato di quiete e moto rettilineo uniforme, cioè alla accelerazione, e la massa gravitazionale, proprietà invece di farsi accelerare e creare accelerazione in interazione con altri oggetti. Concettualmente, pur interne all’oggetto, le due masse sono concettualmente disgiunte, nel senso che non sono collegate logicamente da una argomentazione teorica; infatti le rispettive grandezze nascono da due esperimenti di misura completamente diversi. La massa inerziale utilizza per la misura una esperimento che fa riferimento al Terzo principio della dinamica, Principio di Azione e Reazione, mentre la massa gravitazionale si misura con una bilancia a bilico. Queste due misure sperimentali, di natura concettuale completamente diversa, con scelta opportuna delle loro unità,  risultano numericamente uguali per qualsiasi oggetto: una stranezza caratteristica del nostro Universo! Allora si disse: E’ così perché è cosi!
La uguaglianza numerica di esse per ogni oggetto fisico poteva essere ricavata più semplicemente anche con un ragionamento argomentativo (Newton) partendo dalla costanza dell’accelerazione di gravità g, per es., in un zona limitata dello spazio intorno alla terra, non solo durante il moto, ma per qualsiasi tipo di oggetto di qualsiasi natura. Se lascio cadere in una piccola zona un qualsiasi un oggetto di qualsiasi natura e grandezza, per le due definizioni di massa e per il Secondo Principio della Dinamica, l’oggetto, sottoposto alla sua forza peso P che, nel nostro caso, rimane circa costante per ogni oggetto durante il moto, ma varia da oggetto a oggetto, crea una accelerazione a costante per ogni oggetto, ma non è detto che abbia lo stesso valore passando da un oggetto ad un altro se P cambia. In effetti alla accelerazione finale contribuiscono i due contributi delle due masse:

a1=kMg e a2=k’/Mi

Poichè a1 è un incremento e a2 è un decremento sull’accelezazione finale, i due contributi devono essere uguali, se l’acc. finale rimane costante (accelerazione di gravità) per tutti gli oggetti in caduta, cioè g, per l’ ipotesi iniziale.

Qualsiasi oggetto prendo, per l’uguaglianza di g, a1=a2 per cui kMg=k’Mi; ne deriva kMg/k’Mg=1 e quindi, se k=k’ (opportuna scelta delle unità di misura, per le due masse), ottengo Mg=Mi. Basta si consideri che l’oggetto campione  per la massa corrisponda ad una unità di Mi e una di Mg? La differenza numerica delle due masse all’interno degli oggetti risultò dell’ordine di 10^-12. [ Nel blog, cercare “Tao…”, nota (***), ancora di Piero Pistoia].

Il problema diventa complesso: potrà o non potrà essere sviscerato in tutte le sue parti a seconda dei livelli di comprensione e di impegno delle classi di un biennio superiore.

Una cosa è certa: a più di quattro secoli da Galileo dobbiamo esser contenti se si trova ancora nelle nostre scuole, nonostante i mass media, i personal media…, qualche Simplicio che fa ancora le stesse domande ingenue a fronte degli stessi problemi e quasi allo stesso modo.

Rimane da chiederci se la nostra pesante cultura del periodo post-industriale e tecno-ragionieristico, con i suoi prodotti tecnologici così sofisticati fuori della scuola ed anche dentro la scuola (rotaie a cuscinetto d’aria, cronografi ad 1/1000 di sec…), non possa creare nella mente impressionabile dei nostri ragazzi, sovrastrutture così artificiose da impedire i livelli di maturazione normale ed il formarsi graduale di modelli calibrati di interpretazione del mondo (gradualmente sempre più simbolici) e quindi lo sviluppo armonico dell’intelligenza (9) (10).

NOTE E BIBLIOGRAFIA CONSULTATA

1 – K. Popper “Logica della scoperta scientifica”, Einaudi,1970; K. Popper “Conoscenza oggettiva”, Armando, 1975; P. Feyerabend,T.Khun, I. Lakatos et al. “Critica e crescita della conoscenza”, feltrinelli, 1976; D. Antiseri “Epistemologia e didattica delle scienze”, Armando, 1977; P- Redondi “Epistemologia e storia della scienza”, Feltrinelli, 1978.

2 – J. Piaget e B. Inhelder “De la logique de l’enfant e la logique de l’adolescent”, Puf Paris, 1955; J. S. Bruner “Lo sviluppo cognitivo”, Armando, 1973; J. S. Bruner “Il significato dell’educazione”, Armando, 1973; R. Mazzetti “Dewey e Bruner”, Armando, 1976.

3 – J. S. Bruner “Verso una teoria dell’istruzione”, Armando, 1967; M. Laeng “L’educazione nella civiltà tecnologica”, Armando, 1969; P. Pistoia, A. Pazzagli “I fondamenti psicologici ed epistemologici dell’insegnamento della fisica”, La ricerca,15-12-1977, Loescher; P. Pistoia, A. Pazzagli “I processi di e la loro utilizzazione per l’insegnamento della fisica”, La Ricerca, 15-11-1978, Loescher; A. Pazzagli, P. Pistoia “Alcuni presupposti psicopedagogici ed epistemologici della riforma della scuola superiore”, La Ricerca, 15-3-1980, Loescher.

4 – P. Wiener e A. Noland “Le radici del pensiero scientifico”, Fltrinelli, 1977; per non parlare dell’analisi del pensiero galileiano condotta da Feyerabend in “Problemi dell’empirismo”, Milano, 1971 e in “Contro il metodo”, Milano, 1973.

5 – P. Pistoia “Considerazioni critiche su un progetto programmatico relativo al processo di comprensione di una concetto fisico”, La Ricerca, 15-10-1981,Loescher.

6 – G. Galilei “Discorsi e dimostrazioni matematiche”, Salani, 1964.

7 – S. Bergia, P. Fantazzini “La Fisica nella scuola”, XIII, N.1, 1980.

8 – Elio Fabri “La fisica nella scuola”, XIV, N.3, 1981.

9 – L. Bergamasco “Didattica e sviluppo intellettuale degli studenti” da ‘Il giornale di fisica’, gennaio-marzo, 1977.

10 – P. Violino e B. Di Giacomo “ Sul livello cognitivo degli alunni delle scuole secondarie superiori” da ‘la fisica nella scuola’, luglio-settembre, 1981

11 – G. Galileo “Ma questo è, ed è insieme vero che una pietra grande si muove, per esempio, con 8 gradi di velocità, ed una minore con quattro, adunque congiungendole ambedue insieme, il composto di loro si muoverà con velocità minore di otto gradi; ma le due pietre, congiunte insieme, fanno una pietra maggiore che quella prima, che si muoveva con 8 gradi di velocità; adunque questa maggiore si muove meno velocemente che la minore che è contro vostra supposizione”

In effetti Galileo fece ben pochi esperimenti; qualcuno ha detto che forse ne fece uno solo, quello sul piano inclinato ( Galileo’s ? experiment: Myth and symbol, da Rogers “Physics for inquiring mind”, Princeton ). Galileo era un fisico teorico piuttosto che uno sperimentale. Egli usava l’argomentazione logica  in esperimenti pensati e il principio di continuità, individuato in lui da Mach, per cui si mantiene la struttura concettuale, variando lentamente, con continuità appunto, gli elementi sperimentali. Se oggetti di diverso peso (gravi) cadevano dalla stessa altezza, dovevano toccare terra con la stessa velocità, altrimenti si manifestava una contraddizione. Ammettendo che il più peso avesse velocità maggiore, collegandolo all’altro più leggero, questo oggetto composto complessivamente, più pesante di ognuno dei due, avrebbe dovuto possedere una velocità ancora maggiore rispetto al più pesante da solo. La contraddizione nasce perché, nella combinazione dei due, il leggero, a sua volta, avrebbe dovuto rallentare invece il più pesante e quindi la velocità finale dell’oggetto composto avrebbe dovuto essere in effetti minore del più pesante da solo. E’ interessante notare che la velocità, uguale per tutti i gravi, derivata logicamente, rimandi ad una proporzionalità “nascosta e profonda” fra massa gravitazionale ed inerziale per tutti gli oggetti dell’universo fisico. Sembra così che esista un legame fra il ragionamento logico, in esperimenti pensati con oggetti fisici, e le leggi profonde. Se le leggi al di sotto delle apparenze non fossero così, si potrebbero verificare contraddizioni logiche da qualche parte del mondi fisico.

Piero Pistoia

Da continuare….

LEZIONI DI FISICA del dott. prof. Giorgio Cellai

Lezione di elettrodinamica n° 1

LEZIONE DI FISICA 1: IL CIRCUITO ELEMENTARE E FORZA ELETTROMOTRICE

Dott. Prof. G. Cellai

 

Per leggere articolo in doc, cliccare su:

IL CIRCUITO ELEMENTARE 1

Per leggere articolo in pdf cliccare su:

circuito-elementare-2

___________________________

 

Lezione di Elettrodinamica 2

LEZIONE DI FISICA 2: MODELLO VISCOSO E LEGGI DI OHM

Dott. Prof. G. Cellai

 

CELLAI_Modello viscoso Sillabario.pdf

 

ALCUNE LEZIONI DI FISICA RELATIVISTICA, a più voci; dott. prof. Rosa-Clot, dott. prof. F. de Michele, dott. prof. G. Cellai, dott. P. Pistoia; post aperto

Testo rivisitato da “il Sillabario”, n. 2 1996

Testo rivisitato da ‘Il Sillabario’, n. 3 1996

Testo rivisitato da ‘Il Sillabario’, n. 4 1997

Testo rivisitato da ‘Il Sillabario’,  n. 1 1998

IL PARADOSSO DEI GEMELLI?

Dott. Prof. Marco Rosa-Clot

Fisico Teorico, Università di Firenze

“Sono convinto che i filosofi hanno sempre avuto un effetto dannoso sul progresso del pensiero scientifico poiché hanno sottratto molti concetti fondamentali al dominio dell’empirismo, nel quale si trovavano sotto il nostro controllo, e li hanno portati alle intangibili altezze dell’“a priori “.

Questa frase polemica e di sapore vagamente oscurantista apre il famoso libro di Einstein “Il significato della relatività” in cui viene esposta in modo conciso e compiuto, la teoria della relatività galileiana, speciale e generale (il lettore non si faccia illusioni: il libro è un capolavoro di chiarezza ma richiede approfondite conoscenze di geometria differenziale ed è tutt’altro che accessibile ai non specialisti).

Sorvoliamo sulla polemica, evitiamo di richiamare l’importanza per la storia del pensiero umano della speculazione filosofica, e umilmente seguiamo la lezione empirista.

Saliamo su un aereo, controlliamo l’orologio. Partiamo da Roma e facciamo rotta equatoriale verso Tokyo. Io passando da Bombay e voi da NewYork. A Tokyo prendiamo un caffè e poi continuiamo il nostro viaggio (ognuno nella sua direzione) per poi ritrovarci a Roma allo stesso punto a  circa due giorni dalla partenza.

Controlliamo gli orologi: il mio orologio (ho viaggiato verso est) segna un tempo maggiore del vostro. Vi posso assicurare che i due orologi sono identici, che funzionano benissimo, non c’è trucco. Se partendo avevamo la stessa età ora voi siete in realtà un po’ più giovani di me. Mica di tanto si capisce; controllando bene si tratta di soli 300 nanosecondi, cioè 0,3 milionesimi di secondo; ma siete più giovani! Questo è il punto.

Quello che ho descritto è in effetti l’esperimento di Hafele e Keating (due fisici americani) del 1971. I due aerei scelti per l’esperimento hanno volato per circa 50 ore e i due orologi erano due orologi atomici identici in grado di apprezzare il miliardesimo di secondo (il nanosecondo).

La teoria della relatività prevedeva in questo caso una differenza di tempi di 315 ±30 nanosecondi (miliardesimi di secondo), il risultato sperimentale trovato fu  di 332±12 ns. Un successo straordinario dell’analisi teorica di Einstein di più di mezzo secolo prima. Un risultato giudicato dai contemporanei prima manifestamente falso e poi paradossale: il paradosso dei due gemelli.

All’epoca fu infatti proposto un “gedenken experiment” (un esperimento pensato): uno dei due gemelli intraprende un viaggio spaziale a velocità prossima a quella della luce e quando ritorna trova il fratello molto più vecchio di lui: il tempo e passato in modo diverso per i due soggetti.

Hafele e Keating hanno realizzato questo esperimento utilizzando i mezzi di trasporto disponibili e migliorando enormemente il sistema di misura del tempo: non si guardano i capelli bianchi di un uomo ma si contano le oscillazioni degli atomi di cesio di un orologio atomico.

Ma perché parlare di paradosso?

E’ paradossale che una trottola in rapida rotazione non cada e si mantenga in equilibrio sulla sua punta?  Dipende dai punti di vista ma soprattutto dall’abitudine. Fin da bambini abbiamo visto trottole girare e ora ci sembra del tutto naturale che ciò avvenga. Inoltre le leggi della meccanica del corpo rigido spiegano benissimo questo fenomeno in tutti i suoi dettagli.

E’ paradossale che un aereo voli? Forse, ma a partire dagli studi di Leonardo e dalle sue osservazioni sul volo degli uccelli lo è un po’ meno, e oggi è certamente considerato un fatto quanto meno ovvio; anzi è paradossale che un aereo cada.

Continuiamo a seguire umilmente la lezione empirista e poniamoci una prima domanda: cosa è il tempo? (dal punto di vista fisico si intende, non soggettivo o meteorologico od altro).

La fisica considera il tempo in modo empirico come una grandezza continua, misurabile con orologi, e che scorre in una sola direzione.

L’individuazione di un evento avviene assegnandone le coordinate spaziali e l’istante temporale in cui si verifica. La principale differenza tra posizione e tempo sta nella possibilità di muoversi lungo le coordinate in ogni direzione mentre il tempo è per sua natura unico e percorribile solo in un senso.

La fisica assegna anche leggi di trasformazione delle coordinate che sono deducibili da osservazioni sperimentali. Per esempio l’osservazione empirica comune ci insegna che la posizione di un viaggiatore su un treno in movimento con velocità v rispetto a un amico fermo in stazione sono date da x’ = x_o + vt dove x_o è la sua posizione all’istante t=0 (trasformazione della relatività galileiana), mentre il tempo per i due amici è lo stesso: t’ = t.

La fisica relativistica, a partire dall’osservazione che la velocità della luce nel vuoto è invariante a prescindere dal sistema di riferimento in cui viene misurata, arriva ad altre relazioni: le trasformazioni di Lorentz.

Certo è paradossale affermare che la velocità della luce è la stessa sia che il raggio luminoso parta da un treno in corsa che dall’osservatore fermo. Per la bottiglia di gazzosa lanciata dal finestrino non è certo la stessa cosa: in un caso il signore in stazione la lascia cadere correttamente nel cestino dei rifiuti, nell’altro il passeggero sul treno in corsa la lascia cadere dal finestrino e il risultato può essere disastroso.

Tuttavia i fotoni non sono bottiglie di gazzosa e potremmo dire che sarebbe piuttosto paradossale trattarli alla stessa stregua.

Allora seguiamo ancora la lezione dell’empirismo ed accettiamo che c è costante. Paradossale ma vero, quindi non paradossale. Se prendiamo la parola nel suo etimo (al di là dell’opinione) c = costante in ogni sistema di riferimento è una realtà fisica e quando ci si abitua a questo, per definizione non è più paradossale.

L’implicazione delle trasformazioni di Lorentz sull’intervallo temporale sono semplici:

e ricordando che dx = vdt

che per velocità v piccole rispetto a c si può scrivere

Questa formuletta merita di essere illustrata in un grafico.

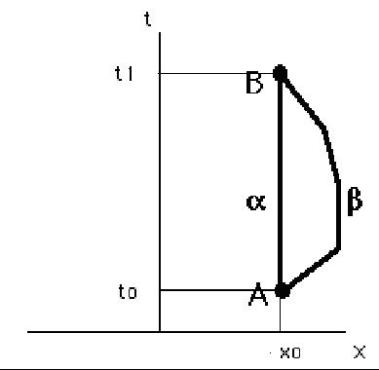
Supponiamo di studiare due diversi percorsi nello spazio tempo (vedi fig. 1).  In un primo caso (cammino a) il soggetto a sta fermo nella posizione x=x_o

e si trova dopo un tempo Dt  nella stessa posizione senza mai muoversi. Nel secondo caso (cammino b) il soggetto b si allontana dalla posizione originaria per poi tornarci. Nel far questo il suo tempo cambia secondo la legge:

enunciata sopra  e quindi quando torna al punto B il suo tempo risulta minore! la linea retta tra due punti nello spazio tempo della relatività risulta essere la più lunga possibile rispetto a qualsiasi altra congiungente!

Figura 1: Rappresentazione schematica del percorso dei due gemelli che vanno dal punto A (di coordinata xo) al punto B (stessa coordinata spaziale) lungo due diversi percorsi. Percorso a : il gemello 1 sta fermo e lascia passare il tempo da t_o a t₁. Percorso b: il gemello 2 si allontana da x_o per poi ritornare a x_o e ritrovarsi con il gemello 1 al punto B all’istante t₁.

Paradossale! ma vero e inoltre osservato (quindi non paradossale).

Si noti che il tempo proprio dei due osservatori non viene alterato; gli orologi atomici non rallentano o accelerano e (ciascuno nel suo sistema) soddisfano immutati le stesse leggi della fisica atomica e dell’elettromagnetismo. Cambia la distanza di tempo relativa. Inizialmente nulla, essa aumenta progressivamente fino a diventare 330 ns alla fine del viaggio.

Per comprendere meglio il fenomeno serviamoci di una analogia: due esploratori all’equatore si trovano alla distanza di 100 Km e si mettono entrambi incammino verso Nord (si noti muovendosi “parallelamente” e su un percorso rettilineo perpendicolare all’equatore stesso). Dopo 100 Km misurano la loro distanza e scoprono che si e’ ridotta di 31 cm. Se continuassero nel loro percorso vedrebbero la loro distanza ridursi ancora sempre più rapidamente fino a diventare zero nel punto di incontro al polo.

La risposta a questa osservazione può essere un sorrisetto di sufficienza: grazie! Sappiamo tutti che la geometria della sfera e’ tale che due meridiani si avvicinano e poi si incontrano  (due archi di cerchio massimo, cioè due parallele). Abbiamo solo scoperto che le leggi di trasformazione delle coordinate non sono quelle del piano euclideo.

Torniamo all’esperimento di Hafele e Keating. In un caso la velocità dell’aereo si somma a quella di rotazione della terra (viaggio orario verso ovest) nell’altro caso si sottrae. e da cui:

Δτ₁ = dt [1+(v_T+v_a)²/c² ]^1/2;  Δτ₁=Δ t v_Tv_a/(2c²)]  e

Δτ₂ = dt [1 + (v_{T –} v_a)²/(2c² )];  Δτ₁ – Δτ₂ =4Δ t v_Tv_a/(2c²)

Ma v_T=  ωR  dove  ω  è a velocità di rotazione terrestre (ω  = 2π/ N_s  dove N_s e’ il numero di secondi in un giorno: N_s  = 8600 sec  e R è il raggio equatoriale e  Δtv_a=2πR . Quindi Δτ₁ – Δτ₂ =4πωR²/c² , circa uguale a 400ns.

Quindi Utilizzando il percorso effettivamente fatto dagli aerei (non seguivano orbite esattamente equatoriali) si trova il risultato citato sopra.

Se queste poche righe hanno lasciato pensare che la frase di Einstein sui filosofi sia da me condivisa chiedo venia al paziente lettore. Spero invece che il discorso sull’empirismo sia accettato nella sua globalità.

Certo la relatività non ci mette a disposizione un metodo per ringiovanire (il tempo scandito dagli orologi atomici scorre inesorabile nei due sistemi di riferimento) ma sicuramente possiamo abbreviare i viaggi spaziali.

Da questo punto di vista l’ignoranza della relatività da parte dell’equipaggio della Enterprise è sconfortante. Questa benedetta astronave si ostina a viaggiare a velocità superiore a quella della luce e ad usare una fisica non relativistica. Orbene, la galassia ha un diametro di 100mila anni luce. Che me ne faccio di una astronave che viaggia 100 volte più veloce della luce e ci mette 1000 anni a raggiungere i Klingoni in capo alla galassia.

Ben altra lezione ci viene dal mondo reale. Arrivano regolarmente sulla terra raggi cosmici con energia di milioni di TeV (tera electronvolt). Un protone con una energia di un milione di TeV (10¹⁸ ev) ha un velocità molto vicina a quella della luce (0.9999999999999999995*c : ci sono 18 cifre 9 dopo lo zero). Ma quello che più interessa è che il rapporto tra il suo tempo e quello di un osservatore fermo è dato da:

che è uguale dt/10⁹.

Quindi in poco più di mezz’ora (del suo tempo proprio) il protone attraversa la galassia e in 10 anni l’intero universo. Povero Star Trek! E questa è fisica!

(Marco Rosa-Clot, fisico Teorico)

(Rivisitato da Il Sillabario, n.4, 1997, XI)

PER VEDERE IL CURRICULUM DI MARCO ROSA-CLOT CLICCARE SU:

mrcsh-it-1

 

 

______________________________

Vedere anche “Un possibile racconto sulla relazione fra massa ed energia” di Piero Pistoia; nell’intenzione, a taglio più didattico argomentativo.

PROLOGO ALL’ARTICOLO di Piero Pistoia

In via di sviluppo; rivisitato e corretto da Il Sillabario n. 4 1995; da esso in particolare riprese le immagini.

Alcune argomentazioni su dubbi!

L’ARGOMENTAZIONE SVILUPPATA IN QUESTO RACCONTO CERCA DI SEMPLIFICARE IL PERCORSO CONCETTUALE SEGUITO NEL TESTO “PHYSICS FOR THE INQUIRING MIND” BY ERIC M. ROGERS, Princerton University press, Cap. 31. Tale testo al tempo fece epoca. Il capitolo 31 sulla Relatività fu poi tradotto anche in italiano per il “The Project Physics Course” della Zanichelli, Unità 4 e Unità 5, 1982. Questa traduzione fu inserita nella Prima Lettura, pagg. 5/114-5/141.

AFFERMAZIONE DI ROGERS NEL CUORE DELL’ARGOMENTAZIONE

“…Then ε, watching ε’  at work, sees that ε’ uses a clock that runs slowly (but they agree on normal meter sticks in the y-directions). So ε sees that when ε’ said  he misured 3 meters travel in 1 sec, it was ‘really’ 3 meters in more-than 1-second  as ε would misure it by his clock…” by Rogers pag. 486

 

___________________________RIQUADRO_______________________

CAPITOLI

  2 – NOZIONI NECESSARIE DI FISICA ELEMENTARE

  3 – NOZIONI NECESSARIE DI RELATIVITA’ RISTRETTA

  4 – RELAZIONE FRA MASSA ‘A RIPOSO’ E MASSA IN MOVIMENTO: UN    ESPERIMENTO “PENSATO” ALLA GALILEO

  5 – LA RELAZIONE FRA MASSA ED ENERGIA

  6 – NOTE

 7 – IL DUBBIO

____________________________________________________________

CLICCANDO SOPRA GLI SCRITTI  POCO LEGGIBILI SI INGRANDISCONO

CENNI DI NOZIONI NECESSARIE DI RELATIVITA’  RISTRETTA

I Postulati della Relatività Ristretta di Einstein affermano 1) Tutte le leggi fisiche sono le stesse in tutti i sistemi di riferimento inerziali (“spazi” che traslano reciprocamente di moto rettilineo uniforme). 2) la velocità della luce (nel vuoto) è la stessa per ogni osservatore in un sistema di riferimento inerziale, qualunque sia il moto relativo fra la sorgente luminosa e l’osservatore. Su questi postulati si “costruiscono”, senza grandi difficoltà matematiche (a parte qualche sottigliezza concettuale), le così dette Trasformazioni di Lorentz (quelle di Galileo riguardavano lo stesso argomento senza considerare il  2° postulato), che rappresentano le relazioni fra coordinate di uno stesso evento “lette” da due osservatori  situati in due “zone di spazio” che si muovono relativamente di moto rettilineo uniforme con velocità V. Senza entrare nel merito, queste trasformazioni permettono di affermare fra l’altro che a)  Ogni osservatore di un sistema inerziale pensa di essere in quiete e vede gli oggetti sull’altro sistema scorciarsi nella direzione del moto  di un fattore 1/R=√(1-V²/c² ) se R=(1-V²/c²)^-1/2. R è anche circa uguale a:  1+1/2*V²/c² .  Se V è minore di c (oggetti-massa), R è maggiore di 1; in buona approssimazione è 1 se V è molto minore di c (V<<c); √(1-V²/c² ) < 1. b)  Ogni osservatore  che pensa di essere in quiete (es., Oa), vede rallentare  l’orologio dell’altro sistema (Ob) ancora di un fattore R. Per Oa rallentano anche le vibrazioni degli atomi e quindi anche gli orologi atomici, il battito del cuore, il metabolismo degli organismi viventi, che probabilmente condiziona tutto il processo vitale (il ciclo vitale degli organismi aumenta insieme alla speranza di vita; si invecchia più lentamente [ha senso qui la relazione Δtb = Δta * √(1-V²/c² )].   Ad ogni intervallo fra ticks successivi corrispondente ad un secondo letto nell’orologio dell’osservatore che pensa di essere in quiete, corrisponde più di un secondo nell’orologio di Ob (per ogni secondo → 1 sec*R; 3 sec in Oa, 3*R sec in Ob, sempre registrati da Oa ). In termini di pendolo, se i due osservatori hanno un pendolo che batte il secondo (oscillazione completa in un secondo misurata da ogni osservatore all’interno del proprio sistema), se Oa (in quiete) guarda il pendolo di Ob, vede che, quando il suo pendolo termina l’oscillazione completa (1 sec), l’altro (OB) ha ancora da terminarla. Che cosa accade ad R se V si avvicina a c? E se V supera c? E delle misure  delle dimensioni degli oggetti ? (l=lo/R, vedere (i) e (ii) nella figura sotto) e del tempo? (t=to*R? vedere (iii) nella figura sotto o t=to/R?); ancora da approfondire!.

Come cambiano le misure predette dalla relatività

L’immagine sopra riportata con scritti in inglese  si trova nel cap. 31 pag. 485 del testo “Physics for inquiring mind” di Eric M. Rogers; in italiano si trova invece nelle ‘Letture’ pag, 5/127 del testo “The project Physics Course, Unita’ 5 e Unita’ 6” Zanichelli editore e noi l’abbiamo presa in prestito.

La Figura sotto rappresenta invece un esperimento costruito nella mente, di fatto scarsamente praticabile, ma che pensiamo possa facilitare l’apprendimento del concetto (ipotesi: le due masse rimarranno uguali? Certamente! almeno il  tipo di atomi e il loro numero rimarranno gli stessi). Centinaia sono stati gli scritti sulla relatività di Einstein dopo la sua pubblicazione all’inizio del XX° secolo e altrettanti verranno pubblicati nel corso del nuovo secolo, con i loro obiettivi, i loro percorsi rilevanti,  i loro stratagemmi, le loro ‘fisiologie’ intendo.  Nel nostro caso ci sono due osservatori in due “spazi” paralleli, che si muovono relativamente in verso opposto di moto rettilineo uniforme con velocità relativa V. Ciascun osservatore possiede un oggetto-massa identico (stesso contenuto di materia) posto in quiete su un piano privo di attrito.  Si appoggi ai due oggetti (chi e come non si sa!) un sistema ‘molla compressa-corda’ privo di massa nel momento di incontro, quando i due spazi si trovano di fronte lungo Y e la molla termina l’azione proprio quando gli orologi dei due sistemi segnano zero secondi (sic!). Per la sincronizzazione degli orologi, posti ai nodi di strutture spaziali ‘a tubi innocenti’ ed altro, si rimanda all’articolo di Giorgio Cellai in questo blog. Sono uguali e opposti gli impulsi nei due sistemi e, per come è stata la spinta, per ogni osservatore all’interno del proprio spazio, appena caduta la molla, i due oggetti si muovono lungo la direzione dell’asse y in versi opposti di moto uniforme con uguali quantità di moto. Per la conservazione della quantità di moto vettoriale infatti, sia il vettore M*Va sia il vettore di verso opposto M*Vb continueranno a ‘guardare’ nella direzione dell’asse Y. Per la fisica classica le due velocità dovranno essere le stesse! Ma  misuriamole tenendo conto delle trasformazioni relativistiche accennate! Da notare che, se, per es., l’osservatore A pensa di essere fermo, vede muovere l’oggetto in B lungo la diagonale di lati V e vb (!), il metro lungo X si contrae,  ma noi siamo interessati solo al movimento lungo y. Se due masse Mb e  Ma interagiscono sotto lo stesso impulso, in un sistema isolato, come già accennato, la Quantità di Moto totale è costante nel tempo. Tenendo conto  delle condizioni iniziali (per t=0, vb1=va1=0) otteniamo Ma*va = Mb*vb e se, per l’osservatore A per qualche ragione, vb=va/R, vb diminuisce di R,  per cui Mb=Ma*va/vb aumenta di R.  E viceversa per l’osservatore B. Se partiamo con due masse uguali , Mb=Ma, otteniamo che Mb diventa maggiore di Ma a causa del movimento (ancora da rifletterci)._____________________________RIQUADRO___________________

Per qualsiasi valore di V anche per V/c<<1:

M-Mo = Mo*R – Mo    dove    R=1+1/2*V^2/c^2 ;   se

M-Mo = Mo*(R-1) allora  M-Mo = 1/2 * Mo*V^2/c^2 =Er/c^2

ΔM =Er/c^2

Se V<< c, fornendo energia cinetica  (tramite lavoro  di una forza , urto…) o energia di qualsiasi altro tipo (es., calore), la sua massa , in conseguenza di ciò, aumenta di Er/c^2 e viceversa.  (Da chiarire ulteriormente)

Attenzione: è la V, velocità relativa dei due spazi, che fa rallentare gli orologi, non le velocità delle due masse, indicate con Va e Vb ovvero va e vb o altro! R=1+1/2*V^2/c^2 

__________________________________________________________

Piero Pistoia

N.B. – I DUBBI SU ALCUNI PASSAGGI CONCETTUALI SONO STATI DISCUSSI CON L’ING. RODOLFO MARCONCINI E COMUNICATI ANCHE AL  PROF. GIORGIO CELLAI.

IL DUBBIO:  Dai principi della Teoria è possibile derivare logicamente in ogni caso la seguene relazione?

 Δtb = Δta / √(1-V²/c² )      –>    Δtb aumenta in questo    modo in ogni condizione?

FORSE!  LA SOLUZIONE DEL

DUBBIO_ rel1

ancora  in pdf

LORENTZ_RELATIVITA’OK1

 

CURRICULUM DI PIERO PISTOIA:

cliccare su:

piero-pistoia-curriculumok (#)

CONCETTO DI TEMPO NELLA TEORIA DELLA RELATIVITA’, del prof. Giorgio Cellai e del dott. Piero Pistoia

 

MECCANICA QUANTISTICA: appunti per una lezione; del dott. prof. Giorgio Cellai; post aperto

Testo rivisitato da il ‘Sillabario’ n. 2 1999

FONDAMENTI DELLA MECCANICA QUANTISTICA 

(del Dott. Prof Giorgio Cellai)

Da rivedere!

Parte 1°

Le parole “Meccanica Quantistica” non fanno parte dell’insieme delle nozioni indispensabili pur nell’attuale società tecnologica; acquistano significato per chi studia Chimica alle superiori, anche se è difficile andare al di là di una conoscenza superficiale; in realtà la Meccanica Quantistica costituisce il vero fondamento di quella disciplina, e questo può bene giustificare il senso di frustrazione in preda al quale si trovano (con 2/3 ore settimanali di lezione ed allievi senza le adeguate basi matematiche….) tutti i colleghi insegnanti di Chimica che conosco. Le cose migliorano, ma solo un pochino, se l’insegnante, di Fisica stavolta, riesce a ritagliare per l’argomento uno spazio consistente all’ultimo anno di Liceo; ciò è difficile, perché occorre fornire una buona conoscenza preventiva di elettromagnetismo per poter descrivere la crisi attraverso la quale è passata la Fisica prima di giungere ai risultati di cui ci vogliamo occupare.

Per una conoscenza soddisfacente sembra ormai chiaro che ci vuole l’Università, e anche un corso di Laurea a carattere scientifico sufficientemente specialistico; vorrei affrontare ugualmente l’argomento cercando di fornire, in questa prima parte del mio lavoro, delle idee generali sul significato della parola “Meccanica” e sull’evoluzione che questa ha avuto negli ultimi cento anni, culminata appunto nella Teoria Quantistica.

Alla fine del ‘600 Isaac Newton aveva definitivamente messo a punto l’impianto di una nuova meccanica che superasse quella di Aristotele risalente a parecchi secoli prima, concludendo il lavoro teorico e sperimentale di altri scienziati suoi predecessori (su tutti senz’altro il nostro genio pisano Galileo Galilei). La Meccanica è lo studio dei moti dei corpi materiali: per tale studio occorre descrivere il moto con appropriati strumenti, sia di misura (per trovare risultati numerici dall’esperienza) che matematici (per interpretare tali dati alla luce di leggi generali più semplici ed eleganti possibile). Tutti i moti su cui Newton aveva misure a disposizione furono da lui interpretati alla luce di un numero ristretto di principi: le famose tre leggi che prendono appunto il nome di Meccanica Newtoniana, o Classica, come si dice oggi. Tutti i corpi macroscopici di cui si conoscono le modalità di interazione (dai pianeti alle palle di biliardo agli zampilli di una fontana) obbediscono alle leggi di Newton; tali leggi hanno la veste matematica di relazioni tra grandezze fisiche vettoriali, cioè quantità dotate (come la posizione, la velocità, l’accelerazione) di una direzione, un verso e un valore numerico positivo o al minimo nullo che si chiama intensità o modulo. Con la seconda legge in particolare:

F = m*a             (1) 

la teoria di Newton fornisce, in funzione delle diverse possibili modalità (forze F) di interazione, l’accelerazione a del corpo in questione; dalla conoscenza di questa si può ricavare in funzione del tempo il vettore posizione del corpo, cioè predire istante per istante dove esso si trova con la cosiddetta Legge Oraria del Moto. Il calcolo della Legge Oraria si traduce nella risoluzione di quella che tecnicamente è chiamata un’equazione differenziale, quale è per l’appunto la seconda legge che fornisce una relazione tra posizione, velocità, accelerazione e tempo; il fatto è che la velocità e accelerazione sono grandezze legate alla posizione essendone le derivate (prima e seconda) rispetto alla variabile tempo. Cosa sia esattamente la derivata di una funzione è tipicamente oggetto di studio dell’ultimo anno delle superiori, nella parte dedicata all’Analisi Matematica: non mi posso addentrare nell’argomento ora, ma risulta chiaro che il problema fisico diventa un problema di calcolo e dopo Newton (che aveva fatto nel suo sforzo di fisico teorico delle scoperte fantastiche di Analisi Matematica!) molti matematici hanno lavorato a questo settore facendolo evolvere adeguatamente alla risoluzione di complicati problemi di moto, il tutto in perfetto accordo con le leggi di Newton. Tra i risultati fondamentali della Teoria delle equazioni differenziali ce ne è uno intuitivamente evidente e di grande importanza nel problema del moto: in un’equazione contenente al massimo derivate seconde rispetto alla variabile indipendente (per fissare le idee il tempo t)la soluzione, cioè la funzione che soddisfa identicamente l’equazione, esiste ed è unica se si fissano ad un dato istante t₀ il valore della funzione e della sua derivata prima. Questo è proprio il caso della seconda legge: il vettore accelerazione infatti è la derivata seconda rispetto al tempo del vettore posizione, che è la nostra funzione vettoriale incognita. Insomma, se conosco posizione e velocità ad un certo istante t₀ il moto ad ogni istante successivo è univocamente determinato; la teoria di Newton è una teoria deterministica.

I giochi ormai sembrano fatti; problemi fisici concettuali proprio non ci sono, può capitare semmai di sbattere la testa in un problema di moto con un tipo di forza complicato da trattare matematicamente. Ci penseranno i matematici, ci sono apposta: Einstein per esempio aveva il proprio “matematico personale” (pare che ne avesse cambiati diversi….). Perché allora la meccanica quantistica? Perché qualcosa cominciò a non funzionare con l’avvento della teoria atomica e con le sempre maggiori evidenze sperimentali a suo favore. Non è possibile qui dilungarsi (anche se sarebbe molto interessante!) in un’esposizione storica dei problemi che si ponevano ai fisici teorici nell’applicare le leggi di Newton ai sistemi atomici; evidentemente la Meccanica Newtoniana avrebbe dovuto funzionare anche su scala microscopica per essere veramente generale, ma vi erano difficoltà teoriche sia per conciliare di per se’ la seconda legge di Newton con le leggi dell’Elettromagnetismo (equazioni di Maxwell) che nell’applicarla anche al più semplice modello atomico (atomo di idrogeno): un nucleo (protone) carico positivamente e un elettrone carico negativamente in interazione elettromagnetica tra di loro. Il risultato drammatico era infatti che l’elettrone non avrebbe potuto orbitare intorno al protone per più di qualche centesimo di miliardesimo di secondo, essendo costretto a perdere energia irraggiando onde elettromagnetiche e a cadere sul nucleo facendo “collassare” il sistema.

Ai primi del secolo, definitivamente accertata la natura corpuscolare (atomica) della materia, Niels Bohr tentò di costruire un modello teorico dell’atomo di idrogeno (dopo quelli completamente “newtoniani” di Thomson e Rutherford) che superasse la difficoltà del collasso per irraggiamento e inoltre interpretasse correttamente il comportamento assai singolare dell’interazione tra la luce e le sostanze gassose (spettri dei gas). Ma questo modello, la cosiddetta Prima Meccanica Quantistica (1913), ammetteva ancora come valida la meccanica Newtoniana pur aggiungendovi delle ipotesi ad hoc logicamente incoerenti con essa…. era tutto fuorché una teoria elegante!

Per convincerci dell’infondatezza della teoria di Newton e anche di quella di Bohr nello spiegare il comportamento dei costituenti microscopici della materia, immaginiamo di voler fare una misura della posizione di un corpo microscopico per poterne descrivere il moto. La cosa più naturale è “fotografarlo”, cioè raccogliere attraverso un apparato sperimentale adatto alle circostanze (macchina fotografica, cinepresa, occhio …) la luce proveniente da esso nell’istante prescelto per la misura. Vogliamo fare ciò per un elettrone, un corpo microscopico estremamente abbondante in natura: lo irraggiamo con un fascio luminoso e raccogliamo con un sistema ottico (oculare) la luce diffusa dall’elettrone, deducendo da ciò la sua posizione all’istante in cui è investito dal fascio; questo vuol dire in realtà “vedere” l’elettrone. Ma è a questo punto indispensabile un’osservazione sulla natura della luce, altro capitolo affascinante della fisica: in realtà anche la luce ha una natura corpuscolare, cioè è composta da particelle elementari dette fotoni. Il nostro problema diventa lo studio dell’interazione tra il nostro elettrone e un fotone che si “urtano”: il fotone incidente viene deviato nell’urto con l’elettrone, un po’ come per due palle da biliardo, raccolto dal sistema di lenti dell’oculare e osservato (diciamo con una lastra fotografica o simile). Ovviamente però anche l’elettrone subisce una variazione del suo vettore velocità, che non può essere nulla; c’è una legge generale della Fisica che si chiama conservazione della quantità di moto e che ci può informare su tale variazione. Brevemente, la quantità di moto p è definita come il prodotto della massa m di un corpo per il suo vettore velocità: in un sistema di corpi che interagiscono solo tra loro (detto isolato) come il sistema elettrone-fotone la somma delle singole quantità di moto delle particelle è costante nel tempo, cioè non cambia anche se durante l’interazione ognuna delle p cambia. Consideriamo il nostro fotone, che viene rivelato dopo aver attraversato l’oculare: questo ha un proprio asse e un’apertura angolare  che consente di ricevere fotoni di direzione non parallela al proprio asse e di “focalizzarli” sullo schermo rivelatore. Il fotone che arriva potrebbe allora avere una componente della velocità ortogonale all’asse che noi non possiamo controllare con il nostro sistema di misura. Ciò comporta per la definizione precedente un’indeterminazione della componente ortogonale della quantità di moto che può essere stimata con le formule della Teoria della Relatività valida per i fotoni. Il suo ordine di grandezza vale:

p_x = h/ . sen  (chiamando x la direzione ortogonale all’asse dell’oculare)

Qui  è l’angolo di apertura,  la lunghezza d’onda della radiazione associata al fotone e h una costante fondamentale (detta di Planck e introdotta agli inizi del secolo con la prima Meccanica Quantistica) che vale h=6.6×10^-27 erg. sec.. Tale valore di p_x è lo stesso anche per la p_x dell’elettrone: la loro somma è infatti costante e quindi le loro indeterminazioni devono essere opposte, cioè uguali in valore assoluto, che è ciò che stiamo qui valutando.

Si può rendere arbitrariamente piccolo p_x prendendo  grande (corrispondente a fotoni molto poco energetici) e  piccolo. Nasce però un problema inatteso: da tempo i fisici sapevano che ogni sistema ottico di rivelazione, come il nostro oculare, comporta un limite intrinseco di risoluzione dovuto a un fenomeno fisico fondamentale che si chiama diffrazione della luce. Secondo la teoria della diffrazione, la luce proveniente da un punto si vede in realtà sullo schermo come una macchiolina, per cui due punti molto vicini appaiono indistinguibili sullo schermo di osservazione quando le due macchie si sovrappongono. L’ordine di grandezza dell’indeterminazione “di principio” per la posizione lungo la direzione x del nostro elettrone vale, secondo la teoria della diffrazione:

 x = /sen

 Qui, come si vede per rendere piccolo a piacere x dovremmo invece diminuire o aumentare  !….infatti si verifica facilmente, moltiplicando le due indeterminazioni, che

 p_x . x = h         (2)        (relazione di indeterminazione)

Questa è una relazione tra ordini di grandezza che è alla base della Meccanica Quantistica. La nuova teoria formulerà tale relazione in modo matematicamente più rigoroso, ma il suo significato fisico è già chiaro nella nostra versione approssimata.

Attenzione: l’ordine di grandezza del prodotto delle due indeterminazioni non è mai minore di h qualunque siano le procedure sperimentali adottate per la misura di posizione; se cerco di migliorare la precisione di p peggiora quella di x in obbedienza alla (2) e viceversa. Questo è letale per la teoria di Newton, che postulava la possibilità di misurare contemporaneamente x e v_x (e quindi p_x)! Qualcuno può pensare che questo sia solo un problema tecnico dei fisici sperimentali: nella teoria io posso “immaginare di poter misurare” x e v_x a un dato istante e poi far partire il sistema veramente bene… Nulla di più sbagliato concettualmente perché la Fisica è una scienza che si basa sul concetto operativo di misura; quando tale concetto non si può fondare oggettivamente, non si può far finta di nulla….E’ una situazione un po’ simile a quella del concetto di tempo (vd. precedenti articoli sul Paradosso dei Gemelli): era intuitivo e ragionevole pensare che il tempo t non dipendesse dal sistema di riferimento inerziale scelto, ma questo non è vero per velocità abbastanza grandi, sperimentalmente irraggiungibili ai tempi di Newton; diciamo che l’assunzione, corretta in prima approssimazione e coerente con i dati sperimentali di un tempo, si è rivelata in genere falsa. Così la relazione di indeterminazione, che la Meccanica Quantistica porrà alle sue basi, boccia la Meccanica Newtoniana, pur “elegante” e comunque funzionale per i moti dei corpi macroscopici. Ma perché allora lì funziona così bene? Perché il valore numerico piccolissimo di h rende le due indeterminazioni x e p_x inosservabili a livello di corpi macroscopici. Si pensi ad un pur piccolo pallino da caccia; posso misurarne la posizione iniziale con un apparato sperimentale molto preciso e otterrò comunque un piccolo errore strumentale “fisiologico” x; dell’indeterminazione p_x = h/x non mi accorgo assolutamente in una misura di velocità, essendo assolutamente trascurabile rispetto all’errore strumentale.

Povero Newton! Non si poteva accorgere certo né del principio di indeterminazione, né della relatività del tempo. Lo possiamo ben giustificare: ci sono voluti più di due secoli di lavoro teorico, sperimentale e di crescita tecnologica del pianeta per poter svelare questi fatti di natura.

L’esposizione finora svolta mi sembrava indispensabile per mettere a fuoco il problema; siamo a questo punto in condizioni di esporre i postulati della nuova teoria e cercherò di farlo nella seconda parte di questo lavoro.

 Parte 2°

Nella chiacchierata del numero precedente de ” Il Sillabario ” ho cercato di discutere i motivi della crisi della Meccanica Newtoniana. Questo insieme di ipotesi fisiche, tradotte in leggi matematiche semplici ed eleganti, è stato verificato sperimentalmente fin dai tempi di Newton con risultati eccellenti per quanto riguarda il comportamento dei corpi macroscopici. La sua crisi è nata con le scoperte di vari fatti sperimentali riguardanti fenomeni atomici, ai quali veniva spontaneo applicare lo schema teorico di Newton ( che chiameremo da ora ” fisica classica “), con risultati però in aperta contraddizione con l’esperienza. Le considerazioni che seguono non tengono conto dell’altro versante su cui si abbatte la crisi, cioè quello delle ” alte velocità “: in sostanza la fisica classica, oltre che essere inadeguata se applicata al moto dei corpi microscopici, lo è anche se applicata al moto dei corpi, anche eventualmente macroscopici, in moto con velocità v dell’ordine della velocità della luce c; abbiamo già trattato l’argomento alcuni numeri fa parlando di Relatività e paradosso dei gemelli. La meccanica quantistica “ordinaria” di cui cercherò di dire qualcosa ora è quella non relativistica, cioè si applica a velocità piccole rispette a c, come per esempio quelle degli elettroni negli atomi, e fornisce predizioni teoriche estremamente ben verificate nella maggior parte dei fatti di natura che cadono sotto i nostri sensi. Ricordo (vd. numeri precedenti) che l’apparato matematico della fisica classica è imperniato nel calcolo del vettore posizione r(t) di un corpo in moto nello spazio ordinario (euclideo) tridimensionale in funzione del tempo t. Lo stato di un sistema costituito da un punto materiale di massa m in eventuale interazione con altri corpi (chiamiamo punto materiale un corpo “elementare”,di cui si trascura l’eventuale stato interno, per esempio di rotazione intorno a un proprio asse) è allora completamente specificato se se ne conoscono i vettori posizione e velocità a un dato istante e le forze di interazione con l’esterno; le leggi di forza danno luogo ad equazioni che, risolte, forniscono posizione e velocità agli istanti successivi. Punto e basta. Come già discusso nel numero precedente però, posizione e velocità di un corpo non si possono misurare, e quindi definire, contemporaneamente, e quindi lo schema logico appena descritto è destituito di senso. Bisognava ripartire con principi completamente nuovi, e questo fu fatto da vari fisici teorici ( W. Heisenberg, E. Schrodinger e P.A.M. Dirac sono forse i nomi più importanti) negli anni venti dopo il primo tentativo di N. Bohr nel 1913 a cui avevo già fatto cenno nel numero precedente; proviamo ad affrontare l’argomento.

Se l’ambiente matematico della fisica classica era lo spazio vettoriale tridimensionale della geometria euclidea, quello della meccanica quantistica è ancora uno spazio vettoriale, ma di natura completamente diversa, e molto più difficile da descrivere!

A questo scopo è indispensabile dire qualcosa su cosa i matematici intendono esattamente per spazio vettoriale: è un insieme di oggetti (i vettori) su cui si definisce un’operazione di prodotto per un altro oggetto (detto scalare) che tipicamente è un numero reale o complesso, da cui si genera un nuovo vettore. Se il numero è reale l’operazione corrisponde nello spazio ordinario dei punti euclidei all’allungamento o accorciamento del vettore senza cambiarne l’orientazione, con eventuale ribaltamento rispetto al punto di riferimento se il numero è negativo. Se il numero è complesso tutto peggiora; intanto bisognerebbe dire per bene cosa è un numero complesso, e l’argomento non è banale; purtroppo nel nostro spazio vettoriale quantistico gli scalari sono proprio numeri complessi. Le conseguenze fisiche di ciò sono abbastanza rilevanti ma contentiamoci di dire che questo tipo di insieme numerico (che per esempio chi ha studiato Elettrotecnica conosce bene) contiene gli ordinari numeri reali come sottoinsieme quindi si può ancora immaginare il prodotto in molti casi come allungamento o accorciamento. L’altro fatto rilevante è che due vettori si possono sommare tra loro ottenendo un terzo vettore (nello spazio ordinario euclideo con la famosa regola del parallelogramma); la somma e il prodotto per uno scalare si possono combinare (e si parla appunto di combinazioni lineari tra vettori) ottenendo, a partire dalla scelta di un certo numero di vettori detti di base, tutti i vettori dello spazio moltiplicando ogni vettore di base per coefficienti scalari arbitrari e sommando tra loro tutti i vettori ottenuti. Ad esempio nello spazio ordinario euclideo il minimo numero di vettori combinando i quali si può ottenere un qualsiasi (cioè ogni…) vettore dello spazio è tre; così in generale si definisce una base in uno spazio e si dice che questo ha dimensione n se ha n vettori di base. Sempre nello spazio euclideo si può scegliere una terna di base (utile anche se non obbligatorio) costituita di vettori giacenti in direzioni ortogonali tra loro: si pensi agli spigoli di un cubo che fanno capo ad un dato vertice; questo dell’ortogonalità tra vettori è un altro ingrediente fondamentale della nostra ricetta e occorre per esso l’altra piccola digressione seguente. In geometria “ortogonale” ha come sinonimo la parola “perpendicolare”, è cioè collegata all’idea di coppia di direzioni “ad angolo retto”. Senza entrare nel merito sui modi di definire questo concetto in geometria elementare, è importante qui collegarlo a quello di prodotto scalare tra vettori. Quest’ultima è un’operazione che a due vettori dello spazio associa uno scalare (da cui il nome) che come già detto nel nostro spazio quantistico è un numero complesso; due vettori si diranno poi ortogonali quando il loro prodotto scalare è nullo. In fisica classica, quindi per i vari vettori tridimensionali che la popolano, (posizione, velocità, quantità di moto, accelerazione, momento angolare etc.) il prodotto scalare è un ingrediente fondamentale, nel definire per esempio il lavoro di una forza o anche il flusso di una grandezza vettoriale attraverso una superficie; in meccanica quantistica lo è forse ancora di più, essendo moltissime grandezze fisiche rilevanti della teoria riconducibili a prodotti scalari tra vettori quantistici. Ho parlato per un bel po’ di matematica; ora forse ce la facciamo a parlare un po’ di fisica come vorremmo.

Gli stati fisici di un sistema che obbedisce alla meccanica quantistica sono rappresentati dai vettori di un particolare spazio (appartenente alla categoria dei cosiddetti spazi di Hilbert), detto appunto dei vettori di stato; se due vettori rappresentano entrambi uno stato possibile per un sistema, così è per una loro arbitraria combinazione lineare a coefficienti complessi, e questo è un postulato fondamentale dalle conseguenze pesanti. Il nostro spazio ha tipicamente dimensione infinita, cioè non ci si fa ad esprimere un arbitrario vettore di stato come combinazione lineare di un numero finito di vettori di base; in molte situazioni questa circostanza non è comunque drammatica perché la base scelta della base, pur essendo questa costituita da infiniti vettori, consente comunque di lavorare con combinazioni lineari finite; esiste poi anche il modo, seppure non banale, di sommare infiniti vettori…Quello che può restare ancora, e giustamente, oscuro a chi legge è di che tipo di vettori si tratti. La risposta a questa domanda è proprio legata alla scelta della base, che, pur dipendendo dal tipo di problema, è legata agli assiomi fisici e all’apparato matematico della teoria nel modo a cui cercherò ora brevemente di accennare.

Se si misura una certa grandezza fisica in un sistema in cui vale la nostra nuova meccanica (per esempio l’energia, o la posizione, di una particella) si ottengono vari possibili risultati numerici; il fatto completamente nuovo è che ci sono dei risultati proibiti, e proibiti anche in un modo bizzarro del tutto estraneo alla fisica classica. Un esempio celebre, e già evocato nel numero precedente, è quello dell’atomo di idrogeno, costituito da un solo elettrone vincolato elettricamente da un protone carico di segno opposto a costituire un unico sistema; si può supporre immobile il protone, molto più pesante, e studiare gli stati di moto dell’elettrone nel campo elettrico generato dal protone. Ebbene, risulta che le energie dell’elettrone nei suoi stati legati (i corrispondenti delle orbite ellittiche), che sono negative in base alla scelta dell’energia potenziale universalmente accettata dai fisici, non possono avere arbitrari valori negativi come ammesso dalla fisica classica, ma un insieme discreto (quantizzato) dato dalla formula

(1)          En = -R/(n2)

con R costante (detta di Rydberg) e n arbitrario numero intero positivo, detto numero quantico principale. I valori nella (1) sono i cosiddetti livelli energetici dell’atomo di idrogeno; sono responsabili degli spettri di emissione e di assorbimento dell’idrogeno, cioè della successione di frequenze della radiazione elettromagnetica emessa o assorbita da un campione di atomi di quella specie. Questa sorta di ” carta di identità “, diversa per ogni specie atomica, è per l’appunto associata al tipo di dipendenza dell’energia, che è in generale più complicata di quella della (1) ma che è collegata comunque a ” numeri quantici “, del tipo di n, che compaiono in modo naturale nella teoria.

Per cercare di capirci qualcosa di più, accettiamo il fatto sperimentale che le energie degli elettroni degli atomi sono quantizzate e supponiamo che in generale le grandezze fisiche osservabili possano assumere valori discreti come l’energia della (1), accanto ad un eventuale insieme continuo, ad esempio tutti i possibili valori contenuti in un intervallo, limitato o illimitato. Chiameremo autovalori tali possibili risultati di una misura della grandezza fisica data; l’apparato della teoria consente di associare ad ogni grandezza fisica “seria” ( in buona parte le stesse della fisica classica più altre puramente quantistiche come ad esempio lo spin) un operatore che agisce su ogni vettore dello spazio per ottenere un nuovo vettore. Il fatto fondamentale è che con l’operatore associato ad ogni osservabile (termine quantistico che sta per grandezza fisica) possiamo calcolare di essa gli autovalori risolvendo un’equazione così costruita: se chiamo H l’operatore e  un vettore di stato, l’equazione è

H=           (2)

con  vettore opportuno e  numero reale da determinare. Il simbolo a membro sinistro è il vettore ottenuto applicando l’operatore H al vettore  . In genere  assumerà infiniti valori, discreti o continui, che sono proprio gli autovalori dell’osservabile H, mentre il vettore  associato ad ogni singolo  si chiama autovettore ( e lo stato associato autostato) di H relativo all’autovalore ; la (2) si chiama equazione agli autovalori associata all’operatore H.

Questa terminologia è stata ereditata dai matematici, che avevano da tempo costruito la teoria degli operatori lineari negli spazi vettoriali “astratti”; con l’avvento della meccanica quantistica questi sono divenuti molto più “concreti” e hanno ulteriormente arricchito di motivazioni la collaborazione tra fisici e matematici! A questo punto, a cosa servono gli autovettori di un’osservabile? Supponiamo di avere un autovalore dato, per fare un esempio il nostro  sia una delle energie E_n nella (1); supponiamo poi che _n sia un autovettore (può comunque non essere il solo…) dell’osservabile relativo all’autovalore E_n . H rappresenta nel nostro esempio l’energia dell’elettrone, inoltre la scelta della lettera H non è casuale: in meccanica quantistica, per motivi profondi su cui non posso divagare, l’operatore energia si chiama operatore hamiltoniano (o hamiltoniana) e si indica proprio con H. Un altro dei postulati della teoria è il seguente: se il nostro sistema fisico in esame è in uno stato rappresentato dal vettore , il quadrato del modulo del prodotto scalare tra  e _n ( indichiamo il prodotto scalare con (,_n) ) è proporzionale alla probabilità di ottenere, con una misura dell’osservabile H, proprio l’autovalore E_n; immediatamente dopo la misura, il sistema si porta in uno stato descritto dall’autovettore _n. Si otterrà esattamente tale probabilità ( cioè la costante di proporzionalità vale 1) se tutti i vettori di stato in gioco sono normalizzati, cioè (,)=1. Ho supposto qui implicitamente che _n sia l’unico autovettore con autovalore E_n; molto spesso ciò non avviene (si parla di autovalori degeneri) e il postulato appena enunciato andrebbe corretto, ma non mi pare il caso di complicare ancora di più le cose.

E’ d’obbligo un commento a quanto abbiamo enunciato: la meccanica quantistica è, in modo clamorosamente evidente, fondata su concetti probabilistici; essa è in grado di fornire soltanto predizioni sulla probabilità di ottenere certi risultati e non è per sua natura una teoria deterministica come quelle di Newton o Einstein; per esse le equazioni del moto conducono a predizioni non ambigue sugli stati di moto futuri per un sistema, pur di conoscere lo stato di moto ad un istante dato. Nemmeno la nuova meccanica è “ambigua”: è il modo stesso di definire uno stato che comporta indeterminazioni di principio. In alcuni casi magari la succitata probabilità vale 1 (per esempio se =_n..), cioè c’è la certezza che le misure forniscano risultati predeterminati, ma in generale il potere predittivo della teoria è di principio limitato. Il fisico non può che accettare questo dato, anche se molti (primo tra tutti proprio Einstein), pur avendo magari dato contributi fondamentali allo sviluppo della teoria, non hanno mai abbandonato l’idea di una teoria deterministica futura che superasse l’attuale.

Ora sarebbe il momento degli sviluppi di ciò che è stato enunciato: occorrerebbe molto spazio e molta pazienza, e si comincerebbe ad entrare nell’ottica del trattato, il che non rientra né negli scopi di una chiacchierata come questa nè nelle possibilità di chi la sta producendo. Non posso fare a meno di fornire ancora qualche suggestione su dove “va a parare” la teoria: avevo accennato alla convenienza di scegliere una base opportuna di vettori di stato per studiare un sistema quantistico e la scelta cade tipicamente su una base di autovettori di qualche osservabile. Se questa è l’hamiltoniana, si parla di rappresentazione di Heisenberg e per gli stati discreti i vettori sono normali vettori complessi anche se hanno infinite componenti, così come gli operatori sono matrici con infinite righe e infinite colonne… Un’altra rappresentazione, forse la più celebre, è quella di Schrodinger, in cui ad esempio per una particella si scelgono gli autovettori dell’osservabile posizione r. Tale osservabile è particolare perchè ha solo autovalori continui e il generico vettore di stato diventa una funzione complessa (r,t) detta funzione d’onda. La sua interpretazione fisica diventa la seguente: il quadrato del suo modulo ^* (l’asterisco indica il complesso coniugato) diventa la densità volumica di probabilità di misurare la posizione della particella all’istante t. Appare così un po’ più chiara quella relazione di indeterminazione trovata nel numero precedente: la posizione x di un corpo a un dato istante (riferiamoci per semplicità a una situazione unidimensionale) è una variabile aleatoria continua con una distribuzione di densità ^*; calcolandone la deviazione standard x e facendo analoghi calcoli per l’osservabile quantità di moto, definita anch’essa quantisticamente in modo opportuno in rappresentazione di Schrodinger, si ottiene la relazione esatta

          Dp.Dx >= h/4p

Ultimo dato informativo: l’equazione agli autovalori (2) per l’hamiltoniana nella rappresentazione di Schrodinger diventa un’equazione differenziale alle derivate parziali rispetto a x,y,z e t ed è la celebre equazione di Schrodinger, che, risolta, fornisce autovalori ed autovettori (chiamati qui autofunzioni)dell’osservabile energia.

Ho tralasciato in questa breve esposizione molti elementi fondamentali della teoria, come ad esempio il legame con la fisica classica, che è assolutamente non banale e di grande interesse per capire fino in fondo i principi della nuova meccanica; mi sembra però di avere fornito un numero sufficiente di elementi e mi fermo senz’altro qui, rimandando ad alcuni testi fondamentali indicati qui di seguito per eventuali approfondimenti.

DOTT. PROF. GIORGIO CELLAI 
Docente di ruolo Liceo Scientifico di Volterra

W. Heisenberg: “I principi fisici della teoria dei quanti”; ed. Boringhieri.

P.A.M. Dirac: ” Iprincipi della meccanica quantistica”; ed. Boringhieri.

M. Born: “Fisica atomica”; ed.Boringhieri.

L. Landau, E. Lifsits: “Fisica teorica 3:Meccanica quantistica”; Editori riuniti.