MEMORIA, MEMORIA…Poesie di Piero Pistoia: post rivisitato; segue commento “Un poetare che fa rivivere il passato” scritto di Andrea Pazzagli

Vedere su questo blog anche “Sperimentazione poetica; a cura di Paolo Fidanzi”

Curriculum di piero pistoia:

piero-pistoia-curriculumok (#)

PREMESSA NECESSARIA

Per capire meglio questi scritti è necessario precisare che Aquilata non è (o al tempo non era) un piccolo paese, ma solo tre case con solo due piccoli poderi e tutto il resto, macchia mediterranea spontanea ovunque si volga lo sguardo e, per avere idea della zona, sul monte Iquila, vicino a fronte neanche una casa! Dei tre bambini nominati, se ben ricordo, in piena guerra mondiale solo l’autore frequentava la scuola elementare, pluriclasse in casa privata a Massaciuccoli e poi quarta e quinta a Balbano in una scuola dello stato, gli altri lavoravano, per cui gli incontri erano rari e saltuari ed i giochi primitivi ed improvvisati, anche se, di fatto, importanti per la memoria. In quel periodo lontano per l’autore era più un giocare personale con la fantasia  fra le erbe, fra i sassi,  i filari di viti, il salire sugli alberi di leccio, la cerca di nidi…I miei ricordi, pure lontani, ma della scuola media, invece, relativi a quando ritornammo   a Pisa, bombardata dagli americani,  coperta di macerie, appena finita la  seconda guerra mondiale, i miei ricordi, dicevo, assomigliano, ma privi  però di nostalgia, a quelli riportati  nel blog  scritto dal collega Pier Francesco Bianchi  con il titolo “Brevi riflessioni sulla poesia  “memoria, memoria…”. Ma di questo secondo tempo mi rimane grande nostalgia invece per la vita nella Parrocchia  di San Marco alle Cappelle, con coetanei che ricordo ancora con amicizia e affetto (leggere “Ricordi lontani”). Forse ognuno naturalmente ha i suoi ricordi, se le esperienze sono diverse! ma per scrivere  anche un solo verso, ci vuole anima e nostalgia

1-MEMORIA MEMORIA… (con prologo ed epilogo)
2-TEMPI LONTANI DI SCUOLA
3-LA CASA D’INFANZIA

1-PROLOGO DI CARLO MOLINARO

“C’è una morte anche prima”, afferma il poeta emergente Carlo Molinaro, torinese (Lo Specchio N 135, 22-agosto-1998) e prosegue elencando alcune di queste piccole “morti”:

La distanza che si dilata
o la forza che manca per traversare.
Forse una barriera
che si chiude.
Un desiderio spento
lascia, come un falò,
una traccia sporca
sulla pioggia del greto!”

Piccole morti si nascondono anche nella nostalgia irrisolta delle poesie che seguono.

—————————————————————————

MEMORIA, MEMORIA…

Memoria, memoria …
da mezzo secolo ed oltre.
Franchino di Nortola ¹,
Giovannino ed Elsa d’Aquilata ²
(o forse Graziella?), ed io,
bimbi dei boschi.
Memoria, memoria …
della casa di roccia,
nella cima radicata ³.
Fiaschi, freschi di fonte di Rotelli ⁶,
d’acqua lontana di macchia e di macigno.
Sentieri di rupe e di fatica.
Gridi scalzi di bimbi
sulla radura di menta e nepitella.

Memoria, memoria …
La gara a salire il leccio nodoso,
la cerca dei nidi,
rincorse fra file di viti
a caccia di nuvole ed arcobaleni.
Il tasso barbasso improvviso.
Alto, lanoso, giallo splendente.

                                                                   fto di FRANCO ROSSI

Lontano d’autunno tramontana
portava branchi di colombi alla Crocetta ⁴,
e ai Ceracci ⁵ passeri in nuvole.
Spari di mio padre
e poi a casa per mano… orgoglioso.
Allora il fringuello scandiva le stagioni.

Ed … i passaggi nel cielo!

Memoria, memoria …
i bimbi dei boschi ognuno per la sua strada
e silenzio per oltre mezzo secolo.
Oggi, d’autunno
(la tramontana porta ancora colombi),
per caso passo di lì,  (7)
vecchio bimbo di quei boschi.
Sulla cima una villa,
latrati di cani (a catena?),
la strada asfaltata,
in fondo la sbarra … serrata.

I colombi hanno perso la strada.

Memoria, memoria …
memoria ritrovata,
memoria perduta … per sempre.

Piero Pistoia

¹ Nortola, scendendo verso est, piccolo podere a mezza costa fra Aquilata e Balbano (Lu)

² Aquilata, collina scoscesa coperta da boscaglie, di fronte al monte Iquila, a strapiombo sul lago di Massaciuccoli verso il mare, a ridosso del paese omonimo e con solamente tre case.

³ La “casa che la cima radica e comprende”, della poesia “TEMPI LONTANI DI SCUOLA” dello stesso autore.

⁴ Incrocio di sentieri a mezza costa.

⁵ Posto imprecisato ad est nella macchia.

⁶ Lungo il viottolo impervio che scendeva ad ovest verso Quiesa.

(7) Osservazione dallo scavalco-spartiacque Balbano-Massaciuccoli, fra Aquilata  e Iquila

EPILOGO DI CARLO MOLINARO

Ma certamente, prima o poi…,

“Porterà
a valle tutto una piena d’autunno”.

Fiume Cecina in Autunno (fto di Piero Pistoia)

——————————————————————————–

2-TEMPI LONTANI DI SCUOLA

Dal poggio isolato,
a scuola,
attraverso la macchia.
Di sasso e di spine la via.

Su rude macigno.
marucole ¹ in fiore.
Fatica di pensiero.

Stilla e spina il ricordo lontano:
paure,
preghiere,
scoscesi sentieri
nella vita e nel cuore.
Il “cervo volante” (3)
l’archètipo-insetto.

Animava l’oggetto l’attesa.

Una voce che chiama:
mia nonna.
Un affetto perduto.

Aquilata ²
si dicea quel monte
e quella casa,
che la cima radica e comprende,
ove tanto della vita persi
e tanto guadagnai. (4)

(Piero Pistoia)

¹ Marucole: si tratta di strane ginestre con lunghi e robusti aculei (Ulex europeus), alte fino a due metri, diffuse su parte del poggio di Aquilata che, dove sono,  rendono la macchia impenetrabile.

² Aquilata: vedere nota 2 della precedente poesia.

(3) Coleottero della famiglia dei Lucanidi, Lucanus cervus

(4) Guadagnai i  ‘suoni’ ed misteri della macchia e la determinazione per la sopravvivenza!

3-LA CASA D’INFANZIA

Vecchi muri (1)
spolverano
ricordi.
Nel centimetro
nascose la vita
albe remote.

Quale speranza?

Allora
vecchie e giovani
madri
curavano
i figli.
Sudava il padre
l’albero
alla macchia.

Mute grida
feriscono l’aria
di vite sofferte.

Noi,
la speranza!

Ora i muri
non lasciano pace
nel vuoto
dello spazio antico.
D’umano
calce e sasso
densi trasudano
emozioni.

Noi,
in barbara terra
estirpate radici!

Estinta la casa
stringe l’oggetto ed il cuore,
memoria si perde,
si spenge il bagliore,
singhiozzano tenui parole.

Noi,
quale fine?!

(1) Si parla della casa in Aquilata

(Piero Pistoia)

UN POETARE CHE FA RIVIVERE IL PASSATO; di Andrea Pazzagli

da continuare

Queste poesie di Piero Pistoia che evocano momenti della sua, ormai lontana, infanzia, i tempi della guerra e dello sfollamento, non sono per me nuove: ebbi infatti la fortuna di leggerle molti anni fa, poco dopo che Piero le aveva composte. Anche nomi che vi compaiono e le località che designano, in particolare Aquilata, non mi sono nuovi: ricordo che, parlando di Gerfalco, Piero fece cenno proprio ad Aquilata, località che, nel nome evocano qualcosa di arcano come gli uccelli, i loro voli, i loro nidi, difficilmente raggiungibili. Ricordo che questi versi mi colpirono particolarmente per la loro capacità di far sentire ancora vivente qualcosa di lontano, che il tempo ha cercato di strapparci, di gettare nell’oblio, ma che la parola poetica riesce come per miracolo a far risorgere quasi che tornasse quell’Allora. la medesima impressione la provo ora, anche più intensa, perché molto tempo è passato, tante cose sono successe, eppure quelle parole, quelle impressioni, vivono ancora. Ho letto qualche anno fa un libro del filosofo Rocco Ronchi (libro nel quale questo studioso cercava di delineare un percorso delle storie del pensiero diverso da quello corrente). Tra le altre cose che sosteneva vi era l’affermazione secondo cui il bambino molto piccolo prova una serie di sensazioni e di impressioni che solo in parte, divenuto adulto, ricorderà; anche quelle apparentemente dimenticate restano nel sub-inconscio ed è soltanto la parola poetica che può riportarle alla luce cancellando il muro dell’oblio che il tempo ha frattanto costruito. Come ho detto prima i versi di Piero mi colpirono e mi colpiscono profondamente. Forse perché tutti abbiamo ricordi che portano alla luce anche se poi, non siamo capaci di farlo. Ma forse anche per il linguaggio poetico di Piero che a me sembra rispecchiare quello di importanti poeti nella prima metà del novecento, poche parole tuttavia capaci di dire tante cose e toccarci nell’anima.

LETTERA SPEDITA AL CICAP, “Comitato Italiano per il controllo delle affermazioni sulle pseudo-scienze”, PER ESPRIMERE UN PENSIERO PERSONALE ALTERNATIVO; dott. Piero Pistoia, prof. di ruolo ordinario in Fisica

OLYMPUS DIGITAL CAMERA

TRACCIA DEL CURRICULUM DI PIERO PISTOIA

piero-pistoia-curriculumok-1-27Download

NDE

Per vedere l’articolo in pdf possiamo anche cliccare sotto:

cicap_lettera0

CICAP è acronimo di “Comitato Italiano per il controllo delle affermazioni sul Paranormale”. La parola “Paranormale” oggi è stata sostituita da “Pseudo-scienze”

Dopo aver letto anni fa alcuni scritti pubblicati dal CICAP decisi di esprimere alcune mie opinioni in proposito che inviai loro per posta, oggi un po’ rivisitate per precisarne alcuni passaggi [frammenti fra parentesi quadre]. Ricevetti una lunga lettera dal CICAP, scritta da un dott. prof. di Fisica Teorica di una Università del Nord, che devo ricercare in mezzo al caos della mia libreria e quando l’avrò trovata, la trascriverò volentieri in questo post.

LETTERA SPEDITA AL CICAP PER ESPRIMERE UN PERSONALE PENSIERO ALTERNATIVO, SPESSO FORZATO SU QUALCHE RAMO DI IPERBOLE, ONDE CREARE QUALCHE DUBBIO IN UN BACKGROUND DI CERTEZZE

dott. Prof. Piero Pistoia

Spett.le REDAZIONE,

leggendo la Vostra rivista si rimane colpiti dalla semplicità, chiarezza e coerente armonia – senza mai contrasti che potrebbero finire in dibattito – con cui vengono trattati e risolti i diversi problemi affrontati di cui si forniscono sempre sicure soluzioni. Sembra quasi di seguire uno dei tanti articoli di scienza pubblicato in molti giornali quotidiani e non o in una delle tante trasmissioni televisive di cultura dove tutto è descritto in maniera coerente, armonica, semplice, conchiusa e colorata [(senza un riferimento agli errori di percorso durante il travaglio (trouble) di quella conquista raccontata)], quando invece ad ogni passo del percorso si dovrebbero aprire svariati interrogativi. Se “imparare è risolvere problemi” [(e nella fattispecie, fare conti!)] da queste comunicazioni a mio avviso, pur appassionate e talora coinvolgenti, si impara ben poco. [Anzi, spesso, la chiarezza ad oltranza e l’assenza di dubbi penalizzano la memoria, la riflessione personale e quindi l’apprendimento]. Per questa ragione vorrei esprimere sulla scienza e la non-scienza o pseudo-scienza il mio personale pensiero, anche se spesso volutamente forzato lungo un ramo di iperbole, per provocare l’interlocutore e far sorgere qua e là interrogativi. Il mio intervento, di cui mi scuso in anticipo se qualcuno dovesse prendersela (absit iniuria verbis), si articolerà nei quattro seguenti punti:

1 – Se la maggior parte dell’universo è disseminato di “turbolenze”, una piccolissima variazione delle condizioni iniziali, al tempo considerata insignificante, ovvero all’interno delle soglie dell’errore, potrà provocare soluzioni impreviste ed imprevedibili con incidenza non trascurabile sul mondo fenomenico. Una esatta imprevedibilità in questi sistemi caotici (sensibili a minime differenze iniziali) presupporrebbe poter assegnare numeri reali alle misure delle grandezze che figurano nelle condizioni iniziali. Allora fattori sconosciuti di entità non misurabile, pur non potendo essere scoperte dai ricercatori, potrebbero causare grosse modifiche sui fenomeni. E ancora, onde elettromagnetiche di energia inferiore alla soglia del misurabile potrebbero produrre lo stesso effetti vistosi. Non è da escludere, infatti, che nelle condizioni iniziali, come accadeva al di sopra della soglie dell’errore, una grandezza possa acquistare due valori molto vicini, ma all’interno della soglia dell’errore potrebbe accadere che, per uno dei due, la traiettoria descritta dal sistema in un opportuno spazio delle fasi diverga esponenzialmente da un certo istante in poi, ottenendo dopo un tempo opportuno una interferenza macroscopica (o nello stesso istante ad una certa distanza?). Il mondo delle nostre misure a decimali finiti (cifre significative limitate) riguarderebbe una sezione estremamente piccola, semplice ed addomesticata dell’Universo, anche se efficace nell’ambito della sopravvivenza umana (anche troppo!), perché, come affermava Vico (Verum ipsum factum), abbiamo ‘inventato’ leggi per costruire un marchingegno che, in quelle particolari circostanze e in quei casi della realtà, estremamente ammaestrati del tempo e dello spazio, funzionasse, cioè fosse ‘vero’ per noi (e spesso accade che neppure funzioni in quelli, se ci imbattiamo in una turbolenza): si tratta di uno degli infiniti percorsi in un “reale” estremamente complesso (e forse disordinato).

Quando Galileo diceva di voler cogliere nella complessità inesprimibile dell’esperienza solo percorsi semplici, le cui grandezze fossero esprimibili con numeri a decimali limitati, voleva certamente affermare l’ambito estremamente limitato del mondo della “quantità”, unico mondo che la parte razionale della mente può capire e gestire, non essendo adatta ad affrontare l’oggetto nella sua complessità, oggetto certamente poco ordinato. E quando Galileo costruiva ed interpretava gli oroscopi (e plausibilmente ci credeva come tutti i suoi contemporanei, visto che sapeva ‘leggere’ le influenze del cielo sulla vita), voleva significare appunto l’esistenza di una parte complementare al ‘semplice’, cioè la maggior parte del mondo, che poteva venire colta in altri modi. E’ facile che Galileo non fosse un ingegnere-empirista, dedito continuamente a prove sperimentali, ma più plausibilmente un fisico teorico che quasi mai ripiegava sull’esperimento e che usava invece il teorema ed il suo “principio di continuità” come prassi scientifica usuale.

Sulla stessa linea di pensiero, per il grande logico L. Wittgenstein esiste un immenso mare tempestoso del mistico-magico che circonda, oscuro, la piccola isola del razionale, anche se poi di questo ignoto mare non se ne può parlare (è “indicibile”), usando i linguaggi della ragione (I° Wittgenstein) e degli altri “giochi linguistici” possibili (isola), nessuno è plausibile, perché non c’è realtà “la fuori” (II° Wittgenstein).

2 – I fatti, le prove, l’esperienza scientifica ‘costruita’ in laboratorio in base a precisi presupposti teorici (esperimento), non sono termini di confronto neutrali. La falsificazione (Popper) diventa impossibile non riuscendo ad individuare ciò che viene di fatto falsificato. Si perdono così i riscontri oggettivi della razionalità e sparisce il criterio di demarcazione fra sapere razionale e gli altri (arte, magia s.l., metafisica, religione…). In altre parole sono le teorie a costruire i “fatti” e a fornire le prove. Quando una teoria così diventa abbastanza organizzata tende ad auto-difendersi dall’eliminazione, prevedendo, attraverso la mente intrappolata del ricercatore (si ricordi la bottiglia di Wittgenstein), solo esperimenti favorevoli. In una iperbole, accettare una teoria scientifica invece di un’altra, nello stesso modo di accettare o no gli dèi, è solo funzione delle idiosincrasie della storia e non di qualche metodo razionale coniugato a prove empiriche. Scienza, religione, arte magia s.l., astrologia sono tutte favole che sono “vere” in senso vichiano all’interno dei loro mondi.

3 – Altri popoli e razze da sempre hanno costruito altri mondi, diversi da quello artificiale e amorale dell’uomo bianco occidentale, su altri valori, principi, credenze e uniformità e queste strutture, non necessariamente razionali (dove il magico ed il rituale giocano più che la logica e l’argomentazione critica), hanno funzionato da sempre, funzionano e, se non interverranno aliene interferenze, continueranno a funzionare (sono “vere” in senso vichiano). Quei popoli sono infatti sopravvissuti secondo i loro ritmi ed il loro senso della felicità (vivere 80 anni invece che 35, non significa un bene assoluto!). Guarda caso il progresso operato dalla scienza è misurato con i valori interni allo stesso mondo in cui si dice che la scienza opera progresso! Ci sono pregevoli culture umane, modelli di visione del mondo non derivate dalla scienza che, non solo sono capaci di far sopravvivere la specie riuscendo a controllare l’ambiente in massima armonia, ma costruiscono, a differenza della cultura occidentale, un uomo più completo all’interno, con un Io più evoluto, consapevole e vigoroso a fronte di un mera amplificazione sensoriale e percettiva sul piano simbolico, amorale nei confronti del resto dell’Universo. In ognuno di questi mondi, senza onde di probabilità né codici, avvengono “miracoli” non dissimili per quei popoli da quelli basati sulla scienza per il nostro popolo. Gli spiriti, i Mani delle cose e gli stregoni o gli sciamani che li controllano, hanno potere effettivo sugli oggetti dell’Universo anche se solo all’interno di questo cielo chiuso, come potere ebbe Afrodite sulle cose e sui cuori degli umani, quando i Greci credevano negli dèi. Nello stesso modo funziona per noi il nostro mondo artificiale, disarmonico e sovrapposto alla Natura che, divenuto meno vincolato e più potente dal succhiare continuamente la vita alle altre specie ed energia all’ambiente, spinge fino ai limiti dell’Universo conosciuto il proprio rumore assordante e la propria spazzatura. Se il nostro mondo interferisce su uno degli altri, il fragile meccanismo proprio dei mondi in armonia con la Natura si rompe, i riti si inquinano, gli spiriti si nascondono, i Mani abbandonano le cose, i miracoli cessano e la struttura culturale non funziona più; l’unica via è affidarsi allora alle mani dell’invasore, perdendo la propria identità e i propri dèi , divenendo in pratica una sottospecie. Pionieri, colonizzatori, missionari, eroi scopritori, civilizzatori, antropologi, ed altra “ciurma” di questa sorta, se ne stiano a casa loro! E’ inutile: le loro tecniche non saranno in grado di arginare i danni da esse provocati! La foresta amazzonica si salva nel segno della “empatia”, del rispetto incondizionato, com’è nei costumi “totemici” delle popolazioni indie che l’abitano e non nel segno della “scienza” e del “calcolo”, dell’uso interessato com’è nei propositi “occidentali” di finalizzarlo non solo alla sopravvivenza ad oltranza della nostra specie, ma all’aumento oltre ogni limite della sua qualità della vita! Voler giudicare e misurare con idee e strumenti del nostro mondo valori e grandezze di un altro è mera utopia, presunzione e irresponsabilità: la furba Afrodite non si farà mai scoprire dagli strumenti dell’uomo razionale!

4 – Dalle nostre parti la tradizione dominante per eccellenza è quella razionale che sostiene oggi più che mai i gruppi di potere. Dopo 50 anni di sufficiente libertà un po’ per tutti, oggi c’è la tendenza a realizzare una società fortemente ordinata e programmata dove tutto sia previsto e ogni azione vigilata e se non conforme punita. Fra poco nessuno potrà più permettersi di oscillare intorno alla norma, o, [in una metafora banale di mini-ragioneria], qualche volta calpestare un’aiola o fare una fotocopia di un articolo; [più grave superare un limite di velocità, ma sembra comunque che fra poco metteranno meccanismi registratori su qualche satellite o scatole nere all’interno delle auto; per non parlare della tendenza generalizzata ad aggiungere ad ogni carta di identità il codice DNA di ciascuno, o , magari, a misurare l’aria che ciascuno respira, perché consuma ossigeno e riempie l’atmosfera di anidride carbonica od altro gas (es. metano (sic!)… un gas serra 20 volte più potente della CO2, come afferma P. Wadhams, Univ. di Cambridge !).   Molti, seconda la strana morale occidentale, diranno scandalizzati che non si devono sostenere, per es., i primi due eventi delle aiuole e delle fotocopie (esempio metaforico, insieme ad altri, di piccole cose ragionieristiche), ma nessuno di essi potrà affermare di aver sempre rispettato il terzo evento (cose che riguardano invece la vita e la morte! Come a dire si punisce la ragioneria e si ignora la guerra! Per non parlare dei vari imposti catechismi senza un contemporaneo controllo costante sulle filiere senso lato. Naturalmente  i controllori controlleranno tutti, eccetto se stessi! Mi vengono a mente paradossi russelliani che iniziano così, per finire in contraddizioni]. L’uomo occidentale ormai disarmonico con la Natura, impaniato in migliaia di vincoli esosi, potrà percorrere ormai pochissimi sentieri ed il suo desiderio di libertà sarà fortemente frustrato. I molti sentieri infatti che non si lasciano percorrere, anche se di scarsa rilevanza, portano in nessun posto e la vita quotidiana si riempie così di una miriade di vuoti, anche se piccoli! Se a questo aggiungiamo che l’Homo sapiens sta perdendo i legami anche con i suoi simili e si sente sempre più solo in mezzo agli altri, ben vengano maghi, psicologi, cartomanti, astrologi, psichiatri, fattucchiere, preti delle diverse religioni, pranoterapisti, tecnici dell’ago puntura …, pronti a pagamento a ascoltare i problemi di vita di noi poveri diavoli. Non importa se le cose non funzionano sempre (forse perché tradizioni incomplete, parziali, aperte), ma certamente serviranno a recuperare qualche momento di pace e speranza, completamente sconosciute in questa società globalizzata del profitto e della ragioneria atomizzata, del cemento e del lungo tempo di vita. E’ giusto denunciare i profittatori (maghi, psicologi e preti…… che siano), ma pagare il giusto prezzo per i curatori di anime, mi sembra un fatto accettabile.

Concludendo, se non fosse possibile alimentare le più svariate tradizioni (scienza, arte, magia s.l., religione…) in ogni testa, sarebbe necessario farlo nella società (relativismo democratico), perché ogni tradizione porta con sé una sua visione dell’oggetto, anche se parziale, incompleta, inventata e falsa; ma l’insieme di tutti i punti di vista creerà un invariante di vita umana, un’emergenza, in particolare per l’uomo occidentale, la migliore possibile. Anche le tradizioni più squalificate e considerate negative e non degne di credibilità (es., le ‘streghe’, bruciate sul rogo a migliaia,  dal primo Medioevo alle soglie dell’Illuminismo), vanno lasciate, magari isolate in attesa, in modo che, in quel momento fuori tempo, non disturbino (J. P. Feyerabend, l’epistemologo anarchico), perché nessuno è in grado di dire quanto bene ci sia ancora nel male e in che misura l’esistenza del bene sia stata legata ai crimini più atroci (enantiodromia eraclitea); [il Bene ed il Male sono connotati dalla storia e se la Storia (Historia) è  ‘oggetto’ complesso, nessuno potrà mai prevedere quanto, per es., l’evento ‘streghe’ possa aver  ‘perturbato’ la Storia futura (in particolare le res gestae, o humanae res), nei millenni successivi, cioè nel tempo lontano. Il filosofo medioevale Tommaso d’Aquino affermava  che <<Multae utilitates impedirentur si omnia peccata districte proibentur>>.

L’oggetto della conoscenza si fa analogo ad una pozzanghera di fango, dove sono cadute alcune gemme razionali ed a intervalli si aprono e si richiudono delle bolle oscure indicibili attraverso le quali è possibile gettare un rapido sguardo nelle zone più profonde.

Ho ritenuto di non aggiungere alcuna bibliografia, sicuro che il lettore di questa missiva sarà in grado senz’altro di riconoscere dietro lo scritto i nomi degli autori a cui si fa tacito riferimento.

DISTINTI SALUTI

piero pistoia

BREVI DIVAGAZIONI SCARSAMENTE CONDIVISE SULLA NATURA E SULL’ARTE del dott. Piero Pistoia

La seguente breve riflessione in pdf:   arte_scienza-e-sassi-mammellonati

 

DIVAGAZIONI SCARSAMENTE CONDIVISE E MOLTO APPROSSIMATE SULLA NATURA E SULL’ARTE

del dott. Piero Pistoia

Il sentimento universale del dolore per la perdita di un cucciolo della stessa specie riesce ad esprimerla anche la stessa Natura giocando con il linguaggio criptato di angoli, rapporti aurei e pentagoni (così come intravisto appena dal pensiero razionale), che stranamente, per un processo co-evolutivo, anche l’animo umano riesce a tradurre in emozione!

La Natura costruisce se stessa ponendosi ad ogni passaggio davanti ad infinite scelte; le ‘annusa’, con la velocità che le è naturale (forse quella della luce)e sceglie quel cammino che consuma minore energia, si muove verso quella superficie per raggiungere la quale consuma meno energia, ecc., costruendo tutte le forme del Cosmo attraverso strutture primigenie (forse i frattali che hanno a che fare con numeri aurei, i numeri di Fibonacci, i pentagoni… o le cellular automata di Wolfram ; vedere i posts relativi). La Natura in questo modo costruisce ogni forma! Costruisce le albe ed i tramonti, le aurore boreali, le foreste, le forme delle foglie, degli animali, i densi occhi delle donne…i sassi mammellonati, insomma tutto ciò che la scienza con la matematica e la fisica sembra non riesca a spiegare fino in fondo. E di questi oggetti è pieno l’universo! Ciò che la matematica e la fisica invece riescono a razionalizzare è una porzione di spazio-tempo infinitesima rispetto al Cosmo che ci circonda, costruita nel tempo ‘lungo’ nell’interazione evolutiva con lo spazio-tempo di sopravvivenza.

E l’Arte? Proprio per la sua natura universale, svincolata dal tempo e dallo spazio, è forse costruita a partire da ‘quanti di emozione’? e l’emozione densa di energia è forse quantizzabile come la materia e l’energia, il tempo e lo spazio, ecc.? e rimanda forse anch’essa a frattali e numeri aurei o ‘automi cellulari’ come la stessa Natura? L’Arte è probabile che usi una parte del cervello umano estremamente difforme dal razionale, tale da contribuire però, attraverso un transfert-a-specifico, a quei salti creativi che nel corso dei millenni hanno compartecipato anche al progresso della scienza e della matematica.

ARTE SCIENZA SACRO ENTRANO IN INTERAZIONE SU FRONTIERE CHE SI PERDONO IN UNA FUGA INFINITA DI FRATTALI?

Dott. Piero Pistoia

VISITARE ANCHE IL POST SULLA PITTURA DI P. Fidanzi ed altri ‘MIRABILE E SORPRENDENTE MOSTRA DI PITTURA’  con foto mammellonati e riflessioni brevi su Natura ed arte, da cui è stato trasferito qui, questo mio scritto, in parte modificato.

piero pistoia

Un accademico di fisica teorica ha espresso per mail un ‘MI PIACE!’ sulla precedente riflessione.

CURRICULUM DI PIERO PISTOIA :

piero-pistoia-curriculumok (0)

SENSO DELLA POESIA E DELL’ARTE, DELL’OGGETTO FISICO E NATURALE; riflessioni argomentative aperte, ‘implicite’ e forse criptiche e quindi provocatorie: problemi dischiusi al margine; scritto del dott. Piero Pistoia

Post in divenire……

In questo scritto, nato al tempo come una relazione didattica di auto-aggiornamento oggi rivisitata, furono trascurati i riferimenti bibliografici. Da controllare, precisare ed eventualmente da aggiungere  (J. BRUNER, TORALDO di FRANCIA ed tanti altri)

OGGETTO ARTISTICO/OGGETTO REALE E OGGETTO ARTISTICO/OGGETTO FISICO 

RIFLESSIONI DIFFORMI DI PIERO PISTOIA

Perché l’argomentazione difforme e provocatoria (a differenza di quella razionale anche di buon senso, che è capace di tracciare nel complesso, per es., due percorsi razionali incompatibili, cioè A + contorno può portare a Bianco, ma anche a Nero, giustificando tutto! )  possa facilitare almeno  la consapevolezza della strana morale degli occidentali (sia quelli con grande Storia, sia quelli senza Storia, perché,  forse, Historia magistra vitae è una falsa sentenza), brava gente di cuore, di intelletto e spesso timorosa di Dio insomma, che, nel migliore dei casi, sa offrire come una grande opera morale di carità il curare feriti a migliaia e il sotterrare morti a migliaia per lo più innocenti, colpiti ed uccisi proprio da loro! Spesso con l’educare al difforme e al provocatorio si può intravedere meglio la giusta via! Chi pensate vedrà prima la stretta asola nella trappola per mosche di Wittgenstein? Il difforme o il razionale di buon senso?

PREMESSA

Accettiamo come postulato che l’oggetto poetico (artistico) e l’oggetto reale posseggano, per loro natura, ambedue infinite sfaccettature, infinite possibilità di significati razionali e/o irrazionali, ambedue non siano riducibili o coglibili fino in fondo. Gli ‘umani’ cambiano nel tempo insieme al loro background di interpretazione, ma Natura e Poesia rimangono e si pongono come un obbiettivo regolativo incompiuto….per sempre.

Postuliamo altresì che l’oggetto poetico (artistico) abbia un disordine intrinseco che si ‘attua’ in ‘vortici’ del linguaggio, come quello reale, pur nelle differenziazioni dei significati, un disordine ordinato in qualche modo, un caos con un suo ordine interno.

La comprensione dell’oggetto poetico è quindi solo parziale anche per lo stesso poeta, a differenza dell’oggetto fisico che, pur tendenzialmente in divenire, viene sempre compreso completamente ad ogni stadio, dallo scienziato che lo ‘costruisce’ (sull’oggetto fisico ci si fanno i conti, si costruiscono oggetti della tecnica e della tecnologia! Verum est factum di vichiana memoria).  L’oggetto fisico, infatti, espresso da teorie, è razionalmente comprensibile fino in fondo ad ogni fase di sviluppo a differenza dell’oggetto reale. E’ vero che possono esistere infinite possibilità fisiche di vedere razionalmente  l’oggetto reale, ma queste possibilità non saranno mai esprimibili in una teoria che abbia essa stessa infinite possibilità di interpretazione (che comunque sarebbero tutte razionali: infinità di ordine inferiore rispetto alle infinità della classe delle possibili interpretazioni dell’oggetto poetico e naturale).

L’oggetto poetico e dell’arte non è comprensibile né riducibile ad un processo razionale, né comunque esauribile da qualunque umano; la sua interpretazione non diverrà mai definitiva. Tutte le possibili interpretazioni razionali e tutte quelle emotive irrazionali o inesprimibili, coglibili solo nell’atto immediato dell’intuito, infiniti punti di vista come monadi leibniziane, sarebbero sezioni di un invariante poetico, l’oggetto poetico.

Possiamo allora concludere che l’oggetto poetico assomiglia (nel senso della complessità) di più all’oggetto reale di quanto somigli ad esso l’oggetto fisico.

Ne deriverebbe allora che l’oggetto reale, l’Alter Ego del soggetto, il noumeno kantiano, potrebbe essere compreso più in profondità se si utilizza, per la sua scoperta, l’oggetto poetico (od anche l’oggetto poetico) di quanto lo sia utilizzando l’oggetto fisico (o solo l’oggetto fisico)?

PRIMA ARGOMENTAZIONE PROVOCATORIA SUL PUNTO INTERROGATIVO NON SOSTENUTA FINO IN FONDO DALLA LOGICA  NE’ DALLA CONGERIE DI DATI SPERIMENTALI

La risposta alla domanda formulata non è possibile se non vengono precisate le condizioni di costruzione dell’oggetto poetico e in cosa consiste l’oggetto fisico. Il coinvolgimento totale del soggetto  nell’oggetto,  escluderebbe la possibilità di cogliere l’esterno del soggetto stesso, ammesso che esista. Quindi questo oggetto complesso, risultato dell’atto poetico, sembra costituire una fusione quasi mistico-religiosa, del soggetto nell’oggetto, ad animare un oggetto di per sè non coglibile, a meno che non si voglia ammettere che le cose dell’Universo consistano di una congerie di materia e spirito (Heghel). Solo in tal caso l’oggetto poetico potrebbe corrispondere all’oggetto reale in quanto costituito della stessa sostanza ed ugualmente complessi. Questi due aspetti non garantiscono però un matching necessario, in quanto può accadere che nonostante ugualmente complessi e della stessa pasta  abbiano struttura completamente diversa. E’ necessario ammettere ancora qualcosa.

Se quest’ultimo aspetto comunque fosse vero (presenza di matching), l’atto poetico sarebbe più efficace dell’atto scientifico a cogliere la realtà dell’Universo. Si verrebbe così a confermare la posizione di Vico che affermava come il noumeno potesse essere colto nell’attività mistica e artistica ed altre posizioni sostenute dalle religioni orientali.  Se poi questo aspetto non risultasse vero, allora la suddetta proposizione dovrebbe essere presa come postulato di partenza per poter sostenere il matching.

E’ comunque da precisare che, anche se l’invariate poetico corrispondesse alla realtà, ciò non significa che tale oggetto possa essere compreso completamente nell’esperienza di un solo soggetto, sia esso l’artista od il fruitore.

 

SECONDA ARGOMENTAZIONE PROVOCATORIA SUL PUNTO INTERROGATIVO NON SOSTENUTA DALLA LOGICA O DALLA CONGERIE DI DATI SPERIMENTALI

La questione potrebbe essere però risolta in un altro modo. Ammettiamo che l’Universo consista di un oggetto estremamente complesso in cambiamento evolutivo (crescita? Ontogenesi? Filogenesi?); ogni parte di esso è istante per istante in equilibrio con tutte le altre a formare un tutt’uno strutturato finemente. La stessa vita porta traccia di questa struttura nel senso che ogni parte di questo insieme porta scritto in qualche modo informazioni relative al resto dell’Universo (per es., gli elementi chimici costituenti i nostri corpi sono stati prodotti nell’esplosione di super-nove!). Pur evolvendo ogni cosa che esiste, ad un certo stadio, già c’era in precedenza, anche se in qualche altro stato. La stessa mente o spirito deve (?) essere parte integrante di tutta la materia dell’Universo. Ma il ‘deve’ nell’ultima proposizione non può essere logicamente sostenuto. Se da una scatola chiusa esce un coniglio non è logicamente inferibile che un momento prima esso fosse dentro la scatola! Si pensi ad un elettrone che esce da un nucleo radioattivo nonostante che sia impossibile per un elettrone albergare in un nucleo! Ma al  posto dell’elettrone nel nucleo c’è qualche altra cosa, per es., energia sotto forma di massa a costituire parte di un neutrone: ma è la stessa cosa? Una congerie di elementi diversi già esistenti a configurare un nuovo oggetto, è la stessa cosa dell’insieme non strutturato degli stessi elementi?

Ammettendo la validità del ‘deve’, qualsiasi atto creativo avrà a che fare con archetipi profondi legati a questa struttura dell’Universo, che, in quanto mente e corpo, è coglibile attraverso una riflessione umana. E’ possibile inoltre che l’uomo abbia formato un nodo estremamente denso di linee di struttura rispetto ad altri oggetti e quindi che i legami archetipici con l’Universo siano profondi e ricchi di informazioni.

Ma ad un certo stadio evolutivo l’equilibrio dovette cessare improvviso, come fu improvviso  (in senso geologico) il salto qualitativo che condusse l’Homo sapiens all’Homo, che chiameremo, sapiens sotto-specie sapiens (indicando il passaggio fra un Homo con corteccia in via di trasformazione, in situazione lontana dall’equilibrio,  ad uno con corteccia praticamente definitiva, come la nostra.

Non è del tutto inverosimile pensare che, data la tendenza degli svariati elementi costituenti gli organi, in particolare il cervello, a correlarsi fra loro, gli ultimi salti evolutivi, richiesti dall’uso sempre più consapevole della mano (teoria adattiva del Neo-darwinismo), abbiano trascinato nello sviluppo evolutivo una miriade di elementi cerebrali a costituire un cervello con possibilità enormi rispetto alle richieste iniziali (simile a quello che sarebbe accaduto per l’occhio estremamente complesso dei polpi). Ovvero le oscillazioni sempre più ampie intorno ad un centro lontano dall’equilibrio avrebbero condotto, in questa fase in particolare, ad un salto qualitativo non spiegabile con le richieste adattive (Teorie degli Equilibri Punteggiati).

L’inizio della mancanza di equilibrio con la Natura iniziò quando entrò in gioco la costruzione orientata ad  una attività sempre più simbolica  della corteccia e quindi l’inizio di un successivo indebolimento, in questo processo, della costruzione di archetipi legati all’azione della corteccia.

Allora, se la razionalità nella sua pienezza corrisponde a queste ultime conquiste evolutive, non è forse da chiederci se essa, certamente umana, sia davvero da considerarsi conforme alla Natura.

Si conclude: a) non ci fu più equilibrio completo da quando entrò in gioco la costruzione sempre più simbolica da parte della corteccia, aspetto del cervello non in equilibrio con la Natura; b) non si hanno archetipi legati all’azione della corteccia (?); c) l’oggetto creato dalla corteccia non è un oggetto naturale.

Così solo l’atto creativo può evocare dal profondo spinte archetipiche atte a costruire un oggetto complesso della stessa ‘pasta’ dell’Universo e ad esso corrispondente. Con l’intuizione estetica o mistica e la riflessione-meditazione filosofica profonda sembra così essere possibile raggiungere gli stessi obbiettivi della scienza ed oltre?

Si potrebbe evincere anche che l’Homo prima del sapiens, in perfetto equilibrio con l’Universo, potesse provare esperienze di fusione mistico-magico-creative con gli oggetti dell’Universo (Empatia? Einfunlung?) così profonde da poter cogliere la ‘Realtà’ in una sola esperienza personale ovvero in una esperienza condivisa all’unìsono (Telepatia?) dall’orda, esperienza catalizzata ed evocata dalla presenza dell’oggetto artistico (Neanderthal e pitture relative alla sua scultura).

MONDO DELLA MANO DESTRA, MONDO DELLA MANO SINISTRA E LORO RAGIONI

Esistono così due modi di intervento sul mondo, uno guidato da teorie e modelli logici messi alla prova usando processi razionali quantitativi di controllo o suggeriti dalle teorie del complesso e l’altro procedendo lungo le direttrici suggerite dalle teorie del qualitativo. Non si tratta però né di due aspetti ugualmente radicati profondamente come archetipi nell’animo umano, rispettivamente correlati alle filosofie della causa e del fine (razionalismo e irrazionalismo, scientismo e umanesimo, mano destra e mano sinistra…), né da cercare di armonizzare e integrare. La situazione è ben diversa: tertium non datur.

I problemi che sorgono nell’interazione uomo-natura non si risolvono, o non si procede efficacemente nella loro soluzione, muovendoci, guidati da qualche teoria della conoscenza, dalla raccolta dei dati, attraverso la loro elaborazione, per intervenire a modificare la situazione teorica iniziale, a fronte di strumenti che non permetteranno mai di cogliere la realtà di interrelazione fra le cose. La soluzione si ottiene cambiando completamente tattica e atteggiamento.

I mondi della logica, della matematica, delle scienze positive e i correlati mondi del ragionamento razionale, delle argomentazioni critiche, degli standards universali, delle prescrizioni , delle tradizioni rigide…rappresentano una sezione artificiosa e riduttiva del complesso pensiero umano. Essi derivano da una riflessione parziale ed incompleta sui processi mentali atti a rispondere  alle richieste della sopravvivenza e dell’istinto di conservazione.

Questi mondi costruiti dall’uomo che utilizzano tali processi riduttivi del pensiero,  risultano solo parzialmente umani e stranamente separati dalla Natura (mondi artificiali costruiti dall’uomo su dati incompleti relativi al funzionamento del suo pensiero e quindi scarsamente agganciati all’equilibrio naturale). Ci siamo accorti infatti non solo che a) il pensiero intuitivo-creativo non è analizzabile in termini di scansioni veloci, automatiche e non consapevoli attraverso percorsi cibernetici, l’atto creativo rappresenta una visione immediata e orizzontale della soluzione a problemi, ma anche b) tutti  gli altri  processi del pensiero umano non seguono  sempre e comunque i passi scanditi da un particolare software, atto al raggiungimento di un dato obbiettivo (non esiste necessariamente omologia fra pensiero e software).

Da questo consegue che le teorie scientifiche sono solo condizione necessarie ma non sufficienti (Toraldo di Francia) per cogliere la realtà ed il progresso della scienza si riduce solo all’adeguare funzionalmente (fitting) modelli e teorie all’ambiente sperimentato (Convenzionalismo?), nel senso della sola ricerca della semplicità, coerenza e capacità di spiegazione e previsione. Il fatto quindi che una chiave (teoria) apra una porta (risolva un problema), dalla chiave che apre non si evince niente sulle caratteristiche della porta (come da una chiave che non apre, teoria falsificata!).

Se una nave urta gli argini di un canale avvolto nella nebbia, dirò che il percorso non è adatto a descrivere la geometria del detto canale; se invece  attraversa il canale (teoria non falsificata e quindi corroborata) non posso affermare che il percorso corrisponda (match) alla traccia del canale, perché la nave può aver percorso le più svariate linee, anche fortemente a rischio, che non hanno niente  a che vedere con la “vera” forma del canale.

Il non adatto viene “falsificato” e quindi eliminato: niente però viene detto sulla “verosimiglianza” (termine di Popper), sulla corrispondenza ed omologia fra teoria ed ambiente reale (Popper è meno pessimista). Da una parte ciò conduce all’impossibilità di cogliere l’oggetto in sé , il noumeno kantiano, dall’altra alla realizzazione fattiva di opere e strutture sociali non in equilibrio né con l’uomo né con la Natura,  conseguenza delle posizioni degli efficientisti, dei manichei coerenti e intransigenti, dei possessori di verità con in tasca le chiavi dei ghetti e delle camere a gas (tutti figli del razionalismo), che, insieme ai pazzi, sono e sono stati nella storia, vicina e lontana,  i soli responsabili di efferati genocidi e di guerre inumane e  ingiuste.

Il disagio che ne deriva ha condotto alle dualità espresse nelle distinzioni già nominate fra mano sinistra e mano destra, arte e scienza positiva, mondo dei valori e mondo della ragione… e ultimamente alla individuazione di particolari problemi detti ipercomplessi, le cui soluzioni non sono possibili con i soli strumenti della ragione.

In effetti tutti i problemi che riguardano l’Universo – in particolare quelli di natura sociale – sono, a mio parere, di natura ipercomplessa, la cui soluzione è resa possibile solo attraverso una riscoperta dei profondi legami fra ragione e non, coglibili nelle primitive operazioni mosse dall’istinto di conservazione e dagli altri archetipi collegati all’ambiente di sopravvivenza (caccia e raccolta), nel quale per più di due milioni di anni il cervello ha sviluppato le proprie caratteristiche profonde. Forse nello studio del pensiero-comportamento degli ominidi fino al Neandethal, cioè prima dei Cromagnon, potremmo trovare indizi di questo aspetto mancante e abbozzare così una risposta se mai esiste.

L’inesistenza di risposte a tali dicotomie dovrebbe allora essere ricercata forse nella incompletezza del cervello umano. In tal caso comunque dovrà esistere un controllo capillare delle costruzioni artificiali, siano esse opere o ragionamenti, da parte degli aspetti umani più primitivi, ma certamente più in equilibrio col Tutto.

UNA RIFLESSIONE  FINALE: ARTE E MAGIA, SCIENZA E MAGIA

Allora con gli ultimi salti evolutivi la capacità di costruire simboli e quindi teorie fornì un nuovo metodo di programmazione e manipolazione dell’ambiente per  la sopravvivenza della specie ed oltre: un metodo certamente umano, perché posseduto dall’uomo, ma non naturale, in quanto non previsto dalle esigenze e dalla cultura (caccia e raccolta) in cui si era sviluppato il cervello umano in equilibrio col tutto.

Data l’efficienza e la soddisfazione conseguente a tali processi che facevano morire  teorie al posto di organismi, questo metodo affascinò a tal punto che fu dimenticato quasi completamente l’altro. Ed era l’altro quello in equilibrio con l’Universo, quello del rispetto dell’essere vivente, dell’oggetto inanimato e dell’energia;  quello del vivere sociale armonico e condiviso, anche se per piccoli gruppi.

Da quel momento le orde non si riunirono più intorno all’opera d’arte  (per es., una preda) a meditare al fine di cogliere l’oggetto ‘reale’, il noumeno kantiano, per controllare il futuro (procurarsi ritualmente il cibo). Da quel momento quel metodo si ridusse in brandelli, i cui resti  in tracce ancora oggi rimangono nebulosi nel profondo del nostro essere e quando riusciamo a prenderne consapevolezza si rimane invischiati in una dualità irrisolvibile. Dovevamo accorgerci da subito che l’altro, non vistoso, non luminoso ed immediato, era invece il metodo più potente, in quanto alla nostra sopravvivenza avrebbe partecipato il Tutto completamente compreso.

Molti scritti sacri delle più disparate religioni non suggeriscono forse di dimenticare la logica, la scienza e le loro opere? E le teorie, da queste discipline razionali proposte, non sono forse solo convenzioni, che funzionano sì (a guisa di protocolli applicativi), ma solo per i nostri scopi a danno di Tutto, e quindi anche di noi stessi?

Armonizzare ed integrare questi due aspetti è senza senso: con la mano destra invento costruzioni artificiali per lo più tautologiche e, forzando,  le rendo funzionali ai miei scopi (Verum ipsum factum), con la mano sinistra riesco a costruire, ormai malamente, oggetti incompleti i cui significati operativi rimangono nebulosi; le loro potenzialità, nel migliore dei casi, rimangono imprigionate al di sotto di una semplice armonia estetica virtuale che ‘accarezza l’animo umano’, come l’oggetto artistico! Pur tuttavia, un grande oggetto umano è l’arte! ma, perché incompiuto, non riuscirà mai più a gestire operativamente in maniera diretta né il presente né il futuro (forse, solo in maniera mediata dalle emozioni e dai sentimenti, sarebbe in grado di attivare comportamenti) . Oggetti sorti incompleti dalla Grande Evoluzione e gettati in un mondo di significati artificiali e innaturali: questa è la situazione a cui conduce la nostra argomentazione difforme e provocatoria

Oggi (ieri dopo il sapiens sottosp. sapiens) il processo di cogliere l’invariante poetico è solo un tentativo nella direzione dell’esperienza di fusione originale, prima degli strani mondi, dispersivi di energia, costruiti dalla corteccia. L’invariante poetico, se vogliamo portare l’argomentazione fino in fondo, potrebbe essere colto da un solo soggetto o da un piccolo gruppo, solo se esso, in profonde intuizioni meditative, fosse capace di liberarsi dalle sovrastrutture acquisite nell’ultimo o negli ultimi salti evolutivi (per es, i Santi, i mistici di qualsiasi religione e forse anche i maghi che abbiano superato i tests del CICAP e, forse, absit iniuria verbis, anche il Nazzareno era uno di quelli!).

Concludendo, l’invariante poetico sarebbe una specie di traduzione in chiave umana e naturale dell’oggetto ‘reale’, che diventa più accessibile di altre traduzioni allo sguardo della mente umana, in quanto riproposto dal profondo interno dell’uomo, dove si riflette l’Universo.

UN BREVISSIMO CONSIGLIO  PER UNA EDUCAZIONE DIFFORME

Ad un insegnamento fondato sulla ragione, che ormai purtroppo continuerà ad essere necessario per la sopravvivenza in un mondo non naturale costruito con il primo metodo descritto e che ormai non può essere distrutto o modificato (oltre 80% del terzo mondo popperiano controlla e riflette l’ambiente artificiale in cui siamo immersi ed il terzo mondo ha vita autonoma, con forte istinto di sopravvivenza!), dovremmo affiancare con estrema cura un insegnamento dove si dia spazio alla meditazione e riflessione intuitiva, utilizzando almeno la religione o la magia e l’opera d’arte: stiamo molto attenti in particolare ai nuovi metodi razionali e strutturali che vengono sempre più proposti per la ‘lettura’ dell’opera d’arte, quasi fosse un oggetto esauribile, al posto di un maggior coinvolgimento archetipico ed emotivo, profondo.

Piero Pistoia

CURRICULUM DI PIERO PISTOIA:

piero-pistoia-curriculumok (#)

BREVE RIFLESSIONE PERSONALE SU REALTA’ E SCIENZA del dott. Piero Pistoia; post aperto ad altri interventi

Per prendere visione di un breve curriculum dell’autore  andare al termine dell’articolo

realta-da-vicino-e-da-lontano in pdf; da aggiornare…non corrisponde ancora allo scritto successivo

BREVE RIFLESSIONE PERSONALE SU REALTA’ E SCIENZA 

a cura del dott. Piero Pistoia docente di ruolo di Fisica

PREMESSA

CENNI SU LEGGI SCIENTIFICHE, ALGORITMI, PROGRAMMI E ‘CELLULAR AUTOMATA’

Esempio di automa cellulareFigura  ripresa a pag. 371 del testo di riferimento “A new kind of Science”, Publischer:  Wolfram media inc. di Stephen Wolfram

• Il comportamento dei sistemi viene studiato con le leggi della scienza che forniscono opportuni algoritmi, o procedure opportune, in un programma, che gira su un computer, che è un veicolo tramite il quale gli algoritmi possono essere esplicitati ed applicati.
• Gli oggetti fisici e le strutture matematiche vengono trasformati in numeri e simboli da elaborare in un programma (scritto ad hoc), che gira in conformità con gli algoritmi.
• Il programma, nel girare, modifica quei numeri e simboli e in output otteniamo le conseguenze di quelle leggi.
• Eseguire un programma in un computer assomiglia ad effettuare un esperimento. Però gli oggetti fisici di un esperimento in laboratorio sono soggetti alle leggi di natura, mentre quelli in un esperimento al computer non lo sono; essi obbediscono alle leggi espresse nel programma, la cui forma, può essere arbitraria, purché coerente.
• In sintesi si ha così un’espansione dei confini della scienza sperimentale, consentendo di effettuare esperimenti in un universo ipotetico.
• Il successo delle leggi scientifiche tradizionali, formulate in particolari funzioni e enti matematici, spesso deriva sia dalla loro semplicità matematica, sia dal porsi come modello di aspetti essenziali di un fenomeno.
• Se invece una legge scientifica è ‘tradotta’ in un algoritmo, può acquistare forma arbitraria, purché coerente. Ne deriva che “la simulazione al computer ha reso possibile impiegare molti generi nuovi di modelli per i fenomeni naturali”; per es., un programma di calcolo di un modello chiamato “automa cellulare” ha reso possibile la formazione di un fiocco di neve. Allora molti sistemi complessi, non razionalizzabili con i metodi tradizionali della matematica, possono diventarlo in esperimenti e modelli al computer. E’ facile introdurre le leggi scientifiche la cui natura è algoritmica in un programma al computer.
• Ma anche in processi dove non esistono formule matematiche semplici che li descrivono, è possibile inserire in un programma un algoritmo che lo faccia e l’esito di tale processo può essere dedotto dal programma stesso; l’algoritmo allora verrà considerato la legge fondamentale per la descrizione del processo.
• Sorge spontanea la domanda cruciale: dividendo in due zone l’ Universo, l’una descrivibile con formule matematiche semplici e l’altra ‘costruibile’ con processi complessi, quale zona sarà predominante? 
• Le equazioni differenziali sono gli strumenti per costruire la maggior parte dei modelli tradizionali dei fenomeni naturali. In alcuni casi è possibile trovare la soluzione completa dell’equazione in termini di funzioni matematiche ordinarie (soluzione esatta), negli altri casi, che si incontrano in un’ampia gamma di discipline, , si fa ricorso a soluzioni approssimate usando metodi numerici;  in certi casi queste soluzioni si perdono in comportamenti complessi, per cui si deve fare ricorso alla matematica sperimentale. Comunque le equazioni differenziali forniscono modelli adeguati per le  proprietà globali di molti processi fisici (reazioni chimiche, passeggiate aleatorie ecc).
• Si incontrano moltissimi sistemi, in partenza con equazioni differenziali anche semplici,  le cui soluzioni si perdono in vortici e turbolenze, come appunto, per es.,  è il caso della turbolenza dei fluidi che si osserva quando l’acqua urta velocemente un ostacolo. Lo studio di questi sistemi sono riassunti in una nuova disciplina, “teoria dei sistemi complessi’, dove i percorsi si sviluppano in una successione di eventi deterministici, ma imprevedibili. Wolfram  tenta di dare soluzioni positive alle teorie della complessità per non rassegnarci all’inconoscibile con la computazione con particolari algoritmi (inventati da lui) più efficaci e vicini alla Natura di quelli della scienza tradizionale. Si pensa che esista un insieme di semplici  meccanismi matematici comuni a molti sistemi che danno origine ad un comportamento complicato (per es., la costruzione dei fiochi di neve): gli automi cellulari. “Anche un sistema di equazioni differenziali è in grado di descrivere lo sviluppo dei fiocchi di neve, ma il modello molto più semplice fornito dall’automa cellulare pare conservi l’essenza del processo con cui vengono create queste configurazioni complesse. Sembra che modelli analoghi funzionino bene anche per i sistemi biologici“, così afferma S. Wolfram nel suo articolo “Software nella Scienza e nella Matematica“, da  Le Scienze,  che ha guidato questa PREMESSA e il lettore interessato può trovare in esso chiarimenti e approfondimenti sui vari argomenti qui appena toccati; in particolare nell’ultima parte dell’articolo nominato si chiarisce e approfondisce con esempi e relative illustrazioni di computer grafica,  il significato e l’utilizzo del gruppo di algoritmi riferibili al ‘cellular automata’, in confronto con quelli della tradizione. Sempre dello stesso autore   il testo di riferimento “A new kind of Science”, Publischer:  Wolfram media inc., è consigliato per un più tecnico approfondimento. A prescindere dai nostri percorsi di conoscenza da sempre usati , allora l’Universo ‘costruisce se stesso’ come un elaboratore elettronico ‘simulando’ con specifici algoritmi? Esso ‘costruisce‘ nelle zone limitate coperte in qualche modo dalla scienza tradizionale anche la più avanzata, ma specialmente nelle altre, molto più diffuse, che resterebbero inconoscibili.
• Secondo la mia ipotesi  di interpretazione, il limite della scienza degli umani riflette la limitatezza, argomentativa e creativa, della co-evoluzione,  attiva durante la loro esistenza sulla terra (almeno per 2 milioni di anni), subita dai centri cerebrali in particolare nella grande evoluzione darwiniana; riuscire a individuare algoritmi specifici propri del ‘Cosmo nel suo complesso’ è forse un nuovo modo di vedere il mondo e quindi di fare scienza, ‘A new kind of Science’, appunto!
• Secondo il mio modesto parere rimarrebbe da precisare che cos’è che di fatto attiva ed accompagna nella sua esecuzione la ‘regola’ riassunta dagli algoritmi: è il background chimico-fisico-pulviscolare (attivazione) e la scelta di percorsi di minore energia (accompagnamento) od altro?

DA CONTINUARE…

UNA  RAPIDA RIFLESSIONE SULL’UNIVERSO: CHE COS’ E’ IL “REALE” PER I FISICI TEORICI

Da una parte, c’è, appunto,  Stephen Wolfram,  che a soli vent’anni al California Institute of Tecnology ottenne il PHD (dottorato) in Fisica Teorica, senza dare esami! presentando solo alcuni suoi lavori già pubblicati, con i suoi algoritmi trasferibili dal suo potente programma MATHEMATICA al Cosmo, che propone una nuova rivoluzione di idee attiva all’esterno della bottiglia col collo rovesciato di Wittgenstein. Sembra che la Natura non funzioni secondo matematica, geometria e fisica come affermava Galileo e tutti i fisici successivi; l’Universo non può ridursi ad astrazioni concettuali controllate dalla matematica, ma cresce (ontogenesi), evolve (filogenesi)  come un programma su un computer, che produce una successione di eventi. Wolfram scrive nel 2002 il grosso libro della sua vita (mille pagine con altrettanti outputs di computer grafica con relativi programmi scritti a partire dalla vers. quarta del MATHEMATICA), dal titolo “A new kind of Science”, Publischer:  Wolfram media inc., dove si precisa come il Cosmo nel suo complesso, compresa la vita, non è spiegabile secondo la scienza tradizionale, ma è un programma su algoritmi molto semplici che descrive e mette in atto un procedimento (es. il suo cellular automata, automa cellulare) che ‘costruisce’ foglie, alberi, nubi, le coste di isole, le forme degli animali e delle galassie… e quant’altro e non partendo da algoritmi basati su equazioni. E’ possibile individuare alcune regole semplici alla base di questo programma, ma il loro sviluppo matematico fisico di queste regole non permette di prevedere a lungo, ciò che poi è l’idea alla base della fisica della complessità (vedere i posts di questo blog relativi ai FRATTALI). In sintesi mi sembra di aver capito che Wolfram pensi di aver individuato all’interno di questo ‘programma universale’, non ancora risolvibile dal punto di vista computazionale se considerato nella sua totalità, gruppi di algoritmi che invece lo sono (per es., il suo cellular automata), che come tali (una serie ordinata di istruzioni in sequenza al di là di qualsiasi equazione matematica) un computer potrebbe elaborarli molto più velocemente di quello che farebbe la Natura, aprendo possibilità di ‘schiarire’ orizzonti futuri in anticipo, anche lontani, prima che si realizzino. Le Accademie, chiuse nella trappola di Wittgenstein, mi sembra abbiano ignorato questo evento culturale, che avrebbe potuto diventare forse anche grande (molti fisici teorici, almeno in Italia, neppure sanno chi è Wolfram  e inoltre non mi risulta che  il suo libro sia stato tradotto in italiano!), proprio come accadde a Galileo con la sua  Natura ‘risolvibile’ in geometria, rischiando il rogo (interpretazione tout-court). Un modo di screditare l’evento mi sembra sia stato anche quello di averlo paragonato alla ‘formula universale per tutte le scoperte’ che propose Moebius, il fisico teorico della commedia grottesca ‘I FISICI’ scritta nel 1961 e rivisitata nel 1981, il cui contenuto ruotava intorno ad un manicomio. DA PRECISARE E…..CONTINUARE

Dall’altra, c’è il mondo dei fisici teorici che cerca di guardare il ‘reale’ da due importanti punti di vista:

• l’uno che cerca di razionalizzare il Tutto, il Caos, il mondo dei Frattali, tanto da ridefinirlo Caos Deterministico (Ilya Prigogine Nobel nel 1977) nel senso che sembra controllabile da equazioni anche se non lineari, le cui soluzioni lasciano però zone d’ombra piene di vortici, rimanendo così poco efficiente nelle previsioni del futuro, come già accennato;
• l’altro punto di vista rivolge l’attenzione ai ‘mattoni’ che compongono la struttura portante del Cosmo, cioè le particelle elementari in espansione (ciascuna con una propria onda analoga a quella di Shroredinger) oggi controllabili anche dalle equazioni della Meccanica Quantistica Relativistica, riempiendo l’Universo di un ‘groviglio collettivo ‘(ENTANGLEMENT) di infiniti ‘oggetti quantistici’ interdipendenti che trovano la loro consistenza in una miriade di onde di probabilità in interazione che variano, in ogni punto, nel tempo e, ad ogni istante, nello spazio. Questo oceano in tempesta di onde di probabilità sarebbe la ‘realtà’ nel senso che, viste da lontano, (come le percepiscono l’uomo e gli animali) apparirebbero come nubi, boschi, animali, compreso l’uomo,oppure stelle o pianeti o tramonti o soli ….o il grosso leccio annoso che vedo dalla finestra o le erbacce, per es., la bonariensis (vedere i posts su un percorso floristico in questo blog), lungo un percorso di periferia (realtà apparente); mentre da vicino (lette attraverso il modello matematico offerto dalla Meccanica Quantistica Relativistica) riacquistano la loro essenza primigenia (la realtà vera) di oceano tempestoso di onde di probabilità interagenti comprensibile solo attraverso sistemi di equazioni matematiche della MQR.

Per chiarire questo ambiguo e duplice modo di guardare all’Universo proposto dalla fisica teorica alla ricerca della sua primigenia struttura, troviamo, nel quadro impressionista con le sue pennellate di colore individuali, un esempio analogico, ripreso come concetto dal testo “Il Bosone di Higgs”, RBA, 2015. Da qualche metro di distanza la pittura appare con le macchie di colore che sfumano costruendo la figura riportata nel quadro. Però se ci avviciniamo, la figura sembra scomparire e più guardiamo da vicino, percepiamo sempre più le macchie colorate separate. Se poi, immaginando anche che più ci si avvicina più le macchie fluttuino modificando colore e posizione (per cui in ogni punto si potrebbe trovare un qualsiasi colore, anche se con più probabilità quello corrispondente al disegno), ci si perderebbe in un caos di colori. Concludendo, anche se è vero che in un punto può apparirci anche ora un bianco ora un nero e così via, in effetti a circa qualche metro rivedo la pittura originale. Che cosa è più vero l’insieme delle macchie di colore separate o la pittura? Che cos’è allora la Realtà? Quella che vedono e con la quale interagiscono gli animali o quella che ‘vede’ il sistema di equazioni della MQR? E le emozioni, i sentimenti … che, densi, anche loro veicolano energia?

Prima della scoperta del Bosone di Higgs le particelle elementari non avevano ancora una massa? 

Leggere e confrontare anche  il post provocatorio dello stesso autore “La teoria e la realtà”.

CHI E’ L’AUTORE (traccia): Curriculum di Piero Pistoia

piero-pistoia-curriculumok (#)

ORIGINE DIFFICILE E TORMENTATA DELLE GEOMETRIE NON EUCLIDEE; una scaletta di appunti brevi per una ricerca scolastica; del dott. Piero Pistoia

POST IN VIA DI COSTRUZIONE: le versioni intermedie possono contenere bugs e imprecisioni!

Leggere su questo blog anche  il post sulle geometrie non euclidee (GEOMETRIA E NATURA) di cui questo intervento potrebbe porsi come premessa

LA NASCITA DIFFICILE E TORMENTATA DELLE GEOMETRIE NON EUCLIDEE

Una breve scaletta di appunti per una ricerca scolastica

A cura del dott. Piero Pistoia

 Al termine dell’articolo si può prendere visione di un breve curriculum di P. Pistoia

Per rileggere di più su  definizioni e dimostrazioni, sfogliare un qualsiasi testo per la Scuola Media (es., Fortini-Cateni, per la Scuola Superiore).

Per le argomentazioni sul V° postulato seguiremo le linee suggerite  dal testo di Mario G. Galli  dell’università di Firenze “Spazio e tempo nella scienza moderna Parte  I”, Ed. Cremonese

I disegnetti per le dimostrazioni sono stati ripresi dai precedenti testi e di questo ringraziamo gli autori

Due furono le convinzioni ereditate dalla Storia nel corso numerosi secoli, che ostacolarono e ritardarono la nascita delle Geometrie non Euclidee.

1 – Le convinzioni ereditate dal mondo greco, radicate nel corso di svariati  secoli, che assumevano le affermazioni della geometria come ‘vere’ (raccontavano il mondo), opinione garantita dall’intuizione.

2 – La sistemazione di queste concezioni intuitive della geometria, con la formulazione dei Giudizi Sintetici a priori*, nel sistema filosofico kantiano, con la pubblicazione della sua ‘Critica della ragione pura’. Cioè tutte le affermazioni della geometria venivano sostenute definitivamente da facoltà mentali a priori e la verità della connessione mente-mondo esterno non aveva bisogno di conferme sperimentali e quindi era indipendente dall’esperienza e dall’esperimento sul mondo, pur fornendo informazioni ‘vere’ su esso (sintetiche). Forse la mente organizzava i dati sul mondo (le sensazioni) nel modo in cui riusciva a farlo, perché era costruita in quel  modo acquisito nel processo co-evolutivo col mondo stesso anche se in ambiti spazio temporali limitati. Egli così giudicava la geometria come scienza assoluta della struttura dello spazio fisico.

Al tempo di Kant quindi l’interesse dei geometri non era quello di pensare a geometrie alternative per il mondo, intrappolati come erano in una bottiglia di Wittgenstein con il collo ripiegato con asola molto stretta (leggere l’art. relativo alla TRAPPOLA PER MOSCHE in questo blog)!

Nella geometria di Euclide, quella di cui si parla, esiste un postulato che già allora destava sospetto, il V° postulato del suo sistema geometrico che può essere così espresso: da un punto non appartenente ad una retta si può condurre una ed una sola parallela alla retta data. Per questo postulato, parlando della parallela condotta da un punto ad una retta data, si dovrà dire la parallela e non una parallela.

_______________________________

UN INTERMEZZO DI BREVE RETROSPETTIVA – Già era stato dimostrato il teorema che per un punto esterno ad una retta era possibile tracciare una ed una sola perpendicolare alla retta data (che poteva utilizzare il precedente teorema sulla esistenza ed unicità della bisettrice) e, come conseguenza, il teorema che, per un punto esterno ad una retta si può condurre una seconda retta non avente alcun punto in comune con la prima, ottenendo così due rette sullo stesso piano non aventi punti in comune dette rette parallele (definizione). Da questa definizione, ne deriva una nuova formulazione del teorema precedente, che per un punto dato è possibile condurre una parallela ad una retta data. Di conseguenza, come era accaduto per la perpendicolare,  se esiste una retta parallela ad una data, nasce la domanda se questa sarà unica. Se non riusciamo a ‘costruire’ quest’ultimo teorema (unicità della parallela) dal lato puramente razionale è arbitrario l’ammettere o no tale unicità  (per un punto fuori da un retta sarebbe cioè possibile tracciare una, più di una o nessuna retta parallela alla retta data!). Nella geometria euclidea, non potendo dimostrare questo, fu introdotto sotto forma di postulato, appunto il V°!

________________________________

Infatti già Euclide, chiaramente indipendentemente dai kantiani, sembrò essere molto perplesso sul suo V° postulato**, se aspettò a dimostrare almeno trenta teoremi indipendentemente da esso, prima di introdurlo.

D’altra parte anche ai geometri al tempo di Kant sembrò avessero dei dubbi; infatti  ritenevano il V° sì necessario ed evidente, ma molto più complesso degli altri. Infatti i geometri in generale, pur ammettendo che tutti i postulati proposti erano di per sé evidenti, non lo erano tutti nello stesso modo. Si posero il problema se il V° potesse essere indipendente dagli altri. Bastava controllare come ipotesi, se usando gli altri (postulati o teoremi da essi dedotti), si potesse impostare un teorema che avesse come tesi il V° postulato.

Se fossero riusciti ad articolare questa dimostrazione, che cosa avrebbero ottenuto? Non avendo altre perplessità su altri postulati, forse il tempo per proporre geometrie alternative si sarebbe molto allungato, o forse la nuova geometria ottenuta avrebbe ‘matchato’  (part. pass. italianizzato da matching ***, alternativo di fitting), il mondo (geometria assoluta)!!! Lo stesso Bolyai nel 1832  chiamò assoluta la geometria dedotta usando tutti i postulati di Euclide eccetto il V° (una trentina di teoremi). Ma oggi sembra che il valore attribuito in generale a tutti i postulati non sia diverso da quello attribuibile al V°.

Quando è possibile allora sostituire il V° postulato con uno completamente diverso?

risp.1: quando il V° postulato risultasse non derivabile dagli altri, cioè fosse dagli altri indipendente!

risp.2: qualora la geometria non fosse una scienza

Al tempo ci furono tentativi svariati di dimostrare questo tormentato teorema indipendentemente da varie parti e su vari fronti. Teoremi tutti coerenti e tutti sembravano ‘colpissero’ in maniera precisa la tesi, ma…****

Tutte queste argomentazioni critiche stavano contribuendo a costruire un aspetto del Terzo Mondo di Popper e già si abbozzavano  alla sua frontiera gli incastri che soddisfatti avrebbero precisato le idee delle nuove geometrie: il tempo della loro origine si avvicinava.

DI QUESTI TENTATIVI NE FAREMO ESEMPI NEL PROSIEGUO

GEOMETRIA EUCLIDEA E NON 10

Cliccando sopra otteniamo lo scritto successivo  rivisitato (vers. 10) in pdf, in ordine migliore  e in parte corretto, anche se non definitivo.

_______________________________________________________________________

DA CONTINUARE……

ALCUNI TEOREMI DI RETROSPETTIVA DI GEOMETRIA EUCLIDEA PIANA

Disegnetti da Fortini-Cateni

Definizione di bisettrice di un angolo: la bisettrice è la semiretta che divide l’angolo al vertice in due angoli uguali

Si dimostra che, per qualsiasi angolo (convesso, concavo, piatto), la bisettrice esiste ed è una sola.

Accenniamo al caso dell’angolo convesso. Sui lati prendiamo dal vertice A due segmenti uguali (AD=AE) e congiungiamoli. Prendiamo un punto F all’interno dell’angolo e congiungiamolo a D e a E. Se l’angolo FDE è diverso da FED, per es., minore, da E  tracciamo la semiretta EH che forma un angolo DEH=EDF e incontra DF nel punto G (postulato). Il triangolo il triangolo DEG è isoscele. Si considerino i due triangoli ADG e AEG che sono uguali per il III° criterio di uguaglianza dei triangoli. Ne deriva che la retta AG è la bisettrice. Essa è unica perché ogni altra divide l’angolo al vertice in pari disuguali.

Consideriamo ora la bisettrice dall’angolo piatto. si prenda un punto D all’interno dell’angolo e lo si unisca con A; se l’angolo BAD e CAD risultano uguali, la semiretta AD è la richiesta; se invece sono disuguali, sulla maggiore costruiamo la semiretta AE in modo che l’angolo BAE sia uguale all’angolo CAD; otteniamo un angolo EAD che è convesso; cioè esiste una semiretta AF che lo divide in parti uguali.

Semiretta che biseca un convesso un angolo piatto un angolo concavo

Unicità della bisettrice nel caso dell’angolo convesso BAC. Ogni altra semiretta AH diversa da AG, lo divide in parti disuguali. Infatti dalla figura abbiamo BAH>BAG=GAC>HAC a maggior ragione BAH>HAC. IL ragionamento è analogo per gli altri due angoli c.v.d.

Se l’angolo BAC è concavo, sia AE la semiretta che dimezza l’angolo convesso che ha gli stessi lati. Si tracci la semiretta AF opposta ad AE che divide l’angolo concavo BAC in due parti uguali. Infatti gli angoli FAB E FAC risultano uguali perché supplementari (la loro somma è un angolo piatto) dei due angoli uguali BAE e CAE.

_________________________________________

Definizione di perpendicolare: la perpendicolare da un punto esterno P ad una retta è la semiretta da P che fa due angoli uguali sulla retta, cioè due retti; la perpendicolare tracciata da un punto O qualsiasi della retta, è la semiretta che parte da O e costruisce due angoli retti sulla retta.

Come conseguenza, nel caso di una perpendicolare da un punto C (vedere sotto) fuori di una retta condotto alla retta è esistente ed unica. Facendo ruotare il semipiano di C intorno alla retta e tornando indietro, ottengo l’immagine del punto C, cioè D nell’altro semipiano. Si colleghi C e D ottenendo il punto di intersezione sulla retta, O. Vogliamo dimostrare che la retta CD forma con la retta AB angoli uguali. Ripetendo la rotazione la semiretta OC si sovrappone alla OD e l’angolo BOC si sovrappone all’angolo BOD e quindi sono uguali e la retta CD e perpendicolare a AB.

La perpendicolare è unica perché, tracciando CF, si forma il triangolo COE di cui l’angolo CEB è esterno maggiore di ogni angolo interno non adiacente (anche del retto).

Dimostriamo ora l’esistenza e l’unicità del punto medio di un segmento.

Dalle due figure sopra, dimostrato dalla prima che in un triangolo isoscele la bisettrice dell’angolo al vertice è perpendicolare alla base e la divide per metà, consideriamo nella seconda il segmento AB e un punto C, e colleghiamolo con A e B. Se l’angolo CAB è diverso dall’angolo ABC per es., minore, sul maggiore tracciamo una semiretta BD che faccia un angolo uguale a CAB e incontri AC nel punto E. Colleghiamo E con F. All’interno di un angolo, qualsiasi retta dal vertice attraversa sempre i segmenti che collegano qualsiasi coppia di punti presa sui lati (postulato). Si ha così un triangolo isoscele con gli angoli alla base uguali (lati obliqui uguali). Tracciamo la bisettrice dell’angolo al vertice AEB che per il teorema precedente è anche altezza e divide la base in due segmenti uguali. Il punto F è il punto medio del segmento AB. Esso è unico perché per un qualsiasi altro punto G,

AG>AF=FB>FG, a maggior ragione

AG>GB

_________________________________________________

I disegnetti successivi sono ripresi da M. Galli

• Definizione di rette parallele: due rette sono parallele se, comunque  prolungate non si incontrano mai.Usando il teorema precedente (esistenza ed unicità della perpendicolare) si dimostra il teorema che da un punto esterno ad una retta è tracciabile sempre una parallela alla retta data.I teoremi descritti fino qui non utilizzavano il V° postulato, come anche i criteri di uguaglianza dei triangoli e l’esistenza ed unicità del punto medio di un segmento ed altriL’unicità della parallela per il punto esterno, invece, fa parte del V° postulato così enunciabile: data una retta e dato un punto P fuori di essa, per il punto P passa una parallela (teorema) ed una sola (cuore del postulato).Con il V° postulato si può dimostrare il famoso teorema della somma degli angoli di un qualsiasi triangolo che afferma che tale somma è pari a 180° (un piatto o due retti). Ciò significa che il teorema della somma degli angoli interni di un triangolo ‘contiene’ il V° postulato, nel senso che presuppone la validità dell’unica parallela.Senza il V° postulato possiamo dimostrare solo che la somma di due angoli qualsiasi di un triangolo e minore di due retti, cioè di un piatto o 108°e, nel contesto di questo teorema, si dimostra anche che ogni angolo esterno di un triangolo è maggiore di ciascuno degli angoli interni non adiacenti o uguale alla somma dei due angoli interni non adiacenti. Vedere dopo anche la dimostrazione più articolata di Legendre.

Teoremi dell’angolo esterno di un triangolo

Dato il triangolo ABC si prolunghi il segmento AB e tracciamo una semiretta da A passante per il punto medio M, che è esistente ed unico (vedere il teorema già dimostrto), del segmento BC. La semiretta da A a D, interna all’angolo CAB incontrerà certamente (postulato) il segmento CD che collega una coppia di punti sui due rami dell’angolo. Su tale semiretta prendiamo un punto D tale che AM=MD. I due triangoli AMC e BMD sono uguali per il primo criterio di uguaglianza dei triangoli perché hanno uguali gli angoli AMC e BMD perché opposti al vertice e il lati CM e AM del primo triangolo sono uguali rispettivamente a a MB e MD del secondo per costruzione. Ma in triangoli uguali a lati uguali si oppongono angoli uguali, per cui sono uguali gli angoli ACM E MBD (gamma). D’altra parte  la somma degli angoli beta (β) e gamma (γ) sono minori di due retti, in quanto γ è interno all’angolo esterno, c.v.d.; d’altra parte dalla figura l’angolo esterno (di lati BC e prolungamento di AB) è maggiore di γ che ne è una parte, per cui è maggiore dell’angolo interno non adiacente, c.v.d. La dimostrazione può essere ripetuta su ogni lato. Manca la relazione fra l’angolo esterno e la somma degli interni non adiacenti.

Con il teorema appena dimostrato che la somma di due angoli interni di un triangolo è minore di due retti, dimostriamo la prima parte del postulato V°, cioè l’esistenza di una parallela alla retta data per un suo punto esterno.

TEOREMI SULLA PARALLELA

Da P conduciamo la perpendicolare alla retta r; sia questa PQ. Conduciamo per P la retta s perpendicolare  a PQ. Ne   consegue che gli angoli alfa (α) e beta (β) sono uguali e retti. Se la retta r incontrasse la retta s, le due rette con PQ formerebbero un triangolo con  la somma degli angoli superiore a 2 retti. Questo è assurdo per il teorema precedente. Si conclude che le due rette sono parallele, per cui esiste una retta parallela (la s) alla retta r passante per P.

Ma questa parallela è unica? Ora se consideriamo un’altra retta k passante per P e distinta da r, siamo sicuri che questa incontri ad un certo punto r? Euclide ipotizza che si incontrino dalla parte del piano dove la somma degli angoli corrispondenti è minore di 2 retti. Questo è il cuore del quinto postulato intuitivo, ma forse più complesso degli altri. Il fatto che due rette prolungate non si incontrano mai (rette parallele),   significa che sono anche equidistanti? Nel tempo fu proposto di definire una parallela ad un’altra come la retta da essa equidistante. La proposizione ‘il luogo dei punti equidistanti da una retta data appartengono ad un’altra retta  parallela alla prima’,  è sostenuto dalla nostra intuizione, ma non è derivabile  dagli altri postulati, come l’unicità della retta parallela per un punto esterno; in questa proposizione è contenuto già il V° postulato. Quindi si tratta di un postulato analogo al V°. Se sostituissimo al  quinto  la detta definizione potremmo dimostrare con altri postulati e teoremi che la retta passante per P e non intersecante l’altra, è unica, cioè il quinto postulato!

Gli antichi matematici, come già accennato, tentarono di dimostrare questo strano postulato (croce e scandalo della geometria elementare, come ebbe a dire D’Alambert), ma i loro tentativi non sortirono altro effetto che quello di sostituire al postulato di Euclide altri postulati del tutto equivalenti. Le affermazioni di partenza di questi matematici nascondevano un postulato analogo a quella da dimostrare!

Così, volendo eliminare  il V° postulato, iniziando l’argomentazione con il teorema degli angoli interni del triangolo dimostrato anche con il V° di Euclide, potremmo raggiungere deduttivamente anche l’unicità della retta parallela. Dovremmo però sostituire tale teorema come postulato del sistema al posto del V°. L’obbiettivo di dimostrare il V° eliminandolo falliva, anche perché  il nuovo postulato era meno intuibile del vecchio. Si potrebbe a questo punto continuare a tentare di dimostrare il teorema degli angoli interni di un triangolo escludendo il V°, indirettamente trasformando il V° in teorema, ma tutti i tentativi fallirono.

 

PREMESSA L’EQUIDISTANZA DI DUE RETTE, L’ UNICITA’ DELLA PARALLELA SEGUE LOGICAMENTE

Il postulato dell’unicità della retta per il quale non è possibile proporre una logica spiegazione, in effetti contiene le seguenti proposizione

1 – L’intuizione suggerisce che posano esistere due rette equidistanti, cioè che il luogo dei punti equidistanti da una retta debba essere un’altra retta.

2 – Se due rette si incontrano in un punto O, è intuibile che presi due punti equidistanti da O, OP = OQ, se la distanza OP cresce oltre ogni limite anche il segmento PQ cresce oltre ogni limite.

Ammesso questo come postulato dell’equidistanza, è possibile dimostrare che una retta non equidistante debba incontrare l’altra, cioè l’unicità della retta che diventa un teorema!

Si dimostra col V° postulato che OP e PQ sono direttamente proporzionali. Senza il V°, Euclide dimostrò che se OP supera ogni limite lo fa anche PQ e dimostrò che una spezzata condotta fra due punti è più lunga del segmento di retta che li unisce eche in un triangolo rettangolo l’ipotenusa è più lunga di ogni cateto. Cos in un triangolo rettangolo ‘coperto’ da una successione di angoli come quello sopra, di ha: OA < n*AB e AB > OA/n se il segmento OA tende all’infinito lo fa anche AB.

Dalla figura, tenendo conto delle argomentazioni precedenti risulta che spostando M oltre ogni limite anche il segmento MK fa altrettanto; infatti raddoppiando la figura coll’angolo OKN, spostando M verso l’infinito, analogamente si comporta il segmento MN come già dimostrato; per cui anche il segmento MK, cioè la distanza dalla retta OB, la metà di MN, fa altrettanto.

Ne consegue il seguente teorema conclusivo:

Siano r ed s due rette equidistanti (fig. sopra) e sia delta la loro distanza. Si consideri un’altra retta k che formi con r un angolo alfa piccolo a piacere. Procedendo lungo questa retta la distanza PM deve crescere oltre ogni limite, uscendo uscendo ad un certo punto dalla striscia compresa fra le due rette, incontrando la retta s, di qui l’unicità della parallela.

PREMESSA LA SOMMA DEGLI ANGOLI DI UN TRIANGOLO UGUALE A DUE RETTI, SI PUO’ DIMOSTRARE L’UNICITA’ DELLA PARALLELA

Qui va il disegno di una retta orizzontale con due perpendicolari verticali in A e B

Si abbia una retta orizzontale v che passa per i punti A e B; da essi tracciamo verso l’alto due rette r ed r’ perpendicolari a v. Si deve dimostrare che r ed r’ siano equidistanti (AB=PQ), in quanto abbiamo dimostrato prima, che equidistanza implica unicità.

I due triangoli APQ e ABQ sono uguali perché hanno due lati uguali e l’angolo compreso (alfa=alfa1), per il primo criterio di uguaglianza. Alfa è uguale da alfa1 in quanto alfa1+beta1 =90° e anche alfa+beta1=90° per cui alfa ed alfa1 sono complementari dello stesso angolo beta1. Alfa1+beta1 sono un retto perché k1= un retto e la somma di alfa1+beta1+k1 (somma angoli di un triangolo, ipotesi iniziale) = 2 retti. Ne deriva l’uguaglianza di AB=PQ e, poiché la coppia PQ è arbitraria, le due rette r e r1 sono equidistanti e per il teorema già dimostrato ne consegue l’unicità della parallela. c.v.d.

Possiamo ottenere lo stesso risultato in un modo diverso. E’ necessario introdurre prima un lemma.

Definizione di Lemma: proposizione importante per la dimostrazione di un teorema successivo.

Ammesso come postulato il teorema della somma degli angoli interni di un triangolo, è possibile come primo passo costruire un triangolo rettangolo con uno degli angoli acuti minore di una quantità piccola piacere (lemma)

Dalla figura sotto siamo partiti da costruire un triangolo retto e isoscele BAC, sia omega uno degli angoli acuti uguali.  Prolunghiamo AC e sulla prolunga segnamo un punto C1 tale CC1 sia uguale a BC. Si ha il triangolo isoscele in cui CC1B=CBC1 . I due angoli sono gli interni non adiacenti dell’angolo esterno ACB. Sapendo che l’angolo esterno di un triangolo è uguale alla somma dei due interni non adiacenti si ha che l’angolo esterno al triangolo BCC1 è uguale alla somma degli angoli CC1B+CBC1; se chiamiamo il valore comune dei due angoli non adiacenti ω1, ω=2*ω1 e ω1=ω/2. Possiamo continuare la costruzione prendendo sul prolungamento di AC il punto c2 tale C1C2=BC1; ne risulta un nuovo triangolo isoscele BC1C2 con angolo esterno ω/2 e angoli interni non adiacenti ω/4 e cosi via. Se facciamo n costruzioni come le precedenti si giunge ad un triangolo rettangolo dove l’angolo sul prolungamento  sarà ω/2^n. Se n diventa sempre più grande avremo un triangolo rettangolo con uno degli angoli acuti piccolo a piacere. c.v.d.

Con il risultato del teorema precedente sarà facile dimostrare l’unicità della parallela.

 

Dimostriamo il teorema che, se la somma degli angoli interni di un triangolo è due retti (postulato di partenza), allora  è ‘vera’ l’unicità della parallela, che cessa di essere a sua volta un postulato.

Consideriamo un punto P fuori della retta r. tracciamo da P la perpendicolare ad r incontrata in Q; conduciamo poi per P la retta s  perpendicolare a PQ. Ipotizziamo che la retta s non possa incontrare la retta r. Conduciamo ora attraverso P un’altra retta non coincidente con s ed ammettiamo che formi con PQ un angolo inferiore ad un retto, il cui complementare (che è l’angolo che sommato al precedente dà un retto) lo chiameremo lambda (λ). Costruiamo il triangolo QMP di cateti PQ e QM. Come abbiamo visto nel precedente lemma, QM potrebbe essere così lungo che l’angolo QMP possa divenire più piccolo di una quantità qualsiasi assegnata, anche minore di λ. Ammesso che la somma degli angoli di un triangolo sia due retti, l’angolo che la retta PM forma con s deve divenire minore di λ. Allora la retta K, interna all’angolo QPM, incontrando PM la r, a maggior ragione incontrerà anch’essa r. Così ammettendo come postulato il teorema della somma degli angoli di un triangolo, ammettiamo anche il postulato di Euclide (V°) con tutte le conseguenze. Così la geometria elementare, anche quella studiata nella scuola media, rimarrebbe immutata nella sostanza.  Ma il teorema degli angoli del triangolo è certamente meno intuitivo del V° postulato, anche se forse più controllabile con con un esperimento, considerando l’affermazione come un goal regolativo; difficile sarebbe invece controllare sperimentalmente cosa fa una ‘parallela’ molto lontano!)  DA CONTROLLARE….

PROPRIETA’ RELATIVE ALLA SOMMA DEGLI ANGOLI DI UN TRIANGOLO; USANDO I POSTULATI EUCLIDEI SENZA IL V°

La dimostrazione è dovuta a Legendre, riportata da Galli,  che “In nessun triangolo la somma dei suoi angoli interni non può mai superare due retti”. Come conseguenza si apriranno così le due possibilità che ; 1) sia uguale a due retti; 2) sia minore di due retti.

Consideriamo la figura sotto analoga a quella precedente per dimostrare i teoremi dell’angolo esterno di un triangolo. Sia ABC il triangolo primitivo; si prolunghi il lato BC in CD; sia M il punto medio del segmento BC (che esiste ed è uno solo); si unisca A con M e sul suo prolungamento si prenda il segmento MC’=AM; si tracci la semiretta di origine B e passante per C’;essa cade necessariamente all’interno dell’angolo CBD dove BD è il prolungamento di AB. Confrontando il triangolo primitivo ABC con ABC’, tenendo conto che gamma=gamma’, che epsilon =epsilon’, si vede chiaramente che la somma degli angoli del triangolo ABC è data da epsilon + lambda + beta + gamma; la somma nel triangolo ABC’ è: beta + gamma’ + epsilon’ + lambda; ne deriva che le due somme sono rigorosamente uguali.

 

Inoltre il triangolo ABC’ ha un angolo che è minore od uguale alla metà di uno degli angoli del triangolo di partenza ABC. Infatti la retta AC’ divide l’angolo alfa del triangolo ABC in due parti epsilon e lambda in generale diverse; una cioè lambda, è comune ai due triangoli e l’altra, epsilon è uguale ad un angolo, epsilon’ del nuovo triangolo ABC’. Nel nuovo triangolo allora ci sono due angoli, epsilon’ e lambda che sommati danno alfa, angolo del triangolo primitivo. Se sono uguali, caso poco frequente, si può affermare che il nuovo triangolo ABC’ possiede un angolo che è la metà di alfa e, se sono diversi, caso più frequente, il nuovo triangolo possiede un angolo minore della metà di alfa. Concludendo, vedere lo scritto ‘arruffato’ sulla figura

“qualunque cosa accada, potremo concludere che il nuovo triangolo possiede un angolo che è minore o al più uguale alla metà di alfa” M. Galli  opera citata.

Ma la costruzione fatta su ABC possiamo ripeterla su ABC’ ottenendo un terzo triangolo su cui applicare lo stesso ragionamento e così via. Supponendo di fare n costruzioni analoghe potremmo ottenere alla fine un triangolo che ha la stessa somma degli angoli come l’originale ABC e un angolo molto piccolo, minore od uguale a alfa/2^n, dove alfa è l’angolo del triangolo ABC di partenza.

 

CONCLUSIONI DEL TEOREMA DI ADRIEN LEGENDRE (1752-1833) CHE DEFINISCE GLI INCASTRI POTENZIALMENTE NECESSARI ALLA NASCITA DELLE GEOMETRIE NON EUCLIDEE, SITUATI SULLA ‘SUPERFICIE’ DEL TERZO MONDO DELLE ‘IDEE’ DI POPPER

Tenendo conto del teorema precedente, ammettiamo, per assurdo, che la somma degli angoli del triangolo ABC sia maggiore di due retti anche di una quantità molto piccola delta.

SOMMA ANGOLI DI ABC = 2 retti + delta

Nella costruzione precedente a triangoli successivi la somma dei loro angoli non può cambiare per postulato iniziale e così anche il valore della somma nel triangolo finale, di cui un angolo diventerà così piccolo da non superare alfa/2^n e gli altri due angoli insieme saranno minori di due retti, come dimostrato precedentemente, senza usare il V° postulato. Se n è così grande da rendere alfa/2^n minore di delta avremo che :

SOMMA ANGOLI DI ABC < 2 retti + alfa/2

asserzione che contraddice la formula precedente. Ne consegue che la somma degli angoli di un triangolo non può mai superare 2 retti! Si apre ora così la possibilità per le due affermazioni accennate all’inizio.

1 – La somma degli angoli di un triangolo è uguale a due retti.

2 – La somma degli angoli di un triangolo è minore di due retti.

Ma nascosto nelle pieghe del nostro teorema esiste un postulato euclideo fin’ora taciuto! Il susseguirsi delle nostre costruzioni sarebbe stato impedito dalla lunghezza della retta, in quanto se AM, che aumenta con n, non potesse essere raddoppiato sul suo prolungamento il processo si interromperebbe. Il postulato euclideo da focalizzare afferma che la retta è infinita! Una ‘retta’ disegnata su una sfera invece ha lunghezza finita, anche se illimitata, aprendo la possibilità per i triangoli sferici di avere la somma degli angoli interni maggiore di 2 retti.

GEOMETRIA E SCIENZA FISICA

Dal punto di vista della scienza fisica, l’interesse non va alla geometria non-euclidea come tale ma al notevole effetto che ebbe sul concetto di spazio nella fisica moderna. Non solo essa condusse ad una migliore comprensione della natura ipotetica della geometria assiomatica pura, ma alla chiarificazione del concetto di spazio fisico rispetto allo spazio matematico. Con la scoperta della geometria non euclidea fu chiaro che non esistevano mezzi a priori, cioè dal punto di vista logico matematico, quale tipo di geometria avrebbe descritto le relazioni spaziali fra i corpi fisici. Era naturale quindi interpellare l’esperimento per stabilire se il problema della vera geometria poteva essere deciso a posteriori. Per la misura degli angoli bisognava rivolgersi ai movimenti astronomici per ovviare ad errori di misura. Riemann parlò di spazio generalizzato di cui la geometria euclidea, quella ellittica di Lobacevsky e Bolyai e la sua sferica erano casi particolari, dando impulso allo sviluppo della moderna analisi tensoriale, che confinata fino ad allora ai problemi di elasticità, divenne un mezzo essenziale sia per la matematica superiore sia per la fisica teorica.

_____________________________________

Siamo giunti così nella zona storica di transizione alle Geometrie non euclidee, l’iperbolica di A. Bolyai (1802-1860), Nicolai Ivanovic Lobacevsky (1793-1856), e la geometria sferica di B. Riemann (1826-1866) e con questo terminiamo, e per entrare nel vivo di questo nuovo ambiente culturale vedere anche il post riportato in questo blog dal titolo ‘Geometria e Natura’, a più voci.

Dott. Piero Pistoia

CHI E’ L’AUTORE (traccia): CURRICULUM DI PIERO PISTOIA

 

piero-pistoia-curriculumok-1-28Download

POMARANCE: UNA BREVE PASSEGGIATA FLORISTICA A SCANSIONE MENSILE, PARTE QUINTA; a cura di Sofia, esperta sul campo e brava fotografa; coordinatore Piero Pistoia (NDC)

POST DA RIVEDERE E CORREGGERE

N.B. – SE NON ESPLICITATO ALTRIMENTI, TUTTE LE FOTO, PROGETTI, SCRITTI, ARGOMENTAZIONI E COMMENTI SONO DEL COORDINATORE PIERO PISTOIA

Continua il monitoraggio botanico-educativo delle piante selvatiche, a scansione mensile, lungo un percorso, alla periferia del paese di Pomarance, che, inserito nel paesaggio floristico della Val di Cecina, ne riflette le sue caratteristiche botaniche essenziali. Data la vicinanza delle Scuole, potrebbe, nel tempo, se mai la Buona Scuola diventerà attiva, essere utilizzato anche per passeggiate scolastiche culturali ad uso didattico – infatti la comunicazione non sarà meramente descrittiva, ma spesso inserita in un processo costruttivo di ricerca/scoperta, cioè nei  contesti delle OSSERVAZIONI SCIENTIFICHE scolastiche – e in generale come stimolo all’osservazione guidata della Natura Spontanea della zona, e non solo (se è vero che tutta la vegetazione italiana e delle Nazioni limitrofe, circa alla stessa fascia di latitudine risente mediamente del clima dell’area mediterranea). Questa comunicazione culturale gratuita può così ravviare il concetto di diversità biologica e attivare una interazione più diretta e positiva con il mondo della Natura.

CURRICULUM DI PIERO PISTOIA

piero-pistoia-curriculumok (#)

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

 

PER CHIARIRE, LE PARTI DEL COORDINATORE INIZIANO CON LA SIGLA ‘NDC’ E TERMINANO CON        ‘FINE NDC’, a guisa di INTERMEZZI  SU RIFLESSIONI, NUOVE PROPOSTE, ARGOMENTAZIONI E COMMENTI . TUTTO CIO’ INFATTI CHE NON E’ COMPRESO FRA QUESTE DUE SIGLE E’ OPERA DELL’INGEGNO DI SOFIA! 

____________________________

NDC Piero Pistoia

L’alto numero di foto in GIUGNO in successione lineare, ci costringe a ripartire da LUGLIO 2016 nella QUINTA PARTE.

COME NELLE ALTRE  PARTI I TESTI QUALIFICATI DI RIFERIMENTO PER QUESTO LAVORO SONO PRINCIPALMENTE I SEGUENTI  (consigliamo i lettori di  procurarseli per i riferimenti, l’approfondimento e la qualificazione delle biblioteche personali!)

EUGENIO BARONI “GUIDA BOTANICA D’ITALIA” Ed. CAPPELLI

PIETRO ZANGHERI “FLORA ITALICA Vol. I-II-III” Ed. CEDAM        

SANDRO PIGNATTI “FLORA D’ITALIA Vol. I-II-III” Ed. EDAGRICOLE

EDUARD THOMMEN “ATLAS DE POCHE DE LA FLORE SUISSE” EDITIONS BIRKHAUSER BALE.

N.B. – Il testo precedente di THOMMEN è stato perduto e sostituito dal testo acquistato ad hoc:

E. THOMMEN e A. BECHERER con lo stesso titolo, ma con EDITORE, SPRINGER BASEL AG; più recente, comprende anche le nazioni straniere limitrofe. Si tratta della sesta edizione redatta da Aldo Antonietti. 

VENGONO ANCHE CONSULTATE DUE GROSSE ENCICLOPEDIE SUL REGNO VEGETALE, L’UNA EDITA DA VALLARDI E L’ALTRA DA RIZZOLI; E SVARIATI ALTRI TESTI SECONDARI DI DIVERSE CASE EDITRICI CHE NOMINEREMO QUANDO NECESSARIO.

A questi testi si farà continuamente riferimento esplicito e si spera che Autori ed Editori permetteranno di trasferire qualche disegno schematico di chiarimento dai loro testi a questo post, il cui unico obiettivo è e rimarrà solo quello di ‘costruire’ e comunicare didatticamente cultura, per quanto ci riesce, sempre del tutto gratis. Questo blog non ha alcun fine di lucro ed è auto-finanziato. Comunque siamo disponibili nell’immediato a qualsiasi intervento su questo post su avvertimento (al limite, se necessario, anche a sopprimerlo!)

Il testo teorico di riferimento sarà:

Carlo Cappelletti “BOTANICA, Vol.  I° e Vol II°”, UTET

NOTE DEL COORDINATORE SU UNA PIANTINA, PER NOI,  DI NON FACILE CLASSIFICAZIONE (Inula conyza)

Chi volesse da subito gettare uno sguardo alla storia e alle caratteristiche della pianticella Inula conyza, oggi in fiore presso il Podere Ponsino, può cliccare sulla seguente espressione ‘calda’:

Inula conyza

Per anticipare, l’Inula conyza è una composita che, in pieno inverno, si presentò in alcuni punti del percorso (circa nella zona dove oggi, a fine luglio, è finalmente fiorita) con grandi rosette di base molto vegete, che, però, furono presenti per qualche mese e poi regredirono e scomparvero (seguono Foto di P. Pistoia).

 

 

Foglie di base peduncolate

Le prime ipotesi (una Primulacea o una Borraginacea…) risultano poco probabili e molto a rischio (Popper avrebbe detto ‘molto’ scientifiche in quanto facilmente falsificabili).  In effetti ci sono voluti molti mesi di attesa, fino alla sua fioritura in luglio, per poter individuare con sicurezza la famiglia (Composite) e poi il genere e forse la specie. Bisogna dire che solo l’intuitiva Sofia, già allora, pensava ad una Asteracea ed aveva ragione.

________________________

L’Epilodio è un’altra piantina, fotografata in luglio nel fossetto sotto la grossa quercia di riferimento a tre tronchi, sulla quale è possibile raccontare una storia sul processo di classificazione; per vederne l’inizio della storia e gli aspetti più significativi cliccare sotto su “EPILODIO”, che rimanderà poi anche alla PARTE QUARTA.

EPILOBIO

Oggi 30 luglio di sabato rimane forse solo una piantina vegeta di Epilobio sotto la quercia a tre tronchi. Da tempo esiste ancora una piantina di I. conyza, di piccola taglia, che sta fiorendo, sempre nella discesa verso il Mirto, poco dopo la grossa quercia cava, sulla sinistra proprio davanti ad una entrata nella vigna (sotto strada a destra).

Il 4 di Agosto quella solitaria piantina di Epilobio sotto la quercia di riferimento presenta ‘esplosi’ tutti i suoi frutti.

VIENE TRASFERITO IL MEMORABILE LAVORO FOTOGRAFICO E  DI CLASSIFICAZIONE  DI SOFIA ANCHE PER IL MESE DI LUGLIO 2016, RELATIVO AL PERCORSO SCELTO.

FINE NOTE DEL COORDINATORE

_______________________________________

LA CENTAUREA solstizialis

Centaurea solstizialis: <- clicca per vedere dove di trova la C. solstizialis.

__________________________

NDC  Piero Pistoia su C. solstitialis:  Spina gialla o Calcatreppola; fusti diffusi o ascendenti, raramente eretti con tomento ragnateloso; rami abbondanti alati; foglie scabre verde-grigie, le basali a contorno spatolato, pennato-lobate o pennato-sette a 2-3 lobi per parte; foglie cauline lanceolate, semiamplessicauli; capolini (2.5-3 cm) con involucro piriforme (10 x 12 mm), squame largamente ovate, terminate da spine robuste; fiori gialli, gli esterni fino a 2 cm; acheni neri 2.5 mm con pappo fino a 5 mm.

Leggere in Zangheri, opera citata

Centaurea solstitialis

5676 – capolino e foglia basale

5677 – brattea involucrale

Da Pignatti, opera citata:

Da Thommen e Becherer, opera citata:

2850 – CENTAUREA Solstitialis

FINE NDC

____________________________________

IL CLINOPODIO

Clinopodium nepetea: <- clicca per vedere dove si trova.

__________________________

INULA viscosa e PULYCARIA dysenterica

Enula viscosa: clicca per vedere dove trovarla nel percorso.

INULA viscosa (Dittrichia viscosa); N.B. – HO CORRETTO IL NOME DEL GENERE (?)

Talmente viscosa che riesce a trattenere un malcapitato ragno e i pappi delle asteracee vicine.

Non è ancora nel periodo della fioritura, a differenza di una pianta vicina, che talvolta si mescola insieme e diventa confondibile: la Pulicaria dysenterica, che già mostra i suoi capolini gialli.

Ho fotografato questi gruppi di piante, nel tratto di discesa verso il Mirto, poco sotto la quercia di riferimento.

PULICARIA dysenterica

________________________________

DIPSACUM fullonum (CARDO DEI LANAIOLI)

______________________________

EPILOBIO

EPILOBIO

Epilobium: clicca per vedere dove trovare nel percorso il cardo e l’epilobio

Dipsacum follonum:

Sempre lungo la discesa verso il Mirto, anche questa volta ho fotografato il Cardo dei lanaioli (Dipsacum follonum) durante la piena fioritura.

Epilobium:

Con minor successo ho cercato nuovamente di fotografare pure l’Epilobium col suo curioso piccolissimo fiore all’apice del baccello.

_________________________________

NDC Piero Pistoia : Per precisazioni sulla storia della classificazione e ipotesi sulla specie di questa pianticella della famiglia delle Onagraceae (EPILOBIO), vedere la PARTE QUARTA, cliccando all’inizio sul link interno EPILOBIO.

 

 

Da OSSERVARE NEL TESTO DI  E. Thommen; 1866 Epilobium angustifolium; ho perduto il testo originale del 1961; questo schizzo sbiadito è stato ripreso da E. Thommen  e A. Becherer del 1993, testo , pure originale, che riporta purtroppo schemi più sbiaditi!

FINE NDC

_______________________________

FOENICULUM vulgare

Foeniculum vulgare: <- clicca per vedere dove si trova.

Foeniculum vulgare

Anche questa pianta è presente in diversi punti del percorso.

Le foto riguardano la discesa verso il Mirto, che in questo periodo assolato offre la maggior varietà di tutte le specie che cerchiamo di individuare ed elencare.

____________________________

OSSERVAZIONE DI PICCOLI FRUTTI DI ARBUSTI

Osservazione piccoli frutti di arbusti

Osservazione piccoli frutti di arbusti

Osyris alba: il piccolo arbusto, mostra le sue bacche ancora verdi. Si trova all’inizio percorso sul lato dx della strada. (Argine tufaceo, vicino alla Nepitella)

Prunus spinosa: la pianta si trova in vari tratti del percorso. La foto si riferisce a quella sul lato sx all’inizio discesa del Mirto, praticamente insieme alle more. Anche se le piccole ‘prugnole’ mostrano un bel colore violaceo, la loro maturazione avverrà in autunno inoltrato, malgrado il sapore rimanga ugualmente asprigno. (Buone per liquori e marmellate)

Rosa arvensis: dopo i bei fiori profumati che accompagnavano ogni nostra visita al percorso, la pianta mostra orai suoi frutti ancora verdi, con la tipica sporgenza legnosa che favorisce l’identificazione della specie. (Foto davanti Sant’Anna)

Rubus fruticosus : ancora acerbe le sue more, cominciano a colorarsi leggermente di rossastro. (Foto inizio discesa Mirto, lato sx)

_____________________________

Inula conyza

INULA conyza

Inula conyzae: <- storia di una classificazione di Sofia

Inula conyza

Questa pianticella che ci ha tenuto nell’incertezza per la sua identificazione fin dall’autunno-inverno dello scorso anno, finalmente sta sbocciando i suoi capolini.

(………..bene o male avevo capito a suo tempo che si trattava di un’Asteracea!….)

Le foto si riferiscono alle piante che si trovano vicine al Ponsino, sia sul lato dx che sx della strada.

_______________________________

NDC  Piero Pistoia – Si tratta di piante con foglie basali grandi picciolate e con foglie cauline non decorrenti, ma a base cuneata più piccole delle basali,  a pagina inferiore finemente tomentosa; fusti e gli involucri dei capolini, più o meno rossastri, i fiori periferici sono praticamente prive di ligule.

 

VEDERE LO SCHEMA DA: S. Pignatti “Flora Italica Vol. III”, EDAGRICOLE

5104 I. bifrons; rametto fiorito e foglia inferiore

5105 I. conyza ; foglia

E LO SCHEMA DA P. Zangheri “Flora italica II”, CEDAM

FINE NCD

____________________________

LACTUCA serriola

Lactuca serriola <- dove si trova nel percorso.

Lactuca serriola

Si trova qua e là in vari punti del tragitto, ma le foto di si riferiscono alle piante che spuntano pochi metri dopo l’ingresso della residenza San Domenico, sull’argine dx vicino ai cipressi.

La pianta, confondibile con altre specie commestibili, è in realtà un poco tossica e il suo latice appiccicoso, può essere urticante per le pelli sensibili e per le mucose.

________________________________

Osservazione di varie forme di…

Osservazione di varie forme di ‘contenitori’ di semi di piante erbacee:

Filipendula, osservata sempre nella discesa Mirto.

Scabiosa columbaria, fotografata vicino alla rete che costeggia il pelago, dove tuttora è in piena fioritura.

Silene alba, il suo curioso contenitore a palloncino sembra abbia dato il nome alla pianta, in quanto Sileno compagno di bevute di Bacco, si narra che avesse una pancia che ricordava la forma del frutto di questa specie. Fotografata vicino al margine dell’oliveta, lato sx strada, inizio percorso.

____________________________

VERBASCUM sinuatum

Verbascum sinuatum

Verbascum sinuatum

Le foto riguardano il gruppo di piante nello spazio sul lato dx della strada, davanti Poggio Bartolino (credo si chiami così casa Fontanelli).

____________________________________

NOTE DEL COORDINATORE (NDC)

Nel corso dei mesi, ma specialmente col passare degli anni  potrà accadere che il pezzo di cammino scelto per lo studio floristico di pianticelle selvatiche (erbacce), cambi di aspetto, ma certamente le informazioni botaniche  offerte relative ad esso, che dipendono essenzialmente da ragioni astronomiche, continueranno a ‘vivere’ nella memoria infinita di internet praticamente per sempre, per cui anche in un futuro molto lontano potrebbe avere senso per quegli umani poterle riutilizzare in qualche modo. Così riteniamo che sia probabile che questo esperimento venga a configurarsi come una via aperta a svariate possibilità  per studiare la Natura.

FINE NDC

_______________________________________

I PRIMI DI AGOSTO,  LE FOTO DI SOFIA e relativi commenti

Acero tribolo commento in testo

_________________

CHENOPODIUM album

Chenopodium album commento in txt

_______________________

CLEMATIS vitalba

Clematis vitalba commento in txt

_________________________

DAUCUS carota

Daucus carota commento in txt

__________________________

Galatella linosyris commento in txt

Inula conizae commento in txt

LEGGERE in Thommen e A.Becherer 1993; 2682 Inula conyza

_______________________

LEPIDIUM graminifolium

Lepidium graminifolium commenti in txt

____________________________

NIGELLA damascena

Nigella damascena commento in txt

______________________________

RUMEX crispus

Rumex crispus commento in txt

ANCORA IL LAVORO FOTOGRAFICO  SUL CAMPO E BREVI COMMENTI DI SOFIA  DATATI IL I° SETTEMBRE 2016

piante-osservate-il-giorno-1-settembre : se ci clicchi ottieni il testo di Sofia che segue 

Piante osservate il giorno 1 settembre.

Nonostante i due giorni di pioggia, il percorso preso in considerazione per l’osservazione delle piante, mostra quasi esclusivamente graminacee secche lungo i bordi della strada e nei campi adiacenti.

Perlustrando con maggiore attenzione, sono riuscita a trovare qualche eroica specie sopravvissuta al ventoso caldo estivo del mese di agosto.

Chenopodium album: già fotografato nelle ultime osservazioni, ora grazie alla vicinanza del grosso mucchio di letame, di fronte alla residenza del Ponso, è notevolmente cresciuto.

Coniza bonariensis (Erigeron bonariensis). Non di certissima identificazione, anche questa piantina infestante su tutto il percorso, ha resistito al calore estivo. Le foto si riferiscono a quella vicino al letame, che la fa crescere vigorosa.

3 Asteracee a confronto. Molto simili, queste tre specie le ho osservate sul lato dx della strada, lungo la discesa che dal Ponso, porta a San Domenico.

Inula viscosa: capolino giallo, come le altre e foglie appiccicose che la contraddistinguono.

Pulicaria disenterica: Molto simile all’Inula viscosa, talvolta i cespugli delle due specie crescono vicini da sembrare un’unica pianta.

Jacobea vulgaris, viene anche chiamato Senecio di San Giacomo. Prossimo alla fioritura. I capolini rassomigliano molto alle specie già descritte, ma le foglie sono totalmente diverse, ricordano quelle del crisantemo.

Bacche (Cinorrodi) di Rosa canina e Rosa arvensis: giunto il periodo di maturazione per entrambe le specie, si possono facilmente notare le differenze che aiutano per un sicuro riconoscimento delle due piante. Nella Rosa canina le infruttescenze, sono di forma piuttosto ovale-allungata, mentre per la Rosa arvensis si presentano più rotondeggianti e più numerose sul ramoscello, distinguibili soprattutto per i residui della colonna dello stilo. (Fotografati davanti la residenza S.Anna, nel cespuglieto sul lato dx della strada).

Rubia peregrina: di fronte a san Domenico, lato sx, aggrovigliata ad altre piante di rovo ho notato i piccoli frutti della Rubia ancora verdi, che saranno maturi in autunno.

_____________________________

Note del coordinatore P. Pistoia (NDC) – Per leggere le argomentazioni sulla classificazione della CONYZA bonariensis andare nella PRIMA PARTE dopo la cartina, e cliccare sul link  CONYZA o ERIGERON? Sembra che l’ERIGERON bonariensis non risulti nei testi controllati.

FINE NDC

_____________________________

Seguono le foto di Sofia

CHENOPODIUM album

CONYZA bonariensis

INULA viscosa

JACOBEA vulgaris

PULICARIA disenterica

ROSA arvensis

RUBIA peregrina

IL 19 SETTEMBRE SOFIA HA MANDATO IL SUO DIARIO FLORISTICO RELATIVO AL SOLITO PERCORSO. SEGUONO LE FOTO DELLE PIANTICELLE EMERGENTI ED IL SEGUENTE COMMENTO:

CLICCARE SU:

piante-osservate-il-19-settembre in Word

OVVERO LEGGERE IL CONTENUTO DEL LINK, di seguito

Cyclamen ederifolium:

Si trova soprattutto sul lato sx della strada, poco dopo l’inizio e prosegue fino a poco prima della traversa che porta all’oliveta. Questo Ciclamino, già descritto lo scorso anno è molto simile al Cyclamen repandum, che fiorisce invece in primavera, ha un colore più intenso ed è profumatissimo.

Parietaria officinalis:

Fotografata proprio sotto l’argine del podere Ponsino, vicino al tronco di un cipresso. Questa pianta officinale, dai molteplici utilizzi, viene sempre un po’ ignorata, dato che non è molto appariscente. In questo periodo prosegue la sua fioritura, che dalla primavera continua fino all’autunno.

Crataegus:

Tra le bacche che maturano in questo periodo, nelle siepi di arbusti di fronte al podere Sant’Anna, ho osservato quelle del ‘Biancospino’. (Non so se la specie sia ‘monogyna’ o ‘laevigata’. La prossima volta osserverò se il frutto abbia un solo seme o più)

Synphyotricum (NDC:  Symphyotricum ) squamatum :

Di fronte alla casa col pelago, nell’argine dx della strada spunta questa Asteracea dai fiori minuscoli. A lato della stessa casa ne ho osservata un’altra pianta piuttosto grande. Altre piante sono lungo la discesa che porta al Mirto (lato sx), poco dopo la quercia col tronco biforcato, che di solito prendiamo come riferimento.

Galatella linosyris:

Finalmente questa graziosa asteracea autunnale sta per rifiorire, proprio vicino al cartellino con la sua descrizione. Anche a pochi metri di distanza, sullo stesso argine ne sono spuntate numerose altre piante, che non erano presenti lo scorso anno.

Helianthemus (NDC: o Helianthus?) tuberosus:

Dopo San Sebastiano, sotto l’argine dx del piccolo slargo, dove la strada comincia a scendere per il Mirto, ho notato questa pianta che di solito colonizza zone con presenza di umidità. In effetti avvicinandomi, il luogo mi è sembrato che corrispondesse a tali caratteristiche, infatti poco più avanti sono presenti anche dei salici.

Verbena officinalis:

Prosegue la fioritura della piccola Verbena, fotografata proprio sotto la grande quercia, nella discesa verso il Mirto.

Cornus sanguinea:

Sempre nelle immediate vicinanze della quercia di riferimento, lato sx della strada, ho notato degli arbusti di Corniolo sanguinello, con le piccole bacche mature e le foglie che fin da ora stanno assumendo la caratteristica colorazione rossastra che ha determinato anche l’epiteto del suo nome.

SEGUONO LE FOTO DI SOFIA RELATIVE ALLE INFORMAZIONI PRECEDENTI

Cyclamen ederifolium

 

Parietaria officinalis

Crataegus (o biacospino)

 

Synphyotricum (NDC:  Symphyotricum) squamatum (?)

 

 

Galatella linosyris

Helianthus tuberosus (topinambur)

 

Verbena officinalis

 

Cornus sanguinea

 

Un insetto stecco?

_____________________________

NDC Piero Pistoia – Siamo ai primi di ottobre 2016 e rinascono timidamente le piantine della precedente primavera come il terracrepolo (l’Asteracea Richardia picroides); alcuni esemplari si notano davanti al podere Poderino, sull’argine per salire, sopra strada, al prato di S. Barbara.

Terracrepolo

Richardia picroides

Più numerose piantine che volg. chiamiamo  piscialletto o pisciacani , estremamente polimorfi (assomigliano ai terracrepoli) sempre in via del Poderino, scendendo verso sud, a destra nel campetto subito dopo il confine con la proprietà Borghetti, prima dell’incrocio con via dei Filosofi. così ad occhio potremmo rischiare come primo tentativo di ipotesi che si tratti di Taraxacum officinale, visto che in gergo i piascialletto si chiamano anche tarassachi.

Taraxacum officinale (?)

Taraxacum officinale (?)  (capolini, lunghezza caule, forma foglie della rosetta basale, radice, boccio). Petali periferici arrossati all’esterno. La radice spesso sembra si divida all’inizio.

 

Taraxacum officinale (?) (lunghezza caule unico dei campioni, max=40-45 cm). Impossibile osservare ora  gli acheni, necessari alla classificazione. Seguiremo la fruttificazione.

DESCRIVIAMO ORA I CAMPIONI OSSERVATI: aspetto erbaceo;  da una radice tendenzialmente a fittone partono alcuni fusti semplici (spesso uno solo) (max 40-50 cm) poco ramosi (1 o 2 volte biforcati), fogliosi in basso , con foglie inferiori sinuate o pennato-lobate, le altre cauline, più rare, lanciolate abbraccianti intere o dentate; squame  dell’involocro esterno, cuoriformi alla base; capolini gialli, talora con ligule periferiche leggermente macchiate, rigonfi alla base poi cilindrici.

CARATTERISTICHE DEL TARAXACUM officinale

Il tarassaco officinale è un gruppo estremamente polimorfo, con radice a fittone dapprima indiviso poi ramificato. Al colletto della radice si avvolgono squame brunastre o nerastre. Foglie con nervature reticolate, grossolanamente dentate o lobate; raramente intere, ma anche incise fino alla nervatura centrale; si restringono in un picciolo talora alato; capolini  grandi 2.5-4 cm; uno o più cauli  (15-30 cm), glabri, per ogni radice partono dalla rosetta, scapi cavi, lattiginosi che portano alla cima ciascuno una inflorescenza a capolino giallo-dorato; squame involucrali esterne lineari, generalmente ripiegate verso il basso.

Da OSSERVARE IN  E. Thommen e A. Becherer : 2919 – Taraxacum officinale (dent-de-lion). Abbozzo di radice, rosetta di base, seme con pappo, squame involucrali e capolino

Intanto confrontando le caratteristiche del campione osservato con la scheda del T. officinale, rileviamo alcune discordanze (nel campione notiamo cauli più brevi, foglie senza nervature reticolate, petali periferici arrossati all’esterno e le squame involucrali non sono inflesse verso il basso e, nei casi osservati, per ogni radice usciva un solo caule); e’ probabile che l’ipotesi sia falsa. Forse potrebbe trattarsi di un Dente di Leone (genere Leontodon) od altro. Vedremo.

FINE NOTE DEL COORDINATORE

_________________________________________

Il link classifica le piantine fotografate nei diversi punti del percorso

percorso-del-3-ottobre-2016

Contenuto del link precedente:

Percorso del 3 ottobre 2016

1. Linaria vulgaris: all’inizio del percorso è visibile sulla dx un bel cespuglio fiorito di questa specie. I suoi steli eretti e snelli, portano fitti racemi, al termine dei quali si aprono graziosi fiori gialli a forma di fauce. 4 foto.
2. Cornus sanguinea: insieme alla Linaria, incurante dell’autunno, si può osservare una vistosa fioritura di un cespuglio di Corniolo sanguinello, con ramoscelli e getti nuovi pieni di foglie ancora verdi. Foto 3
3. Amaranthacea: proseguendo il cammino, vicino al tronco di un cipresso, proprio davanti all’entrata del Ponsino (lato sx della strada) ho notato questa Amarantacea, di cui per ora non è del tutto definibile la specie. Foto 3
4. Verbascum blattaria: piccola piantina, in questo momento con unico fusto eretto, vicino al bordo dell’asfalto. Si trova sul lato dx della strada a circa una ventina di metri dopo l’ingresso di sant’Anna.Foto 3
5. Portulaca oleracea: Pianta invasiva commestibile, con le sue foglioline carnose e i rametti rossastri prostrati e striscianti. Si trova proprio accanto al piccolo Verbasco e credo di non averla mai notata prima, in questo percorso. Foto 7
6. Galatella linosyris: completa fioritura per questa Asteracea che ha colonizzato gran parte dell’argine vicino al suo cartellino descrittivo. Appare inoltre anche lungo la discesa che dal Ponso va a San Domenico (lato sx). Foto 5
7. Carex pendula: sempre sul lato sx della via, di fronte alla residenza San Domenico, alla base del capannone di canne, si apre uno spazio che lascia intravedere anche un bel panorama sulla campagna circostante. Proprio qui si trova questa Cyperacea, con dei bellissimi cespugli eretti e vigorosi. Foto 5

8. Asparagus acutifolius: nella discesa verso il Mirto, sul lato dx della strada, spunta questa pianta che ci mostra le sue piccole bacche verdi, non ancora mature. Foto 3

1 -Linaria vulgaris

2 – Cornus sanguinea

3 – Amarantacea

4 – Verbascum blattaria

5 – Portulaca oleacea

6 – Galatella linòrysis

7 – Asparagus acutifolius

8 – Carex pendula

PIANTICELLE SPONTANEE FOTOGRAFATE DA SOFIA IL 19 OTTOBRE  2016

CLICCARE SOTTO PER VEDERE IN TXT IL SUO COMMENTO

percorso-del-19-ottobre

3 foto di Cicorium intybus

______________________

5 foto di Uruspermum dalecampii

________________________

3 foto di Soncus oleareus

_________________________

4 foto di Reicardia picroides

INIZIO NDC (note del coordinatore)

VEDERE SCHEMI DI Reicardia picroides

DA PRECISARNE I RIFERIMENTI E COMMENTI NELLE O. C.

IN S. Pignatti

E VEDERE IN P. Zangheri

395 – Capolini di R. picroides

5895 – Capolino di R. picroides; 5896 – Pianta di R. picroides; 5897 – Frutto di R. tingitana; 5898 – Foglia caulina di R. picroides, susp. intermedia.

…….. E schema del T. officinale da Thommen

Che cos’era la pianticella delle Asteraceae, osservata all’inizio di ottobre,  di cui abbiamo fatto l’ipotesi a rischio: Traxacum officinale? E’ una Ricardia picroides? O un dente di Leone? O…… Confrontiamo i suoi  schemi e la sua descrizione dai testi, con le osservazioni sulla pianticella precedentemente fotografata dal coordinatore, che la propose fortemente incerta come ipotesi iniziale.

1 – E’ necessario fare la descrizione diretta del campione osservato, cioè fare una prima scheda provvisoria con le caratteristiche botaniche notate, guardando direttamente la piantina in posto e osservando le foto. Se la piantina è incompleta descrivi quello che vedi! Se non si ricava nessuna caratteristica si passa ad un’altra piantina e l’altra si osserverà in futuro.

2 – Da questa  prima descrizione si formula l’ipotesi che in generale sarà incerta.

3 – Ora si passa al controllo (EE di Popper). Con l’ipotesi dai testi o appunti (o ricordi) descrivi  le ‘vere’ caratteristiche della piantina ipotizzata (seconda scheda) e guardi se ci sono differenze e dove sono con la prima scheda ipotetica;  individuare dove sono le differenze aiuteranno a formulare le ipotesi successive, se ci sono.

4 – Da questo controllo evinci se l’potesi è corroborata o falsificata.

Da continuare l’argomentazione….

FINE NOTE DEL COORDINATORE

____________________________

3 foto di BORRAGINE

______________________________

6 foto della Rubia peregrina

__________________________________

5 foto di RUBIACEA

_____________________________________

CONTENUTO DEL FILE DI TESTO DEL 19 OTTOBRE

Percorso del 19 ottobre

L’autunno è abbastanza avaro di nuove piantine da osservare.

Mi ha incuriosito la rassomiglianza di alcune piante, tra l’altro commestibili e ho cercato con qualche foto di metterle a confronto.

1) Cicorium intybus

2) Uruspermum dalechampii

3) Soncus oleraceus

4) Reicardia picroides

5) Inoltre ho notato diverse piante di Borragine, che cominciano a spuntare di nuovo, soprattutto nel luogo dove era posizionato il cartellino identificativo. (sotto l’argine dx della strada, appena oltrepassato il Ponsino)

6) Spunta di nuovo anche la Mercurialis annua con i timidi fiorellini bianco-verdastri. (proprio vicino alla Borragine)

7 – 8) Due Rubiacee a confronto. Sicuramente una è la Rubia peregrina, già osservata la scorsa primavera, con le sue foglie coriacee, appiccicose e pungenti e il suo stelo quadrangolare. Mentre l’altra, dall’apparenza molto simile, ma di consistenza più erbacea, potrebbe essere un’Asperula o con probabilità un Galium laevigatum……chissà? Aspetteremo la fioritura, per poterle osservare ancora meglio. (Anche questa sull’argine dx della strada sotto la filata di cipressi, vicino alla Borragine).

SOFIA

_______________________________

NDC – Piero Pistoia,

nella passeggiata PARTE SECONDA vicino all’inizio del post già fotografò queste due Rubiaceae su cui espresse dubbi,  chiariti ora da Sofia: si tratta di due generi diversi : la coriacea Rubia peregrina e l’altra erbacea, più delicata, apparterrebbe ipoteticamente al genere Asperula o al genere Galium; per la seconda ha ipotizzato anche la eventuale specie, G. levigatum.

 

Il 10 ottobre del 20015 sull’argine all’inizio della proprietà S. Anna fotografai campioni  forse di asperula ‘nascente’ e ‘matura’; allora scrissi,  sul campione osservato, “si nota un fusto quadrangolare, la successione ai nodi di verticilli di 6-8 foglioline oblunghe lanceoloate e uninervie; presenza di ramoscelli all’inizio dei verticilli. Nelle ‘adulte’ le foglie ai verticilli sono meno numerose (max 6) e puntate; le adulte hanno l’aspetto più massiccio. Qui si precisa che si tratta di due specie diverse.

 

IN TOMMEN E BECHERER o.p. citata

2494 – Asperula arvensis

2497 – Galium glaucum

2518 – Galium sylvaticum

2519 –  Galium pumilium

2524 – Galium mollugo

2525 – Rubia peregrina

da continuare l’argomentazione sui testi per il controllo!

fine NDC

IN CORSO DI PUBBLICAZIONE….

piero-pistoia-curriculumok (0)

e.c. sostituire a EPSS, SPSS

EPISTEMOLOGIA, PSICOPEDAGOGIA, INSEGNAMENTO DELLA FISICA E RIFORMA DELLA SCUOLA a cura del dott. Piero Pistoia; post aperto a più voci.

EPISTEMOLOGIA, PSICOPEDAGOGIA E INSEGNAMENTO DELLA FISICA NELL’OTTICA DI UNA RIFORMA SCOLASTICA 

a cura del dott. prof. Piero Pistoia

TITOLI DEGLI ARTICOLI IN QUESTO POST

(1) – I fondamenti psicologici ed epistemologici dell’insegnamento della Fisica;  scritti di Piero Pistoia e Andrea  Pazzagli

(2) – I processi di ‘comprensione’ e la loro utilizzazione per  l’insegnamento di un concetto fisico: scritto del dott. Piero Pistoia

(3) – I fondamenti psicologici ed epistemologici della Riforma Scolastica. scritti di Andrea Pazzagli e Piero Pistoia

I TRE INTERVENTI, SCRITTI NELL’INTERVALLO FINE 1977 – INIZIO 1980, NACQUERO, ALCUNI,  DALLA COLLABORAZIONE FRA UN MAESTRO DELLA SCUOLA PRIMARIA ED UN DOCENTE DELLA SCUOLA SUPERIORE E FURONO PUBBLICATI DALL’EDITORE LOESCHER NELLA RIVISTA QUINDICINALE, ‘LA RICERCA’, AD ALTA DIFFUSIONE NELLA SCUOLA SUPERIORE.

Gli autori ritengono che i concetti e processi qui riportati, per alcuni versi, possano essere considerati ancora attuali e rilevanti, vista anche la direzione-redazione universitaria della rivista (Maria Corda Costa,  Elena Picchi Piazza ed altri), dove furono pubblicati ( da immettere le coordinate precise delle riviste interessate)

EPISTEMOLOGIA_E_FISICA0001 (1) (2)

EPISTEMOLOGIA-FISICA0001 (3)

Gli articoli qui riportati sono stati considerati rilevanti ancora oggi dalla dott.ssa Manuela Vecera, psicologa psicoterapeuta.

 Vedere su questo blog anche altri interventi di Piero Pistoia, su proposte di varie lezioni scolastiche ed altro, in particolare:

   IL MONDO DELLA SCUOLA ED IL MONDO DEL LAVORO: un rapporto difficile

Curriculum di piero pistoia:

piero-pistoia-curriculumok (0)

CONTROLLA IL CONTO! ESEMPIO DI ANALISI STATISTICA CON EXCEL SU PIOGGE E TEMPERATURE MENSILI NEL VOLTERRANO – sia usando R per piogge 1956/1986, sia direttamente con Excel, 1956/1961 – del dott. Piero Pistoia

 

piero-pistoia-curriculumok-1-79Download

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

POST IN VIA DI COSTRUZIONE: LA VIA SI FA NELL’ANDARE! e, con Foerster e, per certi versi, Bruner, la cultura non si comunica ma si costruisce insieme.

Per questo lavoro si ringrazia il dott. David Bettini per aver fornito nel 1996, circa venti anni fa, i  dati mensili di piogge e temperature del Volterrano per trenta anni a partire dal 1956

Da aggiungere l’analisi direttamente con Excel per piogge 1956-1961

RIFLESSIONI E CONTI  SU PIOGGE E TEMPERATURE MENSILI DAL 1956 AL 1986, CALCOLO E VARIAZIONE DEGLI  INDICI CLIMATICI DI BAGNOULS E GAUSSEN COL TEMPO,  ATTRAVERSO MEDIE MOBILI, FATTORI STAGIONALI ED ALTRO SULLE SERIE STORICHE a cura del dott. Piero Pistoia

Ecco i ‘conti’ con Excel che sviluppai appunto una ventina d’anni fa:

in xls:

PIOGGE_VOLTERRA 1956-1986

in pdf:

piogge_volterra1-1956-1986

Sulle cartelle di lavoro di Excel appaiono 7 grafici (N°: 1-2; 3; 4; 7; 8; 9; 11) e 7 fogli di lavoro (N°: 18; 1; 2; 3; 5; 6; 7), alla rinfusa a zibaldone, su cui discuteremo nel seguito.

I seguenti intervalli sono pagine bianche: 10-15; 24-25; 31-32; 38-39; 50-52; 70-75

Intanto il lettore potrà trovare una guida alla ‘lettura’ dei precedenti processi (individuando le formule utilizzate) su altri esempi di statistica, anche  con l’uso di Excel, dello stesso autore, per es. nel post “UN PARZIALE PERCORSO DI BASE SULL’ANALISI DI UNA SERIE STORICA REALE…”, uno zibaldone di statistica e linguaggi informatici (la statistica ‘raccontata’ con Excel, con il Basic, il Mathematica di Wolfram e l’R), ecc..

DA CORREGGERE IN DIVENIRE, PERCHE’ L’ARTICOLO SCIENTIFICO ‘RIPULITO’ E’ STATO CONSIDERATO SPESSO DA RICERCATORI AFFIDABILI UNA FRODE!

Intanto cerchiamo di ricavare dal link i dati di pioggia e temperatura in Excel, per memorizzarle in un file .csv, leggibile da R. Iniziamo con i dati di pioggia. Si clicca sul link: PIOGGE_VOLTERRA_1956_1986, riportato sopra.

Appare una console di Excel con riportate varie colonne, nominate sopra; si va al Foglio 1 (7 colonne e un grafico degli Effetti Stagionali) e si isola intanto la seconda colonna  che contiene 360 dati mensili della pioggia da 1956 al 1986, eliminando le altre, memorizzandola poi col suffisso .CSV, nel file VOLTERRA_PIOGGE_1956_1986_A (ricordarsi in quale Memoria di Massa), con le seguenti opzioni: Si mantenga il formato corrente – Tipo di carattere occidentale – Separatore di campo la “virgola”.

Si entra nella console di R e si guarda se il processo funziona.

setwd(“X:/”)

in X va la lettera della memoria di massa; nel nostro caso setwd(“I:/”) o ultimamente G-

Si fanno tentativi per far leggere da  R  i dati con suffisso .xls

Altri scritti e argomentazioni seguiranno successivamente

ECCO UN PRIMO ‘ASSAGGIO’ ORGANIZZATO DEL RACCONTARE  L’ARTICOLARSI DEL CONTENUTO DEL LINK IN XLS CON IL LINGUAGGIO DI R, INIZIANDO IN PARTICOLARE DALLA COLONNA DUE CHE CONTIENE I DATI .

In definitiva tenterò di raccontare una storia statistico-informatica usando un linguaggio informatico alternativo; i diversi trucchi informatici con i loro risvolti logico-razionali necessari aumenteranno la possibilità di tentare veloci prove diversificate, attivando una maggiore concentrazione sui concetti statistici, visti da punti di vista diversi, insieme alla loro memorizzazione e alla loro assimilazione, oltre ad un intenso ammaestramento informatico.

Come in un gioco di puzzle a più vie, si attivano costruzioni con i ‘mattoni’  statistici a più possibilità e si costruiscono gli stessi concetti statistici con ‘mattoni’ informatici diversi logicamente, individuando percorsi diversi  e il percorso spesso diventa una facility  per l’apprendimento.

SCRIPTS IN R E COMMENTI

setwd(“I:/”)
dataset=read.csv(“PIOGVOLTR0.CSV”, header=T, dec=”.”, sep=”;”). La lettera ‘0’  è uno zero!

#Da tener d’occhio l’attributo dec=”.” dell’argomento !?

#COME SI COSTRUISCE IL FILE PIOGVOLTR0.CSV a partire da foglio 1 di Excel:

# 1 – Dal post “CONTROLLA IL CONTO…” si carica, cliccando sul link
#”PIOGGE_VOLTERRA 1956_1986″, l’analisi in .xls su questi dati di cui parla il post
# e questo al fine di costruire dal foglio 1 un data frame leggibile da R.

# 2 – E’ un foglio di Excel, ma siamo in Open Office; mi pongo sul foglio 1
# (siglato anche col nome del link)

# 3 . Cambio le intestazioni originali e le sostituisco col nome di variabili neutre
#X.1 X.2 …X.7 per le sette colonne del foglio; ne chiariremo nel proseguio
#il contenuto.

# 4 – Salvo questo foglio in xls con l’opzione di Open Office “Testo CSV(.csv)”
# nel file, in questo caso, PIOGVOLTR0 che ricaricheremo con R; ognuno
#può chiamarlo col nome che vuole e memorizzarlo sul disco che vuole, basta
#ricordasi il nome; noi abbiamo chiamato il file come detto e lo memoriziamo in
# un disco rimovibile indicato con I o G. Durante la memorizzazione rispondiamo
#alle domande, separatore di campo “;” , separatore di testo Apice ‘ ecc.

# 5 – Si copi il presente testo sulla console di R e controlla che giri; il nostro gira! Per un po’!! Vedere nel proseguo dell’argomentazione.

Oppure, per  preparare i racconti successivi, si memorizzano tutte le sette colonne (cioè l’intera pagina di excel), ponendo al posto delle intestazioni che figuravano nella pagina, le seguenti sette una per colonna: X.1,X.2….X.7, alla testa di esse.

PREMESSA E DESCRIZIONE DEL PROCESSO

ECCO IL NOSTRO PROGETTO IPOTETICO CON OUTPUTS

attach(dataset)
X.1

Dovrebbe apparire  la prima colonna

Dovrebbero apparire i 6 valori iniziali del dataset

head(dataset)

X.2[1:6]

In effetti appaiono tre NA iniziali prima dei valori del 1956; per il resto Ok; con

X.2[4:375], si pensa di correggere; appaiono i 372 valori effettivi delle piogge misurate! La corroborazione dell’ipotesi sembrava abbastanza scontata. Il dataframe col processo descritto portava, nominando la seconda variabile di colonna, ai dati da analizzare! Il processo aveva funzionato.

Invece da qui la sorpresa non prevista. Se cerco di memorizzare  X.2[4-375] in una variabile (es.,dataset2 ), cioè

dataset2=X.2[4:375] e guardo i dati in essa (battendo dataset2 sulla console di R) i contenuti sono stranamente completamente cambiati! ts.plot(dataset2) dà un grafico che sembra non riguardare più la nostra prova, comunque continuiamo la loro analisi per cercare anche di capire. Il processo comunque è un modello abbastanza trasferibile ad altri insieme di dati! Poi con calma cercheremo di entrare in possesso di questi dati reali in qualche modo, al limite copiandoli direttamente in un vettore  di R. Insomma nel trasferimento del contenuto conosciuto di una variabile ad un’altra….entriamo in una zona caotica imprevista, almeno per ora. VEDREMO poi!

_________________________________________________________

ECCO IL RIQUADRO DELLO  SBAGLIO NON VOLUTO!

Da una revisione sui processi nella sintassi del  richiamo del file in .CSV, fra gli altri attributi, c’era dec (separatore dei decimali) =; qui fra virgolette avevo inserito il punto. Dovevamo dire che invece c’era la virgola: dec=”,”. Ora il programma gira. Col punto il programma pensava che le scritte dei numeri decimali fossero testo,  attivando le funzioni factor e level.

ECCO IL RIQUADRO DELLA CAUSA

I am sorry. Troppe direttrici culturali, aperte e diverse fra loro, da ordinare, creano una situazione entropica densa e dispersiva che, coniugata al tempo che ora scorre rapido ed ai problemi sempre più numerosi in quest’ultimo scorcio della vita, aumentano una richiesta di concentrazione poco spiegabile per un lavoro semplicemente hobbistico, in totale assenza di contributi, che vengono invece elargiti, per la cultura, da organi sociali; per passare il tempo insomma! Vedrò.

Comunque , ‘si parva licet componere magnis’ (Virgilio ‘Georgiche, IV), ritengo che un apporto culturale che non si esaurisca in ‘racconti e descrizioni’, ma proceda con punti interrogativi, caso proprio di questo blog, non sia inferiore a quello dei molti centri attivi benificiati da contributi, ed anche mi sembra che le stesse ‘lectiones magistrales’ dei gruppi di eccellenza, che si susseguono nei palchi, spesso, nel migliore dei casi, si ‘spengano’ in se stesse, comunicando poco, e, negli altri casi si riducano ad escamotages pubblicitari per ottenere finanziamenti.

In attesa …per i lettori curiosi, se ci sono, ho intanto ricopiato direttamente in un vettore di R i 372 dati delle piogge mensili, su cui sarà possibile accedere, nell’immediato, alla loro analisi, ‘divertendosi’ nel controllare conti e processi, cioè nel fare cultura. 

dataset=c(89.2,32,68,106,39.8,69.4,33.4,25.2,64.4,41.4,123.8,34.4,
66.8,100.2,17,109.8,159.8,23.6,27,5.6,2.4,74.2,100.8,79,
47.4,27,133,108.8,36,30.6,22,21,12.8,163.8,67,134.4,
61.2,35.6,133.2,69.2,120.8,25.4,4.6,46,46.2,74.6,73.4,149.2,
57.8,112.8,113.4,62,9.6,91.4,64.6,5.2,179.6,214.6,132.2,210.2,
107.8,30,0.6,152.8,37.6,73,18.4,1.5,87.6,160.4,135.8,86.4,
50.4,46.6,139.6,35.6,35.6,21.6,37.6,50,64.8,161.6,196.8,35.4,
147.6,89.4,75.3,74.2,45.8,89.2,28.8,38.8,94.6,95.2,100.4,88.8,
4.6,77.6,157.6,58.8,49.6,32.2,84,69.5,34,193,78,118.4,
127.8,16.8,91,107.4,50.4,36,80,24.8,119.8,2.6,240.2,104.8,
97.8,88.4,28.4,28.4,36.2,28.6,67.2,52.2,122.8,173.4,259,59.6,
49.2,42.2,56.4,11.4,84.2,83.6,19.4,75.8,99.2,42.8,99.8,62.6,
57,149.8,29.8,49,156,91.4,28,65.8,35.6,75,148.2,68,
89,156.2,85.8,40,56.6,43.4,38.4,83.8,128.6,26.4,157.2,106.4,
104.8,98.2,140.6,79.6,66.6,63.8,18.6,22.4,75,28.2,106.4,95,
81,51.4,55,53,122.4,67.2,15.8,2.2,54.8,17.4,149,8.6,
85.4,91.8,43,106.8,51.4,26,71,49,136.6,76,46.8,67.2,
70.8,33,13,48.2,17.2,56.2,38.8,22.6,171,80,73.2,30.6,
35.4,105.2,66,80.6,52.8,27.2,12.6,61.4,88.8,87.6,64.2,16.6,
16.2,39.6,101.6,92.2,47.6,74.4,11.4,92.8,51.2,125.2,103.8,102.2,
12.4,55,92.8,75.8,28.6,32.6,86,94.4,110.8,154.6,69.4,175.4,
61.2,108,54,15,101,12,29.4,100.2,33.2,31.4,65.4,60.4,
102.2,96.6,68,172.2,66.8,67,87.6,23.2,18.6,88,38.8,103,
127.4,75.8,50.8,84.8,1.4,80,9.4,131.4,84.8,110.4,126.6,108,
50.2,20.4,125.8,34,102.6,66.6,22.8,13,1,142.4,182.2,79.8,
64.2,25.6,85.2,74.4,31.4,13.4,45,15.8,99.8,172.2,1.6,152.2,
33,40.8,64.2,23.2,55.6,34.4,3.4,59.4,70.4,142.6,210.4,100,
23,199.6,128,65.6,22.8,34.2,8,192,12.4,73.2,17.6,37,
72.4,65.6,83.8,91.4,161,87.2,3.3,131.4,91,139.6,142.8,86,
93.8,67.6,147.2,9.2,94.4,25,15,72.2,0.4,58,117.8,32.6,
102.4,113.4,125.6,122,1.4,121.8,70,7.4,26.8,13,63.6,53.2)

Comunque lo sviluppo a partire da questo vettore verrà inserito in links  successivi.  Al termine aggiungeremo anche l’outputs senza errori come garanzia del lavoro

dataset_piogge_volt_24_5_-stag1_stag2_out_ok1 (1)

dataset_piogge_volt_24_5_-stag1_stag2_out (1)

Seguono i 5 grafici del link precedente a quello sopra, costruiti nell’ OUTPUT relativo. Dovremo aggiungere anche altri tre grafici  relativi all’output del nuovo ultimo links.

Nella serie dataset  ipotizziamo che sia assente un trend, come suggerito dal GRAF.1

I links successivi riguarderanno la Stagionalità, Fattori stagionali, Effetti stagionali.

_______________________________________________

Prove statistiche  e tentativi su ipotesi al fine di costruire un modello trasferibile.

#Ipotizzo che con una media mobile a tre termini pesata, #possa eliminare in buona parte i randoms da questa strana #serie dataset2 (già senza il trend come dal grafico).

yt2=dataset2; n2=length(yt2); mbt2=c()
for(t in 2: n2-1){mbt2[t]=(yt2[t-1]+2*yt2[t]+yt2[t+1])/4}
ts.plot(mbt2)

#Ho smussato dall’originale (dataset2 )i randoms per cui avrei ottenuto
#una serie senza i randoms (con plausibili stagionalità+ciclo; assente il trend
#iniziale come si vedeva ad occhio dal grafico di dataset2.
#Così se applico una media mobile di ordine dodici a mbt2 (primo caso), mi aspetto di trovare una serie con solo il ciclo.
#Potevo applicare la media mobile 12 direttamente su dataset2, smussandola
#di stagionalità e forse anche di randoms, e poi, togliendo
#la stagionalità+ randoms (questa nuova serie) da dataset2 avrei ottenuto solo
# il ciclo, perché all’inizio non possedeva trend .
#Protocollo sperimentale per  il modello: da confrontare questi due processi che dovrebbero condurre ambedue al ciclo.

#Questa serie con solo il ciclo la chiamo mbt2_12.

#PROVIAMO IL CASO 1:
yt=mbt2; n1=length(mbt2)-2; mbt2_12=c()
for(t in 7: n1-6){mbt2_12[t]=(yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+
yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+yt[t+6]/2)/12}

ts.plot(mbt2)
#stagionalità + randoms
lines(mbt2_12)

#CICLO; è la serie mbt2 smussata della stagionalità
#se tolgo stagionalità + ciclo – ciclo, mbt2-mbt2_12, ottengo la stagionalità.

#Stiamo pensando anche di scrivere direttamente i 372 valori

#della di X.2[4:375], nella variabile dataset2 con

#dataset2=c(………)

LA VERSIONE CORRETTA + I RELATIVI  CINQUE GRAFICsetwd(“F:/”)

dataset=read.csv("PIOGVOLTR0.CSV", header=T, dec=",", sep=";")

#Da osservare l'attributo dec=","! nell'argomento della funzione "read.csv".
 
#COME SI COSTRUISCE IL FILE PIOGVONTR.CSV a partire da foglio 1 di Excel.
 
par(ask=T) 
attach(dataset) 
X.1 
#Stampa i 372 dati della 1a colonna delle 7 colonne del DATA.FRAME 
#contenuto nel file PIOGVOLTR0.CSV (indicazione degli anni a partire dal 1956 
#intervallati da NA head(dataset) # X.1 X.2 X.3 X.4 X.5 X.6 X.7 
#1 1956 89,2 -3,3 70,62580645 #2 NA 32 2,0 73,94193548 #3 NA 68 10,2 83,02258065 
#4 NA 106 -2,0 72,30322581 #5 NA 39,8 -9,6 62,67741935 #6 NA 69,4 -21,0 52,52903226 
#Stampa i valori delle prime sei righe del data.frame, costituito da 
#sette colonne. 
X.2[4:375] 
#Stampa i 372 dati della 2a colonna in mm di pioggia mensili 
#partendo dall'anno 1956 con gennaio  
X.2[1:6] 
#Stampa i primi sei valori della seconda colonna 
#[1] 89,2 32 68 106 39,8 69,4
dataset=ts(dataset) 
#considera il data.frame dataset come una serie storica dataset2=X.2[1:372] 
#prende 1 valori da 1 a 372 del vettore X.2 e li mette 
#nella variabile dataset2 
dataset2=ts(dataset2) 
#dataset2 è una serie storica ts.plot(dataset2) 
#GRAF.1 #Stampa la serie storica dataset2; sembra assente il trend. yt2=dataset2; n2=length(yt2); mbt2=c() 
for(t in 2: n2-1){mbt2[t]=(yt2[t-1]+2*yt2[t]+yt2[t+1])/4} 
ts.plot(mbt2)
# GRAF.2 
#disegno il grafico di mbt2, GRAF.2, cioè i dati originali (senza trend) 
#privati anche dei random s.l.

GRAF.2
 
#Penso di smussare cioè dataset2 dai randoms s.l.; nel vettore mbt2 è plausibile 
#siano contenuti dati relativi a stagionalità e ciclo. 
#Ho smussato dall'originale (dataset2 )i randoms s.l. per cui avrei ottenuto 
#una serie senza i randoms (con plausibili stagionalità+ciclo); assente il trend 
#iniziale come si vedeva ad occhio dal grafico di dataset2. 
#Così se applico una media mobile di ordine dodici a mbt2 mi aspetto di trovare 
#una serie con solo il ciclo (PRIMO CASO). 
#Potevo applicare la media mobile 12 direttamente su dataset2 (SECONDO CASO), 
#smussandola dalla stagionalità e forse anche dai randoms (?), e poi, togliendo 
#la stagionalità + randoms (questa nuova serie) da dataset2 avrei ottenuto solo 
# il ciclo. 
#Da confrontare questi due processi che dovrebbero condurre ambedue al ciclo. 
#Questa seconda serie con solo il ciclo la chiamo mbt2_12. 
#PROVIAMO IL PRIMO CASO (applico una media modile 12 su mbt2: 
yt=mbt2; n1=length(mbt2)-2; mbt2_12=c() 
for(t in 7: n1-6){mbt2_12[t]=(yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+ yt[t-1]+
yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+yt[t+6]/2)/12} 
ts.plot(mbt2_12)
#GRAF.3 Disegno il grafico del ciclo

#GRAF.3
 

ts.plot(mbt2) # + CICLO1 sovrapposto. 
#Disegno il grafico di mbt2 (stagionalità + ciclo) e sovrappongo mbt2_12 (ciclo): 
lines(mbt2_12) 
#è la serie mbt2 smussata della stagionalità 
#Insieme al grafico mbt2 (stagionalità+ciclo) sovrappongo il ciclo: GRAF.4 #Se tolgo il ciclo da stagionalità + ciclo (mbt2), ottengo mbt2-mbt2_12, 
#cioè la stagionalità. 
#Sorge il problema che mbt2 e mbt2_12 debbono avere la stessa lunghezza

#per poterli sottrarre 
#FACCIO DELLE PROVE PER RENDERE I VETTORI LUNGHI UGUALE 
#Controllo mbt2 
length(mbt2) # 371 = 12 
head(mbt2) # NA 1.00 70.75 177.50 202.75 159.00 
mbt2=mbt2[2:(length(mbt2)-1)] 
#Controllo mbt2_12 
length(mbt2_12) # 363 
head(mbt2_12) 
# NA NA NA NA NA NA 
#Impongo che mbt2 e mbt2_12 abbiano la stessa lunghezza per sottrarli 
mbt2_12=mbt2_12[7: (length(mbt2_12)-6)] 
length(mbt2_12) 

#Proviamo il SECONDO CASO (applico direttamente la Mb12 su dataset2) 
#per il calcolo del ciclo 
yt=dataset2; n1=length(dataset2); mbt2_12_0=c() 
for(t in 7: n1-6){mbt2_12_0[t]=(yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+ yt[t-1]+
yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+yt[t+6]/2)/12} 
ts.plot(mbt2_12_0) 
#Disegno il grafico del ciclo nel secondo modo: GRAF.5  #Da confrontare i due grafici del ciclo mbt2_12_0 e mbt2_12. 
#I due cicli praticamente coincidono. Ma nel secondo sono rimasti 
#più errori randoms (?), nel senso che la Mb12 sugli originali 
#praticamente elimina da essi solo la stagionalità. Per cui
#nella serie nuova rimarrà ciclo+randoms e se sottraggo 
#Ciclo+Randoms dall'originale (dataset2) otterrei 
#direttamente la Stagionalità. #Potremmo fare un test statistico per controllo. 
#CALCOLO DELLA STAGIONALITA' nel proseguo (SECONDA PARTE) 

___________________________________________ OUTPUTS di R 
> rm(list=ls(all=TRUE)) 
> setwd("F:/") 
> dataset=read.csv("PIOGVOLTR0.CSV", header=T, dec=",", sep=";") 
>#COME SI COSTRUISCE IL FILE PIOGVONTR.CSV a partire da foglio 1 di Excel 
> par(ask=T) 
> attach(dataset) 
>#The following objects are masked from dataset (pos = 3): 
>X.1, X.2, X.3, X.4, X.5, X.6, X.7  
> X.1 
[1] NA NA NA 1956 NA NA NA NA NA NA NA NA NA NA NA 
[16] 1957 NA NA NA NA NA NA NA NA NA NA NA 1958 NA NA 
[31] NA NA NA NA NA NA NA NA NA 1959 NA NA NA NA NA 
[46] NA NA NA NA NA NA 1960 NA NA NA NA NA NA NA NA 
[61] NA NA NA 1961 NA NA NA NA NA NA NA NA NA NA NA 
[76] 1962 NA NA NA NA NA NA NA NA NA NA NA 1963 NA NA 
[91] NA NA NA NA NA NA NA NA NA 1964 NA NA NA NA NA 
[106] NA NA NA NA NA NA 1965 NA NA NA NA NA NA NA NA 
[121] NA NA NA 1966 NA NA NA NA NA NA NA NA NA NA NA 
[136] 1967 NA NA NA NA NA NA NA NA NA NA NA 1968 NA NA 
[151] NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA 
[166] NA NA NA NA NA NA 1970 NA NA NA NA NA NA NA NA 
[181] NA NA NA 1971 NA NA NA NA NA NA NA NA NA NA NA 
[196] 1972 NA NA NA NA NA NA NA NA NA NA NA 1973 NA NA 
[211] NA NA NA NA NA NA NA NA NA 1974 NA NA NA NA NA 
[226] NA NA NA NA NA NA 1975 NA NA NA NA NA NA NA NA 
[241] NA NA NA 1976 NA NA NA NA NA NA NA NA NA NA NA 
[256] 1977 NA NA NA NA NA NA NA NA NA NA NA 1978 NA NA 
[271] NA NA NA NA NA NA NA NA NA 1979 NA NA NA NA NA 
[286] NA NA NA NA NA NA 1980 NA NA NA NA NA NA NA NA 
[301] NA NA NA 1981 NA NA NA NA NA NA NA NA NA NA NA 
[316] 1982 NA NA NA NA NA NA NA NA NA NA NA 1983 NA NA 
[331] NA NA NA NA NA NA NA NA NA 1984 NA NA NA NA NA 
[346] NA NA NA NA NA NA 1985 NA NA NA NA NA NA NA NA 
[361] NA NA NA 1986 NA NA NA NA NA NA NA NA NA NA NA 
> #Stampa i 372 dati della 1a colonna delle 7 colonne del DATA.FRAME 
> #contenuto nel file PIOGVOLTR0.CSV (indicazione degli anni a partire dal 1956 
> #intervallati da NA 
>  head(dataset) X.1 X.2 X.3 X.4 X.5 X.6 X.7 
1 NA NA NA NA NA NA NA 
2 NA NA NA NA NA NA NA 
3 NA NA NA NA NA NA NA 
4 1956 89.2 NA NA NA -3.3 70.62581 
5 NA 32.0 NA NA NA 2.0 73.94194 
6 NA 68.0 NA NA NA 10.2 83.02258 
> # X.1 X.2 X.3 X.4 X.5 X.6 X.7 
> #1 1956 89,2 -3,3 70,62580645 
> #2 NA 32 2,0 73,94193548 > 
>#3 NA 68 10,2 83,02258065 
> #4 NA 106 -2,0 72,30322581 
> #5 NA 39,8 -9,6 62,67741935 
> #6 NA 69,4 -21,0 52,52903226 
> #Stampa i valori delle prime sei righe del data.frame, costituito da 
> #sette colonne. 
> X.2[4:375] 
[1] 89.2 32.0 68.0 106.0 39.8 69.4 33.4 25.2 64.4 41.4 123.8 34.4 
[13] 66.8 100.2 17.0 109.8 159.8 23.6 27.0 5.6 2.4 74.2 100.8 79.0 
[25] 47.4 27.0 133.0 108.8 36.0 30.6 22.0 21.0 12.8 163.8 67.0 134.4 
[37] 61.2 35.6 133.2 69.2 120.8 25.4 4.6 46.0 46.2 74.6 73.4 149.2 
[49] 57.8 112.8 113.4 62.0 9.6 91.4 64.6 5.2 179.6 214.6 132.2 210.2 
[61] 107.8 30.0 0.6 152.8 37.6 73.0 18.4 1.5 87.6 160.4 135.8 86.4 
[73] 50.4 46.6 139.6 35.6 35.6 21.6 37.6 50.0 64.8 161.6 196.8 35.4 
[85] 147.6 89.4 75.3 74.2 45.8 89.2 28.8 38.8 94.6 95.2 100.4 88.8 
[97] 4.6 77.6 157.6 58.8 49.6 32.2 84.0 69.5 34.0 193.0 78.0 118.4 
[109] 127.8 16.8 91.0 107.4 50.4 36.0 80.0 24.8 119.8 2.6 240.2 104.8 
[121] 97.8 88.4 28.4 28.4 36.2 28.6 67.2 52.2 122.8 173.4 259.0 59.6 
[133] 49.2 42.2 56.4 11.4 84.2 83.6 19.4 75.8 99.2 42.8 99.8 62.6 
[145] 57.0 149.8 29.8 49.0 156.0 91.4 28.0 65.8 35.6 75.0 148.2 68.0 
[157] 89.0 156.2 85.8 40.0 56.6 43.4 38.4 83.8 128.6 26.4 157.2 106.4 
[169] 104.8 98.2 140.6 79.6 66.6 63.8 18.6 22.4 75.0 28.2 106.4 95.0 
[181] 81.0 51.4 55.0 53.0 122.4 67.2 15.8 2.2 54.8 17.4 149.0 8.6 
[193] 85.4 91.8 43.0 106.8 51.4 26.0 71.0 49.0 136.6 76.0 46.8 67.2 
[205] 70.8 33.0 13.0 48.2 17.2 56.2 38.8 22.6 171.0 80.0 73.2 30.6 
[217] 35.4 105.2 66.0 80.6 52.8 27.2 12.6 61.4 88.8 87.6 64.2 16.6 
[229] 16.2 39.6 101.6 92.2 47.6 74.4 11.4 92.8 51.2 125.2 103.8 102.2 
[241] 12.4 55.0 92.8 75.8 28.6 32.6 86.0 94.4 110.8 154.6 69.4 175.4 
[253] 61.2 108.0 54.0 15.0 101.0 12.0 29.4 100.2 33.2 31.4 65.4 60.4 
[265] 102.2 96.6 68.0 172.2 66.8 67.0 87.6 23.2 18.6 88.0 38.8 103.0 
[277] 127.4 75.8 50.8 84.8 1.4 80.0 9.4 131.4 84.8 110.4 126.6 108.0 
[289] 50.2 20.4 125.8 34.0 102.6 66.6 22.8 13.0 1.0 142.4 182.2 79.8 
[301] 64.2 25.6 85.2 74.4 31.4 13.4 45.0 15.8 99.8 172.2 1.6 152.2 
[313] 33.0 40.8 64.2 23.2 55.6 34.4 3.4 59.4 70.4 142.6 210.4 100.0 
[325] 23.0 199.6 128.0 65.6 22.8 34.2 8.0 192.0 12.4 73.2 17.6 37.0 
[337] 72.4 65.6 83.8 91.4 161.0 87.2 3.3 131.4 91.0 139.6 142.8 86.0 
[349] 93.8 67.6 147.2 9.2 94.4 25.0 15.0 72.2 0.4 58.0 117.8 32.6 
[361] 102.4 113.4 125.6 122.0 1.4 121.8 70.0 7.4 26.8 13.0 63.6 53.2 
> #Stampa i 372 dati della 2a colonna in mm di pioggia mensili > #partendo dall'anno 1956 con gennaio (i dati del data.frame > #partivano da tre mesi prima (da ottobre 1955) > > X.2[1:6] [1] NA NA NA 89.2 32.0 68.0 > #Stampa i primi sei valori della seconda colonna > #[1] 89,2 32 68 106 39,8 69,4 > X.2=as.number(X.2) Errore: non trovo la funzione "as.number" > > dataset=ts(dataset) > #considera il data.frame dataset come una serie storica > > dataset2=X.2[1:372] > #prende 1 valori da 1 a 372 del vettore X.2 e li mette > #nella variabile dataset2 > > dataset2=ts(dataset2) > #dataset2 è una serie storica > > ts.plot(dataset2) #GRAF.1 Aspetto per confermare cambio pagina... > #Stampa la serie storica dataset2; sembra assente il trend. > yt2=dataset2; n2=length(yt2); mbt2=c() 
> for(t in 2: n2-1){mbt2[t]=(yt2[t-1]+2*yt2[t]+yt2[t+1])/4} > > ts.plot(mbt2)# GRAF.2 Aspetto per confermare cambio pagina... > #disegno il grafico di mbt2, cioè i dati originali (senza trend) > #privati anche dei random s.l. > #Penso di smussare cioè dataset2 dai randoms s.l.; nel vettore mbt2 è plausibile > #siano contenuti dati relativi a stagionalità e ciclo.  > #Ho smussato dall'originale (dataset2 )i randoms s.l. per cui avrei ottenuto > #una serie senza i randoms (con plausibili stagionalità+ciclo; assente il trend > #iniziale come si vedeva ad occhio dal grafico di dataset2. > #Così se applico una media mobile di ordine dodici a mbt2 mi aspetto di trovare > #una serie con solo il ciclo (PRIMO CASO). > > #Potevo applicare la media mobile 12 direttamente su dataset2 (SECONDO CASO), > #smussandola dalla stagionalità e forse anche dai randoms, e poi, togliendo > #la stagionalità + randoms (questa nuova serie) da dataset2 avrei ottenuto solo > # il ciclo. > #Da confrontare questi due processi che dovrebbero condurre ambedue al ciclo. > > #Questa serie con solo il ciclo la chiamo mbt2_12. > > #PROVIAMO IL PRIMO CASO (applico una media modile 12 su mbt2: > yt=mbt2; n1=length(mbt2)-2; mbt2_12=c() > for(t in 7: n1-6){mbt2_12[t]=(yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+ + yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+yt[t+6]/2)/12} > > ts.plot(mbt2_12)#GRAF.3 Aspetto per confermare cambio pagina... > Disegno il grafico del ciclo Errore: unexpected symbol in "Disegno il"  > ts.plot(mbt2) Aspetto per confermare cambio pagina... > #Disegno il grafico di mbt2 (stagionalità + ciclo) e sovrappongo mbt2_12 (ciclo): > lines(mbt2_12) #è la serie mbt2 smussata della stagionalità > #Insieme al grafico mbt2 (stagianalità+ciclo) sovrappongo il ciclo: GRAF.4  > #Se tolgo il ciclo da stagionalità + ciclo (mbt2), ottengo mbt2-mbt2_12, > #cioè la stagionalità. > #Sorge il problema che mbt2 e mbt2_12 debbono avere la stessa lunghezza > #per poterli sottrarre > > #FACCIO DELLE PROVE PER RENDERE I VETTORI LUNGHI UGUALE > > #Controllo mbt2 > length(mbt2) [1] 371 > # 371 = 12 > head(mbt2) [1] NA NA NA NA 55.3 68.5 > # NA 1.00 70.75 177.50 202.75 159.00 > mbt2=mbt2[2:(length(mbt2)-1)] > > #Controllo mbt2_12 > length(mbt2_12) [1] 363 > # 363 > head(mbt2_12) [1] NA NA NA NA NA NA > # NA NA NA NA NA NA > #Impongo che mbt2 e mbt2_12 abbiano la stessa lunghezza per sottrarli > mbt2_12=mbt2_12[7: (length(mbt2_12)-6)] > length(mbt2_12) [1] 351 > > #Proviamo il SECONDO CASO (applico direttamente la Mb12 su dataset2) > #per il calcolo del ciclo > > yt=dataset2; n1=length(dataset2); mbt2_12_0=c() > for(t in 7: n1-6){mbt2_12_0[t]=(yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+ + yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+yt[t+6]/2)/12} > > ts.plot(mbt2_12_0) Aspetto per confermare cambio pagina... > #Disegno il grafico del ciclo nel secondo modo. > #Da confrontare i due grafici del ciclo mbt2_12_0 e mbt2_12. 
> #I due cicli praticamentte coincidono. nel secondo sembra siano rimasti più 
> #errori randoms. Potremmo fare un test statistico per controllare
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::




                    ANALISI CON EXCEL DELLE PIOGGE A VOLTERRA 1956-1961
                   post terminato molte decine di anni fa dA PIERO PISTOIA

DA CONTINUARE

piogge_volterra-1956-1961

RIFLESSIONI SU UN ESEMPIO DI ANALISI STATISTICA CON R: MM DI PIOGGIA CADUTI IN CIASCUN ANNO DAL 1907 AL 1990 NELLA ZONA DI LARDERELLO (POMARANCE, Pisa) ED ALTRO; precisazioni su Regressioni lineari, Intervalli di confidenza ed altro, oltre al modo più o meno ortodosso di procedere; del dott. Piero Pistoia

PREMESSA

Post in via di sviluppo; fase iniziale di un processo che si costruisce nell’andare.

CURRICULUM DI PIERO PISTOIA :

::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

piero-pistoia-curriculumok-1-80Download

Questi ‘racconti’ di Statistica applicata di fatto sono modelli che automatizzano percorsi nell’analisi dei dati.

R è un programma potente e gratuito, continuamente aggiornato in tempo reale nelle principali Università del mondo. Sono disponibili centinaia di manuali gratuiti e migliaia di packages per tutte le esigenze.

Per vedere gli outputs anche grafici,  le istruzioni (quando pronte girano!) possono essere riportate, con copia incolla, per es, prima sul Blocco Note o direttamente sulla console di R. Nel procedere potremmo anche decidere di alternare le istruzioni ai grafici (vedremo). Nota bene: prima di incollare in R, è necessario ripulire il piano di lavoro di R, premendo dal MENU MODIFICA ‘Pulisci console’ e poi dal MENU VARIE ‘Rimuovi tutti gli oggetti’

Questi primi dati di Larderello sono stati ripresi dalla “COMUNITA’  DI POMARANCE 1-1991” consegnati alla Redazione da Mauro Fanfani, allora Tecnico presso il laboratorio ENEL.

Quelli di Volterra furono forniti dal dott. Juri Bettini.

—————————————-

RIFLESSIONI SU UN ESEMPIO DI ANALISI STATISTICA CON R: MM DI PIOGGIA CADUTI IN OGNI ANNO DAL 1907 AL 1998 NELLA ZONA DI LARDERELLO (POMARANCE, Pisa). POSSIBILITA’ DI TRASFERIRE, CON POCHE MODIFICHE, IL PROCESSO SU ALTRE ANALOGHE SERIE STORICHE (Es., Volterra 1956-1986)

PRECISAZIONI SU REGRESSIONI LINEARI, MEDIE MOBILI, TESTS STATISTICI, INTERVALLI DI CONFIDENZA, FORECASTS ED ALTRO, OLTRE AL MODO PIU’ O MENO ORTODOSSO DI PROCEDERE.
dott. Piero Pistoia

 Versioni del lavoro

PIOGGE_ANN_FORECAST_20_1_7.45

PIOGGE_ANN_20_1_LAPREVISIONE_ore17.45

PIOGGE_ANN_OUTPUTS_19.10

Si evidenziano i  files richiamati e si copiano sulla console di R: iniziano automaticamente a girare; se incontrano un grafico si fermano in attesa di un tasto premuto o un click del mouse, permettendo di stampare o memorizzare il grafico stesso. Volendo possiamo anche con copia-incolla trasferire pezzi dell’articolo, per es., da un grafico all’altro. Infine è possibile ricopiare le istruzione direttamente sulla console di R.

——————————-

PARTE PRIMA CON INSERIMENTO DI OTTO PAGINE DI GRAFICI (FIG. 1-8) RIPRESI DAGLI OUTPUTS

Si ‘guarda’ dentro i dati ‘provocandoli’ con le istruzioni di R!

#ESEMPIO DI ANALISI STATISTICA CON IL LINGUAGGIO R: MILLIMETRI
#DI PIOGGIA CADUTI IN CIASCUN ANNO DAL 1907 Al 1990
#A LARDERELLO E DAL 1956 AL 1986 A VOLTERRA.
#PRECISAZIONI SU INTERVALLI DI CONFIDENZA ED ALTRA STATISTICA
#dott. Piero Pistoia
#IN QUESTO PRIMO INTERVENTO SI PROPONGONO UNA SERIE DI AZIONI
#MESSE IN ATTO PER PORRE PUNTI INTERROGATIVI AI DATI
#DA ANALIZZARE. NEI GRAFICI SI ‘LEGGONO’ LE RISPOSTE RESE DAI DATI.

#I dati originali erano a scansione mensile, ma noi inizieremo
#ad analizzare i dati annuali ottenuti sommando i 12
#valori mensili delle piogge per ogni anno.

#Se volessimo esprime un’ipotesi sulla pioggia caduta nell’anno
#in un certo intervallo di anni, quella più immediata
#è che la quantità di essa costruisca nel tempo una serie
#stazionaria, senza uniformità interne, (assenza di trend,
#fluttuazioni di circa uguale ampiezza) perché sosterremmo
#che sommare le entità mensili ridurrebbe le oscillazioni
#stagionali di tutti i livelli, mentre non è così immediato
#pensare a fenomeni atmosferici e/o astronomici che
#possano attivare oscillazioni annuali periodi o non periodiche
#(come, per es. i cicli undecennali delle macchie solari…)

library(“UsingR”); library(“TTR”);library(“tseries”);
library(“graphics”);library(“forecast”)
#Le librerie, se non esistono già nella biblioteca attuale della
#versione, devono essere prima caricate dal Menù.

par(ask=T)
par(mfrow=c(2,2))

#Da prove preliminari si evidenzia che nella serie originale di
#Larderello esistono almeno tre autliers: nel 1913
#(636 sostituito da 736.2), nel 1915 (1505.5 sostituito
#da 1145) e 1972 (539.2 sostituito da 739.2), pensando ad una
#serie più armonica internamente (gli autliers, essendo ‘accideni’
#isolati pesano meno nel forecast).

#Con pochi cambiamenti possiamo analizzare meccanicamente diverse
#serie storiche fornendo il vettore dati:
#proponiamo la serie di Larderello di 84 dato a partire dal 1907
#e quella di Volterra di 30 dati a partire dal 1956

#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

Piogge_annuali_1907_1990=

c(1174,915.7,1204.1,1203.6,891.5,950.6,836.2, 960.6,1145.5,
1142.2,1156.3,876.4,1045.9,968.0,750.8, 878.3,
719.5, 720.7, 1045.7,1198.1,904.2,1142.0,958.0,
914.4,952.1,1141.8,1023.1,966.6,1013.0,823.1,1138.1,
763.1,1102,1083.0,949.3,1054.2,741.2,804.9,814.8,964.6,
1236.2,829.6,1086.2,782.9,1153.8,877.8,780.4,799.4,800.7,
863.8,760.7,821.6,753,1175.6,873,857.4,1192.6,1276.4,
1117.3,1251.2,742.4,1023.8,1107.4,845.6, 769.4,739.2,
782.7,799.2,985.6,1163.4,826.0,880.4,1067.7,923.6,903.6,
856.6,855.6,1010.4,842.1,891.7,1061.8,783,739.3,1009.6)
#si chiude o si apre il vettore dati per analizzare un’altra serie

piogann907990=ts(Piogge_annuali_1907_1990) #si chiude per altro
#vettore dati dello stesso nome yt0
yt0=piogann907990 #si chiude o si apre
t=c(907:990)#si chiude o si apre
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
#Di seguito analizziamo la serie di Volterra di trenta dati dal 1956.
#Da prove precedenti consideriamo 2 autliers 1960 (1253)e 1984 (1156)
#interpolando con 1000 e 950 rispettivamente

#yt0=c(727,766,804,839,1000,892,866,968,957,1002,1042,727,954,1012,869,678,851,655,698,858,988,
#671,932,991,841,781,837,813,950,733,821) piogge annuali Volterra 1956-1986
#t=c(956-986) #si apre o si chiude
#yt0=ts(yt0) #si apre o si chiude

#Fig. 1 -> quattro grafici sulla stessa pagina: 1)(yt0,Time); 2)acf(yt0);
#3)hist(yt0); 4)punti dati e retta di regressione

#3)hist(yt0); 4)punti dati e retta di regressione

ts.plot(yt0)

#Osservando il grafico dei dati ad occhio ci turba notare un certa tendenza
#delle piogge a diminuire nel tempo,
#falsificando le aspettative se il fenomeno fosse corroborato.

acf(yt0)

hist(yt0)

#Osservando il grafico dei coefficienti di auto-correlazione h,
#sembra chiaramente che all’interno della serie
#non ci siano legami di causalità avvallando le aspettative.

#Applichiamo comunque un modello di regressione lineare semplice
#ai dati per un controllo.
# INIZIO DELL’ELABORAZIONE DEI DATI

# Si prova a cercare il package Using-R
#library(“UsingR”)
#library(“TTR”)

# Fitta i dati delle piogge col tempo in anni e fornisce gli autputs

t=c(1:length(yt0))
result=simple.lm(t,yt0)
summary(result)

#FIG. 2 -> #plot (result) fitta 4 grafici per l’analisi dei residui:

#1)Nel primo (Residual,fitted) si osserva la diffusione dei dati intorno
#alla linea y=0 e il trend che non è ovvio. 2)Nel secondo (Normal qqplot),
#i residui sono gaussiani se questo grafico segue da vicino la linea
#tratteggiata.

plot(result)
par(mfrow=c(1,1)) #da ora si plotta grafico per grafico.
fit=lm(yt0~t)
attributes(fit)
summary(fit)
fit$coefficients
fit$resid

#plot(lm(yt0~t))
pre=predict(fit)# valori sulla retta
pre # valori predetti

#FIG. 3 -> acf(pre)

acf(pre)
# Plotta i dati e la linea di regressione
ts.plot(yt0)
abline(fit)
#Opppure:plot(t,yt0); abline(result)
yt1=yt0-pre

#FIG. 4 -> nel piano cartesiano “yt0,time” viene disegnato l’intervallo
#di confidenza al 90% per la media. Ci sono due tipi di intervallo,
quello di ‘confidenza per la media’ e quello per la ‘predizione individuale’,
#naturalmente più grande. Consideriamo questi intervalli al 90%. Nel secondo
#vengono riportati ambedue gli intervalli

# INTERVALLI DI CONFIDENZA
#1
summary(fit)
#2
predict(fit,data.frame(t=sort(t)),level=.90, interval=”confidence”)
#3
ci.lwr=predict(fit,data.frame(t=sort(t)),level=.90,interval=”confidence”)[,2]
#4
points(sort(t),ci.lwr,type=”l”)
#5
ci.upr=predict(fit,data.frame(t=t),level=.90, interval=”confidence”,add=T)[,3]
#6
points(sort(t),ci.upr,type=”l”)

#FIG. 5 -> punti-dati con i due intervalli, di confidenza e di previsone, al 90%

# Si possono usare comandi di più alto livello del package UsingR di VENABLE
fit=simple.lm(t,yt0)
summary(fit)
simple.lm(t,yt0,show.ci=T,conf.level=0.90,pred=T) #fa un po’ casino!

#FACCIO DELLE PROVE DI ‘SMUSSAMENTO’

#Elimino una parte del contenuto dei files piogann908990
# (yt0) con una media mobile di ordine 5, pesata con 1,2,3,2,1 (Media Mobile 3*3)
#con comandi di basso livello e osservo quello che accade
#(confrontare con media  mobile semplice 5)
#—————————

#SMUSSO5 pesato 1,2,3,2,1 (3*3)
m5=c()
for(i in 2:length(yt0)){
m5[i] =(yt0[i-2] +2* yt0[i-1] + 3*yt0[i] +2* yt0[i+1] + yt0[i+2])/9}
#prova a plottare m5
m5=ts(m5)
m5 # smusso5 la yt0 3*3; elimino dall’originale ciò che non è random!?

L’idea era solo sperimentare en passant, smussando con m5!

Da notare è che d’improvviso ho trovato cancellati i pesi dell’m5,                                                                           sbilanciando risultati e grafici!!

#——————————
#Secondo ‘pezzo’ per cambiare vettore dati da sottoporre al prog.
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

#Attenzione! devo fare modifiche per scegliere fra i due vettori dati
#da analizzare
m5=m5[3:82] #per Volterra (31 dati) va da 3 a 29; PER LARDERELLO (84 DATI)
#DA 3 A 82
n5=length(m5)
yt=yt0[3:82] #in yt ci sono da 3 a 82 dati yt<yt0; per Volterra 3-29
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

par=(mfrow=c(2,2))

yt
nyt=length(yt)
nyt
par(mfrow=c(2,2))

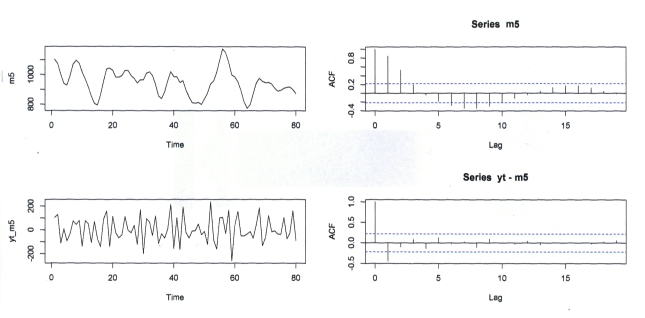
ts.plot(m5)
acf(m5)

yt_m5=yt-m5 #m5 e yt hanno la stessa lunghezza per cui si possono sottrarre
yt_m5 #originale meno m5_smussata

ts.plot(yt_m5)
lines(m5)

acf(yt-m5) # auto-correlazione di yt-smussamento 3*3

#Analizzo il vettore dati yt-m5 cercando la retta di regressione
t1=c(1:length(m5))
fit1=lm(yt_m5~t1)
summary(fit1)

La retta di regressione non esiste!

#FACCIO DELLE PROVE DI ‘SMUSSAMENTO’

——————————————————

# FIG. 6 -> 4 grafici sulla stesso piano: 1)graf. m5 (smusso 5 pesato 12321,3*3);
# 2)acf(m5); 3)graf. yt1=yt-m5 (yt è yt0 di lunghezza pari a m5 per sottrarre);
# 4)acf(yt1).

OSSERVAZIONI FUORI NORMA

Da osservare l’acf della serie yt-m5 : il picco fuori range può essere considerato dovuto a un caso accidentale come 1 su 20? e le oscillazioni smorzate dell’ acf di m5 non suggeriscono niente? Le armoniche di Fourier potrebbero ‘suonare’ qualcosa? Ritengo che non siano fuori luogo (anche se azzardate e deboli, ma cariche di significati scientifici, K. Popper,  ipotesi ‘tentative’ o Tentative Theory) su oscillazioni super-annuali  (di periodo circa 5, 11..?) relative ad armoniche rilevanti (si controllino anche i grafici di Fig. 7)

_________________________________

#TENTATIVI DI SMUSSAMENTO con SMA per raccogliere informazioni su                                                        #eventuali cicli super-annuali spesso periodici da analizzare con Fourier

piog3=SMA(yt0,n=3) #opero un semplice smussamento di ordine 3
piog5=SMA(yt0,n=5) # opero ora un semplice smussamento di ordine 5
piog8=SMA(yt0,n=8)
#piog11=SMA(yt0,n=11)
piog12=SMA(yt0,n=12) #opero un semplice smussamento di ordine 12
#piog15=SMA(yt0,n=15)

#ts.plot(piog3)
#ts.plot(piog5)
#ts.plot(piog8)
#ts.plot(piog12)

#smussa l’originale yt0 con 4 ordini (5 pesato 12312; 5;8;12)
par(mfrow=c(2,2))

#4 risultati dello smussamento di yt0: m5, 5, 8, 12

#FIG. 7 -> 4 grafici di smussamento sulla stessa pagina: 1)yt0 smussato m5;
#2)yt0 smussato 5; 3)yt0 smussato 8; 4)yt0 smussato 12.

ts.plot(yt0)
lines(m5,col=”orange”,lwd=2)
ts.plot(yt0)
lines(piog5,col=”orange”,lwd=2)
ts.plot(yt0)
lines(piog8,col=”blue”,lwd=2)
ts.plot(yt0)
lines(piog12,col=”red”,lwd=4)

#Osservando le ‘lisciature’ della curva_dati originale, sarebbe

#interessante sottoporre i vettori dati degli #smussamenti alla

#funzione del PERIODOGRAMMA (scritta dal dott. PIERO PISTOIA

#e testata e riportata nei diversi posts relativi ad esempi statistici a

#cura dello stesso scrivente: in particolare vedere “UN PARZIALE

#PERCORSO DI BASE SULL’ANALISI DI UNA SERIE STORICA

#REALE” dove tale funzione in .jpg è trasferibile e funzionante);

# per la ricerca di armoniche rilevanti.

#Non sembra così strano pensare ad influenze, per lo più

#periodiche,  del Cosmo esterno sulla nostra atmosfera, con periodi

#maggiori di un anno terrestre. Anche l’Analisi di Fourier  scritta

#col Mathematica di Wolfram, in più occasioni utilizzata dallo

#stesso autore, potrebbe essere uno strumento di controllo efficace.

#Si potrebbe anche riportare la Funzione _Periodogramma

#direttamente su questo post, per ogni possibile, anche futuro,

#utilizzo su qualsiasi vettore_dati.

par(mfrow=c(1,1))

#FIG. 8 -> 4 grafici di smussamento sullo stesso piano cartesiano (yt0,Time)

#Confronto 6 curve in un unico grafico (yt0,pre,m5,piog5,piog8,piog12)
ts.plot(yt0)
lines(pre)
lines(m5,col=”orange”,lwd=2)
lines(piog5,col=4,lwd=2)
lines(piog8,col=”blue”,lwd=2)
lines(piog12,col=”red”,lwd=4)
#Riflettiamo sullo smussamento interessante 12: sembra che esso tolga cicli super-annuali
#da investigarne in qualche modo le armoniche con fourier
# LA STATISTICA DI DURBIN WATSON

library(tseries)
y=yt0
n=length(y)
result=c()
result1=c()
for(t in 2:n){
result[t]=(y[t]-y[t-1])^2
}
result=result[2:n]
a=sum(result)
for(t in 1:n)
result1[t]=y[t]
b=sum(y)
dw=a/b
dw

#Possiamo usare anche funzioni di più alto livello caricando qualche #libreria nuova

#(‘lmtest’; attenzione alla versione di R!)

#PARTE SECONDA E IL PACKAGE ‘forecast’; si aggiungono
#6 pagine di grafici ripresi dagli outputs relativi

#Ci permettiamo di prendere un momento di riflessione in questo
#scorcio iniziale della PARTE SECONDA del nostro lavoro di
#’lettura’ dei dati. La retta di regressione apparsa ad occhio sui dati,
#dopo la regressione con i minimi quadrati di fatto ‘spiega’ ben poco
#del nostro campione (R-quadro trascurabile), ma se consideriamo
#le ‘statistiche campionarie T’ relative ai suoi coefficienti e le
#inseriamo sulle ascisse delle rispettive distribuzioni di Student,
#conosciute sotto l’ipotesi nulla, ci accorgiamo che probabilmente
#quella retta ‘esiste anche nell’Universo di tutti i campioni riferiti
#alla nostra ricerca. Così,nonostante questa retta non così ovvia,
#riteniamo ipoteticamente che: “se eliminiamo dai dati originali
#yt0, i valori della retta (pre), yt1=yt0-pre, già e ‘ricondizioniamo’
#il campione aggiungendo la media dei valori (cioè la media di yt0
#o di pre), otteniamo un valore migliore dell’originale almeno per
#l’applicazione del nostro modello di forecast (Simple Exponential
#Smoothing), cioè si rispetterebbero meglio i criteri di applicazione
#(omogeneità delle fluttuazioni col tempo, assenza di correlazioni
#interne…insomma migliore Stazionarietà)”. Tale ipotesi verrebbe
#controllata a posteriori con l’analisi dei residui. Basterà attribuire i
#valori della variabile ‘campione-condizionato’ alla variabile
#originale yt0 e procedere a far girare il programma successivo di
#previsione( yt0=campione-condizionato). Tale prova la qualche                                                                                 #lettore, se vorrà.

#yt1 era il vettore dei dati originali (yt0) meno le ordinate della retta
#(pre)

Myt0=mean(yt0); Mpre=mean(pre); Myt1=mean(yt1)

Myt0

Mpre

Myt1

#Dal plot di yt1

#Possiamo notare dal plot di yt1 che esiste un livello costante
#situato in corrispondenza ad valore di zero per la media; le
#fluttuazioni sembrano rimanere grossolanamente costanti nel
#tempo. E’ possibile probabilmente considerare la serie stazionaria,
#per cui si può tentare di usare un modello addittivo e uno
#’Smoothing Esponenziale Semplice’ per il forecast, forse con
#maggiore ‘matching’ di prima. Naturalmente bisogna
#’ricondizionare’ yt1 (centrata intorno alla media zero) alla serie
#originale. Riteniamo di poterlo fare aggiungendo ai valori di yt1, la
#media dei valori predetti ovvero dei valori originali; procederemo
#poi al solito a controllare questa scelta dal risultato (rilevanza del
#forecast)

Mpre=mean(pre)

yt0_condizionato=yt1+Mpre

#plotto yt0_condizionato insieme a yt0

FIG. 9′

ts.plot(yt0)
lines(yt0_condizionato,col=”blue”,lwd=2)

#Pongo:

#yt0=yt0_condizionato #per immettere nel processo_forecast i dati
#da cui si è tolto  il trend rettilineo di dubbia rilevanza

#Noi però intanto riguardiamo il grafico originale yt0 da sottoporre,

#con A. Coghian, (A LITTLE BOOK OF R FOR TIME SERIES; release

#0.2), ad un processo di previsione.

ts.plot(yt0)

——————————————-

#PARTE SECONDA: LA PREVISIONE
#PREMESSA SUL ‘SIMPLE EXPONENTIAL SMOOTHING (SES)’
par(ask=T)
par(mfrow=c(1,1))

#Piogge_annuali_1907_1990=

c(1174,915.7,1204.1,1203.6,891.5,950.6,836.2, 960.6,1145.5,
1142.2,1156.3,876.4,1045.9,968.0,750.8, 878.3,
719.5, 720.7, 1045.7,1198.1,904.2,1142.0,958.0,
914.4,952.1,1141.8,1023.1,966.6,1013.0,823.1,1138.1,
763.1,1102,1083.0,949.3,1054.2,741.2,804.9,814.8,964.6,
1236.2,829.6,1086.2,782.9,1153.8,877.8,780.4,799.4,800.7,
863.8,760.7,821.6,753,1175.6,873,857.4,1192.6,1276.4,
1117.3,1251.2,742.4,1023.8,1107.4,845.6, 769.4,739.2,
782.7,799.2,985.6,1163.4,826.0,880.4,1067.7,923.6,903.6,
856.6,855.6,1010.4,842.1,891.7,1061.8,783,739.3,1009.6)
#Ridefiniamo yt0
#yt0= Piogge_annuali_1907_1990

#FIG. 9
#ts.plot(yt0)

#Le righe dei commenti associati al programma che segue devono essere
#scorciate (con cancelletti all’inizio) se vogliamo far girare il tutto dalla console di R!
#come accade nella prima parte di questo post; in caso contrario vanno riscritte le linee di programma
#in successione sulla console di R

#Il metodo del Semplice ‘Lisciare’ Esponenziale è raccomandato quando 1) i dati non
#presentano un trend ‘esplicito’ e, 2) non è coglibile una stagionalità.

#Da precisare che non si ha ‘trend esplicito’ anche quando si ha, sì, un cambiamento di livello
#o media nel corso del tempo fuori del random, ma tale evento si presenta poco regolare e
#intuibile, scarsamente razionalizzabile in un trend ‘esplicito’

#Sono almeno tre i possibili interventi nei processi di forecast del metodo SES , due
#praticamente immediati, il metodo ‘ingenuo’ , o ‘naive methods’, ‘average methods’
#(per prevedere è importante solo l’ultima osservazione che rimane costante nel tempo
#di previsione), l’altra, il metodo della ‘Media’ (i valori predetti sono tutti uguali alla media
#dei valori che servono per prevedere) e il terzo, più mediato, usa medie pesate, che tengono conto
#dei valori pesandoli in maniera diversa; quelli più lontani sempre meno di quelli più vicini
#secondo una curva esponenziale.

#Fra i modelli del terzo tipo utilizzeremo due modelli di HoltWinters con le funzioni di R HoltWinters()
#e forecast.HoltWinters(); per es., per Larderello: valori annuali 1907-1990; per Volterra valori
#annuali 1956-1986.

#RIASSUMIAMO IL PROCESSO

#Poiché riteniamo di avere una serie storica a cui si può applicare un modello addittivo con fluttuzioni
#pressochè costanti pressochè costanti e che possiede un livello che si mantiene, pensiamo, uguale
#nel tempo (valore medio) e nessuna stagionalità, possiamo usare uno dei tanti modelli SES (Simple
#Exponential Smoothing), per brevi previsioni future, cioè un mezzo per stimare i livelli previsti nei
#punti correnti col tempo.

#Se usiamo però un SES predittivo che utilizza la funzione HoltWinters() di R, sono necessari,
#per questo modello due parametri da immettere nell’argomento, beta e gamma che nella fattispecie
#dobbiamo uguagliare a FALSE (si cambia il loro valore, per es., per casi con trend e/o stagionalità),
#mentre calcola da sé il terzo parametro alfa, che controlla lo smoothing (alfa vicino a zero significa
#che diamo più peso ai dati recenti). Come outputs abbiamo il valore di alfa e tutti i valori previsti
#corrispondenti ai dati delle misurazioni originali (nella fattispecie 84) con cui è possibile costruire
#la curva di previsione all’interno dei dati.

#La funzione di HoltWinters() memorizza gli outputs in una lista di ‘oggetti’ da richiamare contenuta
#nella variabile ‘yt0previsti’ da noi scelta. Così la funzione HW() scrive i valori previsti (ed altro) in
#uno dela lista degli ‘oggetti’ (fitted, SSE…) contenuti nella variabile yt0previsti calcolata, per cui
#essi si troveranno nella variabile yt0previsti$fitted. Gli ‘errori della previsione’ si calcolano
#sottraendo dai valori predetti quelli osservati e l’oggetto SSE (Sum of Squared Errors),
#rappresenta una misura dell’accuratezza del forecast, fornito sempre dalla HW( ), che
# invece verrà richiamato da yt0previsti$SSE.

#E’ interessante notare che è necessario scegliere un valore iniziale di partenza per il calcolo
#dei livelli previsti; se questo valore non viene esplicitato il programma sceglie il primo valore
#dei dati.

#Ci sono anche dei processi per aiutarci a scegliere questo valore.

#Possiamo immettere però anche questo primo valore scelto da noi, aggiungendo il
#parametro ‘1.start’ nell’argomento della funzione HoltWinters(),

#HoltWinters(yt0, beta=FALSE, gamma=False, 1.start=X)

yt0previsti=HoltWinters(yt0,beta=FALSE, gamma= FALSE)
yt0previsti

#HoltWinters exponential smoothing without trend and without seasonal
#component.

yt0previsti$fitted

plot(yt0previsti)

FIG: 10

#La funzione HoltWinters() calcola i forecasts solo per i dati originali (nella
#fattispecie quelli da 1907 a 1990). Se vogliamo prevedere alcuni dati futuri
#(es., 8) è necessario scaricare il package di R ‘forecast’ , tramite library(‘forecast’),
#il quale contiene la funzione nuova ‘forecast.HoltWinters()’, che memorizzerà l’output
#nella variabile da noi scelta yt0previsti2 e aggiungeremo nel suo argomento
#’yt0previsti, h=8′
yt0previsti2 = forecast.HoltWinters(yt0previsti, h = 8)

#Con la funzione plot.forecast messa disposizione dalla libreria scaricata possiamo stampare
#le predizioni ottenute con la funzione forecast.HoltWinters():

plot.forecast (yt0previsti2)

#La funzione forecast.HoltWinters() dà la previsione per ogni anno con un intervallo di
#predizione all’80% (fascia arancionee) e al 95% (fascia gialla).

library(“forecast”)

FIG. 11

#La funzione HoltWinters() calcola i forecasts solo per i dati originali (nella
#fattispecie quelli da 1907 a 1990). Se vogliamo prevedere alcuni dati futuri
#(es., 8) è necessario scaricare il package di R ‘forecast’ , tramite library(‘forecast’),
#il quale contiene la funzione nuova ‘forecast.HoltWinters()’, che memorizzerà l’output
#nella variabile da noi scelta yt0previsti2 e aggiungeremo nel suo argomento
#’yt0previsti, h=8′
yt0previsti2 = forecast.HoltWinters(yt0previsti, h = 8)

#Con la funzione plot.forecast messa disposizione dalla libreria scaricata possiamo stampare
#le predizioni ottenute con la funzione forecast.HoltWinters():

plot.forecast (yt0previsti2)

#La funzione forecast.HoltWinters() dà la previsione per ogni anno con un intervallo di
#predizione all’80% (fascia arancionee) e al 95% (fascia gialla).

acf(yt0previsti2$residuals, lag.max=20)

FIG. 12

#Osservando l’acf dei residui può accadere che qualche ordinata superi la zona permessa
#(dove c’è assenza di autocorrelazione). Può essere che uno o due segmenti escano dai
#’significance bounds’. restando incerti se, fra 1-20 lags, ci sia qualche correlazione significativa.
#Per una conferma attiviamo il test in R di Ljung-Box-test che usa la funzione “ Box-test()”

#della libreria(stats):

#Box-test(yt0previsti2$residuals, lag=20, type=”Ljung-Box”)
#IL TEST DI LJUNG-BOX

#Se il p-value supera 0.05 di poco ci sarà una piccola certezza di qualche correlazione interna,
#che decideremo se sia dovuta al caso.

#E’ buona idea controllare anche la costanza della varianza e la normalità della distribuzione
#dei residui. Per la costanza della varianza facciamo il plot dei residui con il tempo.

plot.ts(yt0previsti2$residuals)

#Appare un grafico che presenta una successive di fluttuazioni col tempo. Può accadere a vista
#che in alcune parti del tempo l’ampiezza di esse risulti leggermente divers da quella di altre parti.
#Sarà da decidere se riteniamo che sia circa costante sostenendo l’ipotesi della uguaglianza
#della varianza col tempo

FIG: 13

#Per controllare infine se gli errori di previsione siano a distribuzione gaussiana con media zero,
#faremo in un istogramma (area coperta=1) degli errori con sovrapposta una curva gaussiana
#con media zero e deviazione standard pari a quella della distribuzione degli errori di previsione.
#Per far questo, di seguito viene riportata la routine di Avril Coghian di cui l’autore si sente debitore
#di questo scritto.

#Basta, dalla console di R, richiamare la funzione, scritta ad hoc, plotForecastErrors() con l’argomento
#’yt0previsti2$residuals’:

#INIZIO FUNZIONE PERSONALE
#plotForecastErrors=function(forecasterrors)

plotForecastErrors=function(forecasterrors)
{
#faccio un istogramma degli errori di previsioni

mybinsize=IQR(forecasterrors)/4
mysd=sd(forecasterrors)
mymin=min(forecasterrors)-mysd*5
mymax=max(forecasterrors)+mysd*3

#Genero una distribuzione di dati gaussiana con media zero e standard deviation
#pari a mysd

mynorm=rnorm(10000,mean=0, sd=mysd)
mymin2=min(mynorm)
mymax2=max(mynorm)

if (mymin2<mymin){mymin=mymin2}
if (mymax2>mymax){mymax=mymax2}

#Faccio un istogramma rosso degli errori di previsione con un gaussiana
#sovrapposta.

mybins=seq(mymin,mymax,mybinsize)
hist(forecasterrors, col=”red”, freq=FALSE,breaks=mybins)

#freq=F assicura che l’area sotto l’istogramma è = 1.
#genera una gaussian con media zero e standard deviation mysd

myhist = hist(mynorm,plot=FALSE, breaks=mybins)

#plotto una gaussiana blu sopra l’istogramma ddegli errori di previsione:

points(myhist$mids,myhist$density, type=”l”,col=”blue”,lwd=2)
}
#FINE FUNZIONE
plotForecastErrors(yt0previsti2$residuals )

#Possiamo usare questa funzione per costruire un istogramma con gaussiana
#degli errori di previsione per qualsiasi predizione delle
#piogge!
FIG. 14

e cambiando scala verticale:

#Da controllare se la distribuzione degli errori è grossolanamente centrata

#sullo zero, se è più o meno distribuita come una gaussiana, se è ‘skewed’
#da una parte rispetto alla curva normale, ecc.

#Comunque, a mio parere, è da sottolineare che questi nostri racconti di
#statistica nel loro articolarsi, non di rado si imbattono in scelte volontarie
#ed intuitive su grandezze in gioco e questo suggerisce che non è necessario
#poi in generale un atteggiamento troppo intransigente e restrittivo nelle
#valutazioni sulla rilevanza delle ipotesi.

——————————————-

40 916.8477 916.8477