NDC
Una breve poesia di A. Machado come intermezzo.
RIPROPONIAMO ALL’ATTENZIONE QUESTO ARTICOLO IN UN LINK PER ‘PERTURBARE’, TRAMITE I ‘SEMI’ DEL DUBBIO, IL PENSIERO DI MANICHEI E SICURI DI SE’, CHE ‘SPARATORI’ DI GIUDIZZI A VENTAGLIO DALLE LORO CERTEZZE, RISCHIANO DI NON VEDERE LONTANO.
Post in divenire……
In questo scritto, nato al tempo come una relazione didattica di auto-aggiornamento oggi rivisitata, furono trascurati i riferimenti bibliografici. Da controllare, precisare ed eventualmente da aggiungere (J. BRUNER, TORALDO di FRANCIA ed tanti altri)
OGGETTO ARTISTICO/OGGETTO REALE E OGGETTO ARTISTICO/OGGETTO FISICO
RIFLESSIONI DIFFORMI DI PIERO PISTOIA
Perché l’argomentazione difforme e provocatoria (a differenza di quella razionale anche di buon senso, che è capace di tracciare nel complesso, per es., due percorsi razionali incompatibili, cioè A + contorno può portare a Bianco, ma anche a Nero, giustificando tutto! ) possa facilitare almeno la consapevolezza della strana morale degli occidentali (sia quelli con grande Storia, sia quelli senza Storia, perché, forse, Historia magistra vitae è una falsa sentenza), brava gente di cuore, di intelletto e spesso timorosa di Dio insomma, che, nel migliore dei casi, sa offrire come una grande opera morale di carità il curare feriti a migliaia e il sotterrare morti a migliaia per lo più innocenti, colpiti ed uccisi proprio da loro! Spesso con l’educare al difforme e al provocatorio si può intravedere meglio la giusta via! Chi pensate vedrà prima la stretta asola nella trappola per mosche di Wittgenstein? Il difforme o il razionale di buon senso?
Accettiamo come postulato che l’oggetto poetico (artistico) e l’oggetto reale posseggano, per loro natura, ambedue infinite sfaccettature, infinite possibilità di significati razionali e/o irrazionali, ambedue non siano riducibili o coglibili fino in fondo. Gli ‘umani’ cambiano nel tempo insieme al loro background di interpretazione, ma Natura e Poesia rimangono e si pongono come un obbiettivo regolativo incompiuto….per sempre.
Postuliamo altresì che l’oggetto poetico (artistico) abbia un disordine intrinseco che si ‘attua’ in ‘vortici’ del linguaggio, come quello reale, pur nelle differenziazioni dei significati, un disordine ordinato in qualche modo, un caos con un suo ordine interno.
La comprensione dell’oggetto poetico è quindi solo parziale anche per lo stesso poeta, a differenza dell’oggetto fisico che, pur tendenzialmente in divenire, viene sempre compreso completamente ad ogni stadio, dallo scienziato che lo ‘costruisce’ (sull’oggetto fisico ci si fanno i conti, si costruiscono oggetti della tecnica e della tecnologia! Verum est factum di vichiana memoria). L’oggetto fisico, infatti, espresso da teorie, è razionalmente comprensibile fino in fondo ad ogni fase di sviluppo a differenza dell’oggetto reale. E’ vero che possono esistere infinite possibilità fisiche di vedere razionalmente l’oggetto reale, ma queste possibilità non saranno mai esprimibili in una teoria che abbia essa stessa infinite possibilità di interpretazione (che comunque sarebbero tutte razionali: infinità di ordine inferiore rispetto alle infinità della classe delle possibili interpretazioni dell’oggetto poetico e naturale).
L’oggetto poetico e dell’arte non è comprensibile né riducibile ad un processo razionale, né comunque esauribile da qualunque umano; la sua interpretazione non diverrà mai definitiva. Tutte le possibili interpretazioni razionali e tutte quelle emotive irrazionali o inesprimibili, coglibili solo nell’atto immediato dell’intuito, infiniti punti di vista come monadi leibniziane, sarebbero sezioni di un invariante poetico, l’oggetto poetico.
Possiamo allora concludere che l’oggetto poetico assomiglia (nel senso della complessità) di più all’oggetto reale di quanto somigli ad esso l’oggetto fisico.
Ne deriverebbe allora che l’oggetto reale, l’Alter Ego del soggetto, il noumeno kantiano, potrebbe essere compreso più in profondità se si utilizza, per la sua scoperta, l’oggetto poetico (od anche l’oggetto poetico) di quanto lo sia utilizzando l’oggetto fisico (o solo l’oggetto fisico)?
La risposta alla domanda formulata non è possibile se non vengono precisate le condizioni di costruzione dell’oggetto poetico e in cosa consiste l’oggetto fisico. Il coinvolgimento totale del soggetto nell’oggetto, escluderebbe la possibilità di cogliere l’esterno del soggetto stesso, ammesso che esista. Quindi questo oggetto complesso, risultato dell’atto poetico, sembra costituire una fusione quasi mistico-religiosa, del soggetto nell’oggetto, ad animare un oggetto di per sè non coglibile, a meno che non si voglia ammettere che le cose dell’Universo consistano di una congerie di materia e spirito (Heghel). Solo in tal caso l’oggetto poetico potrebbe corrispondere all’oggetto reale in quanto costituito della stessa sostanza ed ugualmente complessi. Questi due aspetti non garantiscono però un matching necessario, in quanto può accadere che nonostante ugualmente complessi e della stessa pasta abbiano struttura completamente diversa. E’ necessario ammettere ancora qualcosa.
Se quest’ultimo aspetto comunque fosse vero (presenza di matching), l’atto poetico sarebbe più efficace dell’atto scientifico a cogliere la realtà dell’Universo. Si verrebbe così a confermare la posizione di Vico che affermava come il noumeno potesse essere colto nell’attività mistica e artistica ed altre posizioni sostenute dalle religioni orientali. Se poi questo aspetto non risultasse vero, allora la suddetta proposizione dovrebbe essere presa come postulato di partenza per poter sostenere il matching.
E’ comunque da precisare che, anche se l’invariate poetico corrispondesse alla realtà, ciò non significa che tale oggetto possa essere compreso completamente nell’esperienza di un solo soggetto, sia esso l’artista od il fruitore.
La questione potrebbe essere però risolta in un altro modo. Ammettiamo che l’Universo consista di un oggetto estremamente complesso in cambiamento evolutivo (crescita? Ontogenesi? Filogenesi?); ogni parte di esso è istante per istante in equilibrio con tutte le altre a formare un tutt’uno strutturato finemente. La stessa vita porta traccia di questa struttura nel senso che ogni parte di questo insieme porta scritto in qualche modo informazioni relative al resto dell’Universo (per es., gli elementi chimici costituenti i nostri corpi sono stati prodotti nell’esplosione di super-nove!). Pur evolvendo ogni cosa che esiste, ad un certo stadio, già c’era in precedenza, anche se in qualche altro stato. La stessa mente o spirito deve (?) essere parte integrante di tutta la materia dell’Universo. Ma il ‘deve’ nell’ultima proposizione non può essere logicamente sostenuto. Se da una scatola chiusa esce un coniglio non è logicamente inferibile che un momento prima esso fosse dentro la scatola! Si pensi ad un elettrone che esce da un nucleo radioattivo nonostante che sia impossibile per un elettrone albergare in un nucleo! Ma al posto dell’elettrone nel nucleo c’è qualche altra cosa, per es., energia sotto forma di massa a costituire parte di un neutrone: ma è la stessa cosa? Una congerie di elementi diversi già esistenti a configurare un nuovo oggetto, è la stessa cosa dell’insieme non strutturato degli stessi elementi?
Ammettendo la validità del ‘deve’, qualsiasi atto creativo avrà a che fare con archetipi profondi legati a questa struttura dell’Universo, che, in quanto mente e corpo, è coglibile attraverso una riflessione umana. E’ possibile inoltre che l’uomo abbia formato un nodo estremamente denso di linee di struttura rispetto ad altri oggetti e quindi che i legami archetipici con l’Universo siano profondi e ricchi di informazioni.
Ma ad un certo stadio evolutivo l’equilibrio dovette cessare improvviso, come fu improvviso (in senso geologico) il salto qualitativo che condusse l’Homo sapiens all’Homo, che chiameremo, sapiens sotto-specie sapiens (indicando il passaggio fra un Homo con corteccia in via di trasformazione, in situazione lontana dall’equilibrio, ad uno con corteccia praticamente definitiva, come la nostra.
Non è del tutto inverosimile pensare che, data la tendenza degli svariati elementi costituenti gli organi, in particolare il cervello, a correlarsi fra loro, gli ultimi salti evolutivi, richiesti dall’uso sempre più consapevole della mano (teoria adattiva del Neo-darwinismo), abbiano trascinato nello sviluppo evolutivo una miriade di elementi cerebrali a costituire un cervello con possibilità enormi rispetto alle richieste iniziali (simile a quello che sarebbe accaduto per l’occhio estremamente complesso dei polpi). Ovvero le oscillazioni sempre più ampie intorno ad un centro lontano dall’equilibrio avrebbero condotto, in questa fase in particolare, ad un salto qualitativo non spiegabile con le richieste adattive (Teorie degli Equilibri Punteggiati).
L’inizio della mancanza di equilibrio con la Natura iniziò quando entrò in gioco la costruzione orientata ad una attività sempre più simbolica della corteccia e quindi l’inizio di un successivo indebolimento, in questo processo, della costruzione di archetipi legati all’azione della corteccia.
Allora, se la razionalità nella sua pienezza corrisponde a queste ultime conquiste evolutive, non è forse da chiederci se essa, certamente umana, sia davvero da considerarsi conforme alla Natura.
Si conclude: a) non ci fu più equilibrio completo da quando entrò in gioco la costruzione sempre più simbolica da parte della corteccia, aspetto del cervello non in equilibrio con la Natura; b) non si hanno archetipi legati all’azione della corteccia (?); c) l’oggetto creato dalla corteccia non è un oggetto naturale.
Così solo l’atto creativo può evocare dal profondo spinte archetipiche atte a costruire un oggetto complesso della stessa ‘pasta’ dell’Universo e ad esso corrispondente. Con l’intuizione estetica o mistica e la riflessione-meditazione filosofica profonda sembra così essere possibile raggiungere gli stessi obbiettivi della scienza ed oltre?
Si potrebbe evincere anche che l’Homo prima del sapiens, in perfetto equilibrio con l’Universo, potesse provare esperienze di fusione mistico-magico-creative con gli oggetti dell’Universo (Empatia? Einfunlung?) così profonde da poter cogliere la ‘Realtà’ in una sola esperienza personale ovvero in una esperienza condivisa all’unìsono (Telepatia?) dall’orda, esperienza catalizzata ed evocata dalla presenza dell’oggetto artistico (Neanderthal e pitture relative alla sua scultura).
Esistono così due modi di intervento sul mondo, uno guidato da teorie e modelli logici messi alla prova usando processi razionali quantitativi di controllo o suggeriti dalle teorie del complesso e l’altro procedendo lungo le direttrici suggerite dalle teorie del qualitativo. Non si tratta però né di due aspetti ugualmente radicati profondamente come archetipi nell’animo umano, rispettivamente correlati alle filosofie della causa e del fine (razionalismo e irrazionalismo, scientismo e umanesimo, mano destra e mano sinistra…), né da cercare di armonizzare e integrare. La situazione è ben diversa: tertium non datur.
I problemi che sorgono nell’interazione uomo-natura non si risolvono, o non si procede efficacemente nella loro soluzione, muovendoci, guidati da qualche teoria della conoscenza, dalla raccolta dei dati, attraverso la loro elaborazione, per intervenire a modificare la situazione teorica iniziale, a fronte di strumenti che non permetteranno mai di cogliere la realtà di interrelazione fra le cose. La soluzione si ottiene cambiando completamente tattica e atteggiamento.
I mondi della logica, della matematica, delle scienze positive e i correlati mondi del ragionamento razionale, delle argomentazioni critiche, degli standards universali, delle prescrizioni , delle tradizioni rigide…rappresentano una sezione artificiosa e riduttiva del complesso pensiero umano. Essi derivano da una riflessione parziale ed incompleta sui processi mentali atti a rispondere alle richieste della sopravvivenza e dell’istinto di conservazione.
Questi mondi costruiti dall’uomo che utilizzano tali processi riduttivi del pensiero, risultano solo parzialmente umani e stranamente separati dalla Natura (mondi artificiali costruiti dall’uomo su dati incompleti relativi al funzionamento del suo pensiero e quindi scarsamente agganciati all’equilibrio naturale). Ci siamo accorti infatti non solo che a) il pensiero intuitivo-creativo non è analizzabile in termini di scansioni veloci, automatiche e non consapevoli attraverso percorsi cibernetici, l’atto creativo rappresenta una visione immediata e orizzontale della soluzione a problemi, ma anche b) tutti gli altri processi del pensiero umano non seguono sempre e comunque i passi scanditi da un particolare software, atto al raggiungimento di un dato obbiettivo (non esiste necessariamente omologia fra pensiero e software).
Da questo consegue che le teorie scientifiche sono solo condizione necessarie ma non sufficienti (Toraldo di Francia) per cogliere la realtà ed il progresso della scienza si riduce solo all’adeguare funzionalmente (fitting) modelli e teorie all’ambiente sperimentato (Convenzionalismo?), nel senso della sola ricerca della semplicità, coerenza e capacità di spiegazione e previsione. Il fatto quindi che una chiave (teoria) apra una porta (risolva un problema), dalla chiave che apre non si evince niente sulle caratteristiche della porta (come da una chiave che non apre, teoria falsificata!).
Se una nave urta gli argini di un canale avvolto nella nebbia, dirò che il percorso non è adatto a descrivere la geometria del detto canale; se invece attraversa il canale (teoria non falsificata e quindi corroborata) non posso affermare che il percorso corrisponda (match) alla traccia del canale, perché la nave può aver percorso le più svariate linee, anche fortemente a rischio, che non hanno niente a che vedere con la “vera” forma del canale.
Il non adatto viene “falsificato” e quindi eliminato: niente però viene detto sulla “verosimiglianza” (termine di Popper), sulla corrispondenza ed omologia fra teoria ed ambiente reale (Popper è meno pessimista). Da una parte ciò conduce all’impossibilità di cogliere l’oggetto in sé , il noumeno kantiano, dall’altra alla realizzazione fattiva di opere e strutture sociali non in equilibrio né con l’uomo né con la Natura, conseguenza delle posizioni degli efficientisti, dei manichei coerenti e intransigenti, dei possessori di verità con in tasca le chiavi dei ghetti e delle camere a gas (tutti figli del razionalismo), che, insieme ai pazzi, sono e sono stati nella storia, vicina e lontana, i soli responsabili di efferati genocidi e di guerre inumane e ingiuste.
Il disagio che ne deriva ha condotto alle dualità espresse nelle distinzioni già nominate fra mano sinistra e mano destra, arte e scienza positiva, mondo dei valori e mondo della ragione… e ultimamente alla individuazione di particolari problemi detti ipercomplessi, le cui soluzioni non sono possibili con i soli strumenti della ragione.
In effetti tutti i problemi che riguardano l’Universo – in particolare quelli di natura sociale – sono, a mio parere, di natura ipercomplessa, la cui soluzione è resa possibile solo attraverso una riscoperta dei profondi legami fra ragione e non, coglibili nelle primitive operazioni mosse dall’istinto di conservazione e dagli altri archetipi collegati all’ambiente di sopravvivenza (caccia e raccolta), nel quale per più di due milioni di anni il cervello ha sviluppato le proprie caratteristiche profonde. Forse nello studio del pensiero-comportamento degli ominidi fino al Neandethal, cioè prima dei Cromagnon, potremmo trovare indizi di questo aspetto mancante e abbozzare così una risposta se mai esiste.
L’inesistenza di risposte a tali dicotomie dovrebbe allora essere ricercata forse nella incompletezza del cervello umano. In tal caso comunque dovrà esistere un controllo capillare delle costruzioni artificiali, siano esse opere o ragionamenti, da parte degli aspetti umani più primitivi, ma certamente più in equilibrio col Tutto.
Allora con gli ultimi salti evolutivi la capacità di costruire simboli e quindi teorie fornì un nuovo metodo di programmazione e manipolazione dell’ambiente per la sopravvivenza della specie ed oltre: un metodo certamente umano, perché posseduto dall’uomo, ma non naturale, in quanto non previsto dalle esigenze e dalla cultura (caccia e raccolta) in cui si era sviluppato il cervello umano in equilibrio col tutto.
Data l’efficienza e la soddisfazione conseguente a tali processi che facevano morire teorie al posto di organismi, questo metodo affascinò a tal punto che fu dimenticato quasi completamente l’altro. Ed era l’altro quello in equilibrio con l’Universo, quello del rispetto dell’essere vivente, dell’oggetto inanimato e dell’energia; quello del vivere sociale armonico e condiviso, anche se per piccoli gruppi.
Da quel momento le orde non si riunirono più intorno all’opera d’arte (per es., una preda) a meditare al fine di cogliere l’oggetto ‘reale’, il noumeno kantiano, per controllare il futuro (procurarsi ritualmente il cibo). Da quel momento quel metodo si ridusse in brandelli, i cui resti in tracce ancora oggi rimangono nebulosi nel profondo del nostro essere e quando riusciamo a prenderne consapevolezza si rimane invischiati in una dualità irrisolvibile. Dovevamo accorgerci da subito che l’altro, non vistoso, non luminoso ed immediato, era invece il metodo più potente, in quanto alla nostra sopravvivenza avrebbe partecipato il Tutto completamente compreso.
Molti scritti sacri delle più disparate religioni non suggeriscono forse di dimenticare la logica, la scienza e le loro opere? E le teorie, da queste discipline razionali proposte, non sono forse solo convenzioni, che funzionano sì (a guisa di protocolli applicativi), ma solo per i nostri scopi a danno di Tutto, e quindi anche di noi stessi?
Armonizzare ed integrare questi due aspetti è senza senso: con la mano destra invento costruzioni artificiali per lo più tautologiche e, forzando, le rendo funzionali ai miei scopi (Verum ipsum factum), con la mano sinistra riesco a costruire, ormai malamente, oggetti incompleti i cui significati operativi rimangono nebulosi; le loro potenzialità, nel migliore dei casi, rimangono imprigionate al di sotto di una semplice armonia estetica virtuale che ‘accarezza l’animo umano’, come l’oggetto artistico! Pur tuttavia, un grande oggetto umano è l’arte! ma, perché incompiuto, non riuscirà mai più a gestire operativamente in maniera diretta né il presente né il futuro (forse, solo in maniera mediata dalle emozioni e dai sentimenti, sarebbe in grado di attivare comportamenti) . Oggetti sorti incompleti dalla Grande Evoluzione e gettati in un mondo di significati artificiali e innaturali: questa è la situazione a cui conduce la nostra argomentazione difforme e provocatoria
Oggi (ieri dopo il sapiens sottosp. sapiens) il processo di cogliere l’invariante poetico è solo un tentativo nella direzione dell’esperienza di fusione originale, prima degli strani mondi, dispersivi di energia, costruiti dalla corteccia. L’invariante poetico, se vogliamo portare l’argomentazione fino in fondo, potrebbe essere colto da un solo soggetto o da un piccolo gruppo, solo se esso, in profonde intuizioni meditative, fosse capace di liberarsi dalle sovrastrutture acquisite nell’ultimo o negli ultimi salti evolutivi (per es, i Santi, i mistici di qualsiasi religione e forse anche i maghi che abbiano superato i tests del CICAP e, forse, absit iniuria verbis, anche il Nazzareno era uno di quelli!).
Concludendo, l’invariante poetico sarebbe una specie di traduzione in chiave umana e naturale dell’oggetto ‘reale’, che diventa più accessibile di altre traduzioni allo sguardo della mente umana, in quanto riproposto dal profondo interno dell’uomo, dove si riflette l’Universo.
Ad un insegnamento fondato sulla ragione, che ormai purtroppo continuerà ad essere necessario per la sopravvivenza in un mondo non naturale costruito con il primo metodo descritto e che ormai non può essere distrutto o modificato (oltre 80% del terzo mondo popperiano controlla e riflette l’ambiente artificiale in cui siamo immersi ed il terzo mondo ha vita autonoma, con forte istinto di sopravvivenza!), dovremmo affiancare con estrema cura un insegnamento dove si dia spazio alla meditazione e riflessione intuitiva, utilizzando almeno la religione o la magia e l’opera d’arte: stiamo molto attenti in particolare ai nuovi metodi razionali e strutturali che vengono sempre più proposti per la ‘lettura’ dell’opera d’arte, quasi fosse un oggetto esauribile, al posto di un maggior coinvolgimento archetipico ed emotivo, profondo.
Piero Pistoia
CURRICULUM DI PIERO PISTOIA:
piero-pistoia-curriculumok (#)
Per prendere visione di un breve curriculum dell’autore andare al termine dell’articolo
realta-da-vicino-e-da-lontano in pdf; da aggiornare…non corrisponde ancora allo scritto successivo
PREMESSA
CENNI SU LEGGI SCIENTIFICHE, ALGORITMI, PROGRAMMI E ‘CELLULAR AUTOMATA’
Esempio di automa cellulare
Figura ripresa a pag. 371 del testo di riferimento “A new kind of Science”, Publischer: Wolfram media inc. di Stephen Wolfram
DA CONTINUARE…
UNA RAPIDA RIFLESSIONE SULL’UNIVERSO: CHE COS’ E’ IL “REALE” PER I FISICI TEORICI
Da una parte, c’è, appunto, Stephen Wolfram, che a soli vent’anni al California Institute of Tecnology ottenne il PHD (dottorato) in Fisica Teorica, senza dare esami! presentando solo alcuni suoi lavori già pubblicati, con i suoi algoritmi trasferibili dal suo potente programma MATHEMATICA al Cosmo, che propone una nuova rivoluzione di idee attiva all’esterno della bottiglia col collo rovesciato di Wittgenstein. Sembra che la Natura non funzioni secondo matematica, geometria e fisica come affermava Galileo e tutti i fisici successivi; l’Universo non può ridursi ad astrazioni concettuali controllate dalla matematica, ma cresce (ontogenesi), evolve (filogenesi) come un programma su un computer, che produce una successione di eventi. Wolfram scrive nel 2002 il grosso libro della sua vita (mille pagine con altrettanti outputs di computer grafica con relativi programmi scritti a partire dalla vers. quarta del MATHEMATICA), dal titolo “A new kind of Science”, Publischer: Wolfram media inc., dove si precisa come il Cosmo nel suo complesso, compresa la vita, non è spiegabile secondo la scienza tradizionale, ma è un programma su algoritmi molto semplici che descrive e mette in atto un procedimento (es. il suo cellular automata, automa cellulare) che ‘costruisce’ foglie, alberi, nubi, le coste di isole, le forme degli animali e delle galassie… e quant’altro e non partendo da algoritmi basati su equazioni. E’ possibile individuare alcune regole semplici alla base di questo programma, ma il loro sviluppo matematico fisico di queste regole non permette di prevedere a lungo, ciò che poi è l’idea alla base della fisica della complessità (vedere i posts di questo blog relativi ai FRATTALI). In sintesi mi sembra di aver capito che Wolfram pensi di aver individuato all’interno di questo ‘programma universale’, non ancora risolvibile dal punto di vista computazionale se considerato nella sua totalità, gruppi di algoritmi che invece lo sono (per es., il suo cellular automata), che come tali (una serie ordinata di istruzioni in sequenza al di là di qualsiasi equazione matematica) un computer potrebbe elaborarli molto più velocemente di quello che farebbe la Natura, aprendo possibilità di ‘schiarire’ orizzonti futuri in anticipo, anche lontani, prima che si realizzino. Le Accademie, chiuse nella trappola di Wittgenstein, mi sembra abbiano ignorato questo evento culturale, che avrebbe potuto diventare forse anche grande (molti fisici teorici, almeno in Italia, neppure sanno chi è Wolfram e inoltre non mi risulta che il suo libro sia stato tradotto in italiano!), proprio come accadde a Galileo con la sua Natura ‘risolvibile’ in geometria, rischiando il rogo (interpretazione tout-court). Un modo di screditare l’evento mi sembra sia stato anche quello di averlo paragonato alla ‘formula universale per tutte le scoperte’ che propose Moebius, il fisico teorico della commedia grottesca ‘I FISICI’ scritta nel 1961 e rivisitata nel 1981, il cui contenuto ruotava intorno ad un manicomio. DA PRECISARE E…..CONTINUARE
Dall’altra, c’è il mondo dei fisici teorici che cerca di guardare il ‘reale’ da due importanti punti di vista:
Per chiarire questo ambiguo e duplice modo di guardare all’Universo proposto dalla fisica teorica alla ricerca della sua primigenia struttura, troviamo, nel quadro impressionista con le sue pennellate di colore individuali, un esempio analogico, ripreso come concetto dal testo “Il Bosone di Higgs”, RBA, 2015. Da qualche metro di distanza la pittura appare con le macchie di colore che sfumano costruendo la figura riportata nel quadro. Però se ci avviciniamo, la figura sembra scomparire e più guardiamo da vicino, percepiamo sempre più le macchie colorate separate. Se poi, immaginando anche che più ci si avvicina più le macchie fluttuino modificando colore e posizione (per cui in ogni punto si potrebbe trovare un qualsiasi colore, anche se con più probabilità quello corrispondente al disegno), ci si perderebbe in un caos di colori. Concludendo, anche se è vero che in un punto può apparirci anche ora un bianco ora un nero e così via, in effetti a circa qualche metro rivedo la pittura originale. Che cosa è più vero l’insieme delle macchie di colore separate o la pittura? Che cos’è allora la Realtà? Quella che vedono e con la quale interagiscono gli animali o quella che ‘vede’ il sistema di equazioni della MQR? E le emozioni, i sentimenti … che, densi, anche loro veicolano energia?
Prima della scoperta del Bosone di Higgs le particelle elementari non avevano ancora una massa?
Leggere e confrontare anche il post provocatorio dello stesso autore “La teoria e la realtà”.
CHI E’ L’AUTORE (traccia): Curriculum di Piero Pistoia
piero-pistoia-curriculumok (#)
POST IN VIA DI COSTRUZIONE: le versioni intermedie possono contenere bugs e imprecisioni!
Leggere su questo blog anche il post sulle geometrie non euclidee (GEOMETRIA E NATURA) di cui questo intervento potrebbe porsi come premessa
LA NASCITA DIFFICILE E TORMENTATA DELLE GEOMETRIE NON EUCLIDEE
Una breve scaletta di appunti per una ricerca scolastica
A cura del dott. Piero Pistoia
Al termine dell’articolo si può prendere visione di un breve curriculum di P. Pistoia
Per rileggere di più su definizioni e dimostrazioni, sfogliare un qualsiasi testo per la Scuola Media (es., Fortini-Cateni, per la Scuola Superiore).
Per le argomentazioni sul V° postulato seguiremo le linee suggerite dal testo di Mario G. Galli dell’università di Firenze “Spazio e tempo nella scienza moderna Parte I”, Ed. Cremonese
I disegnetti per le dimostrazioni sono stati ripresi dai precedenti testi e di questo ringraziamo gli autori
Due furono le convinzioni ereditate dalla Storia nel corso numerosi secoli, che ostacolarono e ritardarono la nascita delle Geometrie non Euclidee.
1 – Le convinzioni ereditate dal mondo greco, radicate nel corso di svariati secoli, che assumevano le affermazioni della geometria come ‘vere’ (raccontavano il mondo), opinione garantita dall’intuizione.
2 – La sistemazione di queste concezioni intuitive della geometria, con la formulazione dei Giudizi Sintetici a priori*, nel sistema filosofico kantiano, con la pubblicazione della sua ‘Critica della ragione pura’. Cioè tutte le affermazioni della geometria venivano sostenute definitivamente da facoltà mentali a priori e la verità della connessione mente-mondo esterno non aveva bisogno di conferme sperimentali e quindi era indipendente dall’esperienza e dall’esperimento sul mondo, pur fornendo informazioni ‘vere’ su esso (sintetiche). Forse la mente organizzava i dati sul mondo (le sensazioni) nel modo in cui riusciva a farlo, perché era costruita in quel modo acquisito nel processo co-evolutivo col mondo stesso anche se in ambiti spazio temporali limitati. Egli così giudicava la geometria come scienza assoluta della struttura dello spazio fisico.
Al tempo di Kant quindi l’interesse dei geometri non era quello di pensare a geometrie alternative per il mondo, intrappolati come erano in una bottiglia di Wittgenstein con il collo ripiegato con asola molto stretta (leggere l’art. relativo alla TRAPPOLA PER MOSCHE in questo blog)!
Nella geometria di Euclide, quella di cui si parla, esiste un postulato che già allora destava sospetto, il V° postulato del suo sistema geometrico che può essere così espresso: da un punto non appartenente ad una retta si può condurre una ed una sola parallela alla retta data. Per questo postulato, parlando della parallela condotta da un punto ad una retta data, si dovrà dire la parallela e non una parallela.
_______________________________
UN INTERMEZZO DI BREVE RETROSPETTIVA – Già era stato dimostrato il teorema che per un punto esterno ad una retta era possibile tracciare una ed una sola perpendicolare alla retta data (che poteva utilizzare il precedente teorema sulla esistenza ed unicità della bisettrice) e, come conseguenza, il teorema che, per un punto esterno ad una retta si può condurre una seconda retta non avente alcun punto in comune con la prima, ottenendo così due rette sullo stesso piano non aventi punti in comune dette rette parallele (definizione). Da questa definizione, ne deriva una nuova formulazione del teorema precedente, che per un punto dato è possibile condurre una parallela ad una retta data. Di conseguenza, come era accaduto per la perpendicolare, se esiste una retta parallela ad una data, nasce la domanda se questa sarà unica. Se non riusciamo a ‘costruire’ quest’ultimo teorema (unicità della parallela) dal lato puramente razionale è arbitrario l’ammettere o no tale unicità (per un punto fuori da un retta sarebbe cioè possibile tracciare una, più di una o nessuna retta parallela alla retta data!). Nella geometria euclidea, non potendo dimostrare questo, fu introdotto sotto forma di postulato, appunto il V°!
________________________________
Infatti già Euclide, chiaramente indipendentemente dai kantiani, sembrò essere molto perplesso sul suo V° postulato**, se aspettò a dimostrare almeno trenta teoremi indipendentemente da esso, prima di introdurlo.
D’altra parte anche ai geometri al tempo di Kant sembrò avessero dei dubbi; infatti ritenevano il V° sì necessario ed evidente, ma molto più complesso degli altri. Infatti i geometri in generale, pur ammettendo che tutti i postulati proposti erano di per sé evidenti, non lo erano tutti nello stesso modo. Si posero il problema se il V° potesse essere indipendente dagli altri. Bastava controllare come ipotesi, se usando gli altri (postulati o teoremi da essi dedotti), si potesse impostare un teorema che avesse come tesi il V° postulato.
Se fossero riusciti ad articolare questa dimostrazione, che cosa avrebbero ottenuto? Non avendo altre perplessità su altri postulati, forse il tempo per proporre geometrie alternative si sarebbe molto allungato, o forse la nuova geometria ottenuta avrebbe ‘matchato’ (part. pass. italianizzato da matching ***, alternativo di fitting), il mondo (geometria assoluta)!!! Lo stesso Bolyai nel 1832 chiamò assoluta la geometria dedotta usando tutti i postulati di Euclide eccetto il V° (una trentina di teoremi). Ma oggi sembra che il valore attribuito in generale a tutti i postulati non sia diverso da quello attribuibile al V°.
Quando è possibile allora sostituire il V° postulato con uno completamente diverso?
risp.1: quando il V° postulato risultasse non derivabile dagli altri, cioè fosse dagli altri indipendente!
risp.2: qualora la geometria non fosse una scienza
Al tempo ci furono tentativi svariati di dimostrare questo tormentato teorema indipendentemente da varie parti e su vari fronti. Teoremi tutti coerenti e tutti sembravano ‘colpissero’ in maniera precisa la tesi, ma…****
Tutte queste argomentazioni critiche stavano contribuendo a costruire un aspetto del Terzo Mondo di Popper e già si abbozzavano alla sua frontiera gli incastri che soddisfatti avrebbero precisato le idee delle nuove geometrie: il tempo della loro origine si avvicinava.
DI QUESTI TENTATIVI NE FAREMO ESEMPI NEL PROSIEGUO
Cliccando sopra otteniamo lo scritto successivo rivisitato (vers. 10) in pdf, in ordine migliore e in parte corretto, anche se non definitivo.
_______________________________________________________________________
DA CONTINUARE……
ALCUNI TEOREMI DI RETROSPETTIVA DI GEOMETRIA EUCLIDEA PIANA
Disegnetti da Fortini-Cateni
Definizione di bisettrice di un angolo: la bisettrice è la semiretta che divide l’angolo al vertice in due angoli uguali
Si dimostra che, per qualsiasi angolo (convesso, concavo, piatto), la bisettrice esiste ed è una sola.
Accenniamo al caso dell’angolo convesso. Sui lati prendiamo dal vertice A due segmenti uguali (AD=AE) e congiungiamoli. Prendiamo un punto F all’interno dell’angolo e congiungiamolo a D e a E. Se l’angolo FDE è diverso da FED, per es., minore, da E tracciamo la semiretta EH che forma un angolo DEH=EDF e incontra DF nel punto G (postulato). Il triangolo il triangolo DEG è isoscele. Si considerino i due triangoli ADG e AEG che sono uguali per il III° criterio di uguaglianza dei triangoli. Ne deriva che la retta AG è la bisettrice. Essa è unica perché ogni altra divide l’angolo al vertice in pari disuguali.
Consideriamo ora la bisettrice dall’angolo piatto. si prenda un punto D all’interno dell’angolo e lo si unisca con A; se l’angolo BAD e CAD risultano uguali, la semiretta AD è la richiesta; se invece sono disuguali, sulla maggiore costruiamo la semiretta AE in modo che l’angolo BAE sia uguale all’angolo CAD; otteniamo un angolo EAD che è convesso; cioè esiste una semiretta AF che lo divide in parti uguali.
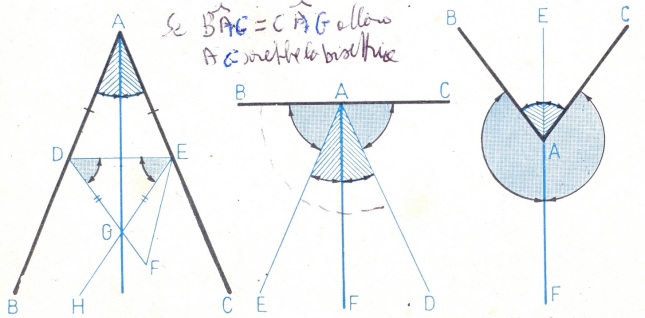
Semiretta che biseca un convesso un angolo piatto un angolo concavo
Unicità della bisettrice nel caso dell’angolo convesso BAC. Ogni altra semiretta AH diversa da AG, lo divide in parti disuguali. Infatti dalla figura abbiamo BAH>BAG=GAC>HAC a maggior ragione BAH>HAC. IL ragionamento è analogo per gli altri due angoli c.v.d.
Se l’angolo BAC è concavo, sia AE la semiretta che dimezza l’angolo convesso che ha gli stessi lati. Si tracci la semiretta AF opposta ad AE che divide l’angolo concavo BAC in due parti uguali. Infatti gli angoli FAB E FAC risultano uguali perché supplementari (la loro somma è un angolo piatto) dei due angoli uguali BAE e CAE.
_________________________________________
Definizione di perpendicolare: la perpendicolare da un punto esterno P ad una retta è la semiretta da P che fa due angoli uguali sulla retta, cioè due retti; la perpendicolare tracciata da un punto O qualsiasi della retta, è la semiretta che parte da O e costruisce due angoli retti sulla retta.
Come conseguenza, nel caso di una perpendicolare da un punto C (vedere sotto) fuori di una retta condotto alla retta è esistente ed unica. Facendo ruotare il semipiano di C intorno alla retta e tornando indietro, ottengo l’immagine del punto C, cioè D nell’altro semipiano. Si colleghi C e D ottenendo il punto di intersezione sulla retta, O. Vogliamo dimostrare che la retta CD forma con la retta AB angoli uguali. Ripetendo la rotazione la semiretta OC si sovrappone alla OD e l’angolo BOC si sovrappone all’angolo BOD e quindi sono uguali e la retta CD e perpendicolare a AB.
La perpendicolare è unica perché, tracciando CF, si forma il triangolo COE di cui l’angolo CEB è esterno maggiore di ogni angolo interno non adiacente (anche del retto).
Dimostriamo ora l’esistenza e l’unicità del punto medio di un segmento.
Dalle due figure sopra, dimostrato dalla prima che in un triangolo isoscele la bisettrice dell’angolo al vertice è perpendicolare alla base e la divide per metà, consideriamo nella seconda il segmento AB e un punto C, e colleghiamolo con A e B. Se l’angolo CAB è diverso dall’angolo ABC per es., minore, sul maggiore tracciamo una semiretta BD che faccia un angolo uguale a CAB e incontri AC nel punto E. Colleghiamo E con F. All’interno di un angolo, qualsiasi retta dal vertice attraversa sempre i segmenti che collegano qualsiasi coppia di punti presa sui lati (postulato). Si ha così un triangolo isoscele con gli angoli alla base uguali (lati obliqui uguali). Tracciamo la bisettrice dell’angolo al vertice AEB che per il teorema precedente è anche altezza e divide la base in due segmenti uguali. Il punto F è il punto medio del segmento AB. Esso è unico perché per un qualsiasi altro punto G,
AG>AF=FB>FG, a maggior ragione
AG>GB
_________________________________________________
I disegnetti successivi sono ripresi da M. Galli
Teoremi dell’angolo esterno di un triangolo
Dato il triangolo ABC si prolunghi il segmento AB e tracciamo una semiretta da A passante per il punto medio M, che è esistente ed unico (vedere il teorema già dimostrto), del segmento BC. La semiretta da A a D, interna all’angolo CAB incontrerà certamente (postulato) il segmento CD che collega una coppia di punti sui due rami dell’angolo. Su tale semiretta prendiamo un punto D tale che AM=MD. I due triangoli AMC e BMD sono uguali per il primo criterio di uguaglianza dei triangoli perché hanno uguali gli angoli AMC e BMD perché opposti al vertice e il lati CM e AM del primo triangolo sono uguali rispettivamente a a MB e MD del secondo per costruzione. Ma in triangoli uguali a lati uguali si oppongono angoli uguali, per cui sono uguali gli angoli ACM E MBD (gamma). D’altra parte la somma degli angoli beta (β) e gamma (γ) sono minori di due retti, in quanto γ è interno all’angolo esterno, c.v.d.; d’altra parte dalla figura l’angolo esterno (di lati BC e prolungamento di AB) è maggiore di γ che ne è una parte, per cui è maggiore dell’angolo interno non adiacente, c.v.d. La dimostrazione può essere ripetuta su ogni lato. Manca la relazione fra l’angolo esterno e la somma degli interni non adiacenti.
Con il teorema appena dimostrato che la somma di due angoli interni di un triangolo è minore di due retti, dimostriamo la prima parte del postulato V°, cioè l’esistenza di una parallela alla retta data per un suo punto esterno.
TEOREMI SULLA PARALLELA
Da P conduciamo la perpendicolare alla retta r; sia questa PQ. Conduciamo per P la retta s perpendicolare a PQ. Ne consegue che gli angoli alfa (α) e beta (β) sono uguali e retti. Se la retta r incontrasse la retta s, le due rette con PQ formerebbero un triangolo con la somma degli angoli superiore a 2 retti. Questo è assurdo per il teorema precedente. Si conclude che le due rette sono parallele, per cui esiste una retta parallela (la s) alla retta r passante per P.
Ma questa parallela è unica? Ora se consideriamo un’altra retta k passante per P e distinta da r, siamo sicuri che questa incontri ad un certo punto r? Euclide ipotizza che si incontrino dalla parte del piano dove la somma degli angoli corrispondenti è minore di 2 retti. Questo è il cuore del quinto postulato intuitivo, ma forse più complesso degli altri. Il fatto che due rette prolungate non si incontrano mai (rette parallele), significa che sono anche equidistanti? Nel tempo fu proposto di definire una parallela ad un’altra come la retta da essa equidistante. La proposizione ‘il luogo dei punti equidistanti da una retta data appartengono ad un’altra retta parallela alla prima’, è sostenuto dalla nostra intuizione, ma non è derivabile dagli altri postulati, come l’unicità della retta parallela per un punto esterno; in questa proposizione è contenuto già il V° postulato. Quindi si tratta di un postulato analogo al V°. Se sostituissimo al quinto la detta definizione potremmo dimostrare con altri postulati e teoremi che la retta passante per P e non intersecante l’altra, è unica, cioè il quinto postulato!
Gli antichi matematici, come già accennato, tentarono di dimostrare questo strano postulato (croce e scandalo della geometria elementare, come ebbe a dire D’Alambert), ma i loro tentativi non sortirono altro effetto che quello di sostituire al postulato di Euclide altri postulati del tutto equivalenti. Le affermazioni di partenza di questi matematici nascondevano un postulato analogo a quella da dimostrare!
Così, volendo eliminare il V° postulato, iniziando l’argomentazione con il teorema degli angoli interni del triangolo dimostrato anche con il V° di Euclide, potremmo raggiungere deduttivamente anche l’unicità della retta parallela. Dovremmo però sostituire tale teorema come postulato del sistema al posto del V°. L’obbiettivo di dimostrare il V° eliminandolo falliva, anche perché il nuovo postulato era meno intuibile del vecchio. Si potrebbe a questo punto continuare a tentare di dimostrare il teorema degli angoli interni di un triangolo escludendo il V°, indirettamente trasformando il V° in teorema, ma tutti i tentativi fallirono.
PREMESSA L’EQUIDISTANZA DI DUE RETTE, L’ UNICITA’ DELLA PARALLELA SEGUE LOGICAMENTE
Il postulato dell’unicità della retta per il quale non è possibile proporre una logica spiegazione, in effetti contiene le seguenti proposizione
1 – L’intuizione suggerisce che posano esistere due rette equidistanti, cioè che il luogo dei punti equidistanti da una retta debba essere un’altra retta.
2 – Se due rette si incontrano in un punto O, è intuibile che presi due punti equidistanti da O, OP = OQ, se la distanza OP cresce oltre ogni limite anche il segmento PQ cresce oltre ogni limite.
Ammesso questo come postulato dell’equidistanza, è possibile dimostrare che una retta non equidistante debba incontrare l’altra, cioè l’unicità della retta che diventa un teorema!
Si dimostra col V° postulato che OP e PQ sono direttamente proporzionali. Senza il V°, Euclide dimostrò che se OP supera ogni limite lo fa anche PQ e dimostrò che una spezzata condotta fra due punti è più lunga del segmento di retta che li unisce eche in un triangolo rettangolo l’ipotenusa è più lunga di ogni cateto. Cos in un triangolo rettangolo ‘coperto’ da una successione di angoli come quello sopra, di ha: OA < n*AB e AB > OA/n se il segmento OA tende all’infinito lo fa anche AB.
Dalla figura, tenendo conto delle argomentazioni precedenti risulta che spostando M oltre ogni limite anche il segmento MK fa altrettanto; infatti raddoppiando la figura coll’angolo OKN, spostando M verso l’infinito, analogamente si comporta il segmento MN come già dimostrato; per cui anche il segmento MK, cioè la distanza dalla retta OB, la metà di MN, fa altrettanto.
Ne consegue il seguente teorema conclusivo:
Siano r ed s due rette equidistanti (fig. sopra) e sia delta la loro distanza. Si consideri un’altra retta k che formi con r un angolo alfa piccolo a piacere. Procedendo lungo questa retta la distanza PM deve crescere oltre ogni limite, uscendo uscendo ad un certo punto dalla striscia compresa fra le due rette, incontrando la retta s, di qui l’unicità della parallela.
PREMESSA LA SOMMA DEGLI ANGOLI DI UN TRIANGOLO UGUALE A DUE RETTI, SI PUO’ DIMOSTRARE L’UNICITA’ DELLA PARALLELA
Qui va il disegno di una retta orizzontale con due perpendicolari verticali in A e B
Si abbia una retta orizzontale v che passa per i punti A e B; da essi tracciamo verso l’alto due rette r ed r’ perpendicolari a v. Si deve dimostrare che r ed r’ siano equidistanti (AB=PQ), in quanto abbiamo dimostrato prima, che equidistanza implica unicità.
I due triangoli APQ e ABQ sono uguali perché hanno due lati uguali e l’angolo compreso (alfa=alfa1), per il primo criterio di uguaglianza. Alfa è uguale da alfa1 in quanto alfa1+beta1 =90° e anche alfa+beta1=90° per cui alfa ed alfa1 sono complementari dello stesso angolo beta1. Alfa1+beta1 sono un retto perché k1= un retto e la somma di alfa1+beta1+k1 (somma angoli di un triangolo, ipotesi iniziale) = 2 retti. Ne deriva l’uguaglianza di AB=PQ e, poiché la coppia PQ è arbitraria, le due rette r e r1 sono equidistanti e per il teorema già dimostrato ne consegue l’unicità della parallela. c.v.d.
Possiamo ottenere lo stesso risultato in un modo diverso. E’ necessario introdurre prima un lemma.
Definizione di Lemma: proposizione importante per la dimostrazione di un teorema successivo.
Ammesso come postulato il teorema della somma degli angoli interni di un triangolo, è possibile come primo passo costruire un triangolo rettangolo con uno degli angoli acuti minore di una quantità piccola piacere (lemma)
Dalla figura sotto siamo partiti da costruire un triangolo retto e isoscele BAC, sia omega uno degli angoli acuti uguali. Prolunghiamo AC e sulla prolunga segnamo un punto C1 tale CC1 sia uguale a BC. Si ha il triangolo isoscele in cui CC1B=CBC1 . I due angoli sono gli interni non adiacenti dell’angolo esterno ACB. Sapendo che l’angolo esterno di un triangolo è uguale alla somma dei due interni non adiacenti si ha che l’angolo esterno al triangolo BCC1 è uguale alla somma degli angoli CC1B+CBC1; se chiamiamo il valore comune dei due angoli non adiacenti ω1, ω=2*ω1 e ω1=ω/2. Possiamo continuare la costruzione prendendo sul prolungamento di AC il punto c2 tale C1C2=BC1; ne risulta un nuovo triangolo isoscele BC1C2 con angolo esterno ω/2 e angoli interni non adiacenti ω/4 e cosi via. Se facciamo n costruzioni come le precedenti si giunge ad un triangolo rettangolo dove l’angolo sul prolungamento sarà ω/2^n. Se n diventa sempre più grande avremo un triangolo rettangolo con uno degli angoli acuti piccolo a piacere. c.v.d.
Con il risultato del teorema precedente sarà facile dimostrare l’unicità della parallela.
Dimostriamo il teorema che, se la somma degli angoli interni di un triangolo è due retti (postulato di partenza), allora è ‘vera’ l’unicità della parallela, che cessa di essere a sua volta un postulato.
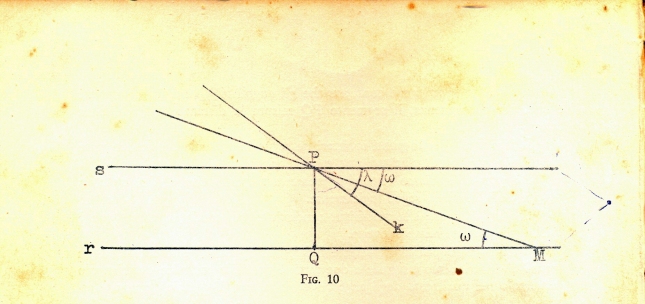
Consideriamo un punto P fuori della retta r. tracciamo da P la perpendicolare ad r incontrata in Q; conduciamo poi per P la retta s perpendicolare a PQ. Ipotizziamo che la retta s non possa incontrare la retta r. Conduciamo ora attraverso P un’altra retta non coincidente con s ed ammettiamo che formi con PQ un angolo inferiore ad un retto, il cui complementare (che è l’angolo che sommato al precedente dà un retto) lo chiameremo lambda (λ). Costruiamo il triangolo QMP di cateti PQ e QM. Come abbiamo visto nel precedente lemma, QM potrebbe essere così lungo che l’angolo QMP possa divenire più piccolo di una quantità qualsiasi assegnata, anche minore di λ. Ammesso che la somma degli angoli di un triangolo sia due retti, l’angolo che la retta PM forma con s deve divenire minore di λ. Allora la retta K, interna all’angolo QPM, incontrando PM la r, a maggior ragione incontrerà anch’essa r. Così ammettendo come postulato il teorema della somma degli angoli di un triangolo, ammettiamo anche il postulato di Euclide (V°) con tutte le conseguenze. Così la geometria elementare, anche quella studiata nella scuola media, rimarrebbe immutata nella sostanza. Ma il teorema degli angoli del triangolo è certamente meno intuitivo del V° postulato, anche se forse più controllabile con con un esperimento, considerando l’affermazione come un goal regolativo; difficile sarebbe invece controllare sperimentalmente cosa fa una ‘parallela’ molto lontano!) DA CONTROLLARE….
PROPRIETA’ RELATIVE ALLA SOMMA DEGLI ANGOLI DI UN TRIANGOLO; USANDO I POSTULATI EUCLIDEI SENZA IL V°
La dimostrazione è dovuta a Legendre, riportata da Galli, che “In nessun triangolo la somma dei suoi angoli interni non può mai superare due retti”. Come conseguenza si apriranno così le due possibilità che ; 1) sia uguale a due retti; 2) sia minore di due retti.
Consideriamo la figura sotto analoga a quella precedente per dimostrare i teoremi dell’angolo esterno di un triangolo. Sia ABC il triangolo primitivo; si prolunghi il lato BC in CD; sia M il punto medio del segmento BC (che esiste ed è uno solo); si unisca A con M e sul suo prolungamento si prenda il segmento MC’=AM; si tracci la semiretta di origine B e passante per C’;essa cade necessariamente all’interno dell’angolo CBD dove BD è il prolungamento di AB. Confrontando il triangolo primitivo ABC con ABC’, tenendo conto che gamma=gamma’, che epsilon =epsilon’, si vede chiaramente che la somma degli angoli del triangolo ABC è data da epsilon + lambda + beta + gamma; la somma nel triangolo ABC’ è: beta + gamma’ + epsilon’ + lambda; ne deriva che le due somme sono rigorosamente uguali.
Inoltre il triangolo ABC’ ha un angolo che è minore od uguale alla metà di uno degli angoli del triangolo di partenza ABC. Infatti la retta AC’ divide l’angolo alfa del triangolo ABC in due parti epsilon e lambda in generale diverse; una cioè lambda, è comune ai due triangoli e l’altra, epsilon è uguale ad un angolo, epsilon’ del nuovo triangolo ABC’. Nel nuovo triangolo allora ci sono due angoli, epsilon’ e lambda che sommati danno alfa, angolo del triangolo primitivo. Se sono uguali, caso poco frequente, si può affermare che il nuovo triangolo ABC’ possiede un angolo che è la metà di alfa e, se sono diversi, caso più frequente, il nuovo triangolo possiede un angolo minore della metà di alfa. Concludendo, vedere lo scritto ‘arruffato’ sulla figura
“qualunque cosa accada, potremo concludere che il nuovo triangolo possiede un angolo che è minore o al più uguale alla metà di alfa” M. Galli opera citata.
Ma la costruzione fatta su ABC possiamo ripeterla su ABC’ ottenendo un terzo triangolo su cui applicare lo stesso ragionamento e così via. Supponendo di fare n costruzioni analoghe potremmo ottenere alla fine un triangolo che ha la stessa somma degli angoli come l’originale ABC e un angolo molto piccolo, minore od uguale a alfa/2^n, dove alfa è l’angolo del triangolo ABC di partenza.
CONCLUSIONI DEL TEOREMA DI ADRIEN LEGENDRE (1752-1833) CHE DEFINISCE GLI INCASTRI POTENZIALMENTE NECESSARI ALLA NASCITA DELLE GEOMETRIE NON EUCLIDEE, SITUATI SULLA ‘SUPERFICIE’ DEL TERZO MONDO DELLE ‘IDEE’ DI POPPER
Tenendo conto del teorema precedente, ammettiamo, per assurdo, che la somma degli angoli del triangolo ABC sia maggiore di due retti anche di una quantità molto piccola delta.
SOMMA ANGOLI DI ABC = 2 retti + delta
Nella costruzione precedente a triangoli successivi la somma dei loro angoli non può cambiare per postulato iniziale e così anche il valore della somma nel triangolo finale, di cui un angolo diventerà così piccolo da non superare alfa/2^n e gli altri due angoli insieme saranno minori di due retti, come dimostrato precedentemente, senza usare il V° postulato. Se n è così grande da rendere alfa/2^n minore di delta avremo che :
SOMMA ANGOLI DI ABC < 2 retti + alfa/2
asserzione che contraddice la formula precedente. Ne consegue che la somma degli angoli di un triangolo non può mai superare 2 retti! Si apre ora così la possibilità per le due affermazioni accennate all’inizio.
1 – La somma degli angoli di un triangolo è uguale a due retti.
2 – La somma degli angoli di un triangolo è minore di due retti.
Ma nascosto nelle pieghe del nostro teorema esiste un postulato euclideo fin’ora taciuto! Il susseguirsi delle nostre costruzioni sarebbe stato impedito dalla lunghezza della retta, in quanto se AM, che aumenta con n, non potesse essere raddoppiato sul suo prolungamento il processo si interromperebbe. Il postulato euclideo da focalizzare afferma che la retta è infinita! Una ‘retta’ disegnata su una sfera invece ha lunghezza finita, anche se illimitata, aprendo la possibilità per i triangoli sferici di avere la somma degli angoli interni maggiore di 2 retti.
GEOMETRIA E SCIENZA FISICA
Dal punto di vista della scienza fisica, l’interesse non va alla geometria non-euclidea come tale ma al notevole effetto che ebbe sul concetto di spazio nella fisica moderna. Non solo essa condusse ad una migliore comprensione della natura ipotetica della geometria assiomatica pura, ma alla chiarificazione del concetto di spazio fisico rispetto allo spazio matematico. Con la scoperta della geometria non euclidea fu chiaro che non esistevano mezzi a priori, cioè dal punto di vista logico matematico, quale tipo di geometria avrebbe descritto le relazioni spaziali fra i corpi fisici. Era naturale quindi interpellare l’esperimento per stabilire se il problema della vera geometria poteva essere deciso a posteriori. Per la misura degli angoli bisognava rivolgersi ai movimenti astronomici per ovviare ad errori di misura. Riemann parlò di spazio generalizzato di cui la geometria euclidea, quella ellittica di Lobacevsky e Bolyai e la sua sferica erano casi particolari, dando impulso allo sviluppo della moderna analisi tensoriale, che confinata fino ad allora ai problemi di elasticità, divenne un mezzo essenziale sia per la matematica superiore sia per la fisica teorica.
_____________________________________
Siamo giunti così nella zona storica di transizione alle Geometrie non euclidee, l’iperbolica di A. Bolyai (1802-1860), Nicolai Ivanovic Lobacevsky (1793-1856), e la geometria sferica di B. Riemann (1826-1866) e con questo terminiamo, e per entrare nel vivo di questo nuovo ambiente culturale vedere anche il post riportato in questo blog dal titolo ‘Geometria e Natura’, a più voci.
Dott. Piero Pistoia
CHI E’ L’AUTORE (traccia): CURRICULUM DI PIERO PISTOIA
Curriculum di piero pistoia:
piero-pistoia-curriculumok (#)
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
LA TEORIA, LA REALTA’ E I LIMITI DELLA CONOSCENZA
Considerazioni provocatorie
a cura del Dott. Piero Pistoia (vers. rivisitata)
Le Teorie scientifiche sono nostre invenzioni e, talora, procedendo, come afferma Galileo (1), “contro le sensate esperienze” e “facendo violenza al senso”, sono così audaci da ‘scontrarsi’ con la Realtà; e’ appunto da questo “scontro” veniamo a conoscere che il Reale esiste (2). Questa posizione (3) considera errata la concezione secondo cui le teorie scientifiche debbono essere fondate su ciò che di fatto osserviamo, cioè sui dati forniti dal Reale, o perché riconducibili a puro compendio e organizzazione di essi (Circolo di Vienna) o perché conformate da proposizioni molecolari teoriche, scomponibili in atomi linguistici immediatamente rapportati ai dati immediati dell’esperienza (Wittgenstein).
La Teoria non è riducibile ad asserzioni protocollari (dice molto di più di quanto possiamo sottoporre a controllo), per cui l’empirico non è più sorgente di significati per essa, serve solo, attraverso la logica del modus tollens (vedere dopo), a ricercarne, continuamente e senza fine, la falsificazione.
La Teoria così non è costruita a partire dai dati secondo processi di generalizzazione riassunti dal concetto di Induzione, che, sfuggendo a qualsiasi dimostrazione logica, ha la propria origine nella neuro-fisiologia animale e serve solo alla costruzione di una classe di convincimenti psicologici (certezze, ma non verità).
Essa non potrà mai essere “verificata” dai fatti, perché il procedimento (fallacia dell’affermare il conseguente): “se H implica S e S è vero, allora H è vera”, non è un procedimento logico fino in fondo.
La Teoria potrà invece essere falsificata dai fatti tramite il procedimento deduttivamente valido (modus tollens): “H implica S e S è falso, allora H è falsa” (4).
Se poi nell’analizzare la zona di “scontro” (falsificazione) rinveniamo ancora processi a logica debole come l’Induzione, ovvero, data la complessità teorica degli oggetti in gioco (5), rimane oscuro e indeterminato ciò che viene falsificato, allora le teorie rimarranno semplici invenzioni della mente, convenzioni sostenute ora da paradigmi a forte permeabilità sociale (Kuhn), ora dai successi dei Programmi di Ricerca (Lakatos).
Ma allora il sostegno delle Teorie scientifiche non è più qualcosa di solido e oggettivo: prende il sopravvento l’aspetto convenzionale, arbitrario, propagandistico e strumentale, nel senso che esse diventano solo efficienti strumenti per la modifica più radicale dell’ambiente (teorico e fisico) a favore di una sopravvivenza (culturale e fisica) ad oltranza degli umani. Le teorie diventano convenzioni arbitrarie semplici ed efficaci, funzionali ai fatti, anche se non funzione dei fatti.
Si indebolisce così, in termini di principio, la distinzione da altre attività della mente umana con gli stessi obbiettivi (6) come le teorie del senso comune e del buon senso, il mito e la magia, la fede e il misticismo…(Epistemologia Anarchica).
La teoria scientifica diventa un’invenzione che non costruisce mappe del Reale, ma vi inventa sentieri e vi disegna “di brutto” depressioni e rilievi, aprendosi la strada man mano che procede. Il poeta Antonio Machado (7), in grande poesia, esprime questa azione conoscitiva umana:
Viandante, son le tue orme la via ,
e nulla più;
viandante non c’è via,
la via si fa coll’andare.
Con l’andare si fa la via
e nel voltare indietro la vista
si vede il sentiero che mai
si tornerà a calcare.
Viandante, non c’à via
ma scie sul mare.
Già Kant aveva affermato che “l’intelletto non attinge le sue leggi dalla Natura ma le prescrive (quaestio iuris) ad essa” (8) e altrove (9) che “l’Intelletto vede solo ciò che esso stesso produce secondo il suo disegno”.
Ciò che ne emerge è una topografia nuova di zecca, inventata e costruita dall’Uomo per L’Uomo ed è questo il suo Universo, “vero”, perché funziona, è adatto ed adeguato (l’inglese fitting, o il passen tedesco).
Verum ipsum factum, aveva detto Vico molto tempo prima: ciò che l’Uomo “crea” con le sue mani è “vero” per l’uomo, cioè funziona nell’ambiente in cui l’uomo opera, permettendo di modificare tale ambiente fenomenico esterno e interno ai propri fini.
Allora non è dell’Uomo la conoscenza assoluta del Reale, visto come una congerie di infinite possibilità razionali e irrazionali di stati di un “qualcosa”, dove neppure il prima e il dopo, il sinistro e il destro, il sopra e il sotto corrisponderanno all’esperienza umana (Noumeno kantiano).
Nessuna concordanza o corrispondenza di immagine (match e in tedesco stimmen) quindi fra conoscenza e realtà, a differenza delle concezioni tradizionali e della Psicologia Cognitiva, sostiene con forza il Costruttivismo radicale (10).
Forse siamo davvero chiusi in un “trappola per mosche”, costituita da una bottiglia la cui sommità è un imbuto rovesciato. Dall’interno l’unica apertura appare alla mosca come la soluzione meno probabile e la più irta di ostacoli e da essa distoglie l’attenzione. E’ meno gravoso organizzarsi all’interno della trappola che trovare la via.
Come uscire allora da questa trappola che, metaforicamente, rappresentala nostra inadeguatezza nella soluzione dei problemi conoscitivi? Data la configurazione, le soluzioni andranno cercate nei luoghi più improbabili, fuori dalle credenze comunemente accettate, al di là delle abitudini dipensiero, negando cioè tutto ciò che compone il nostro attuale sistema di riferimento: la soluzione è infatti dove c’è più rischio. Non per niente ci si accorge poi che ogni fatto che sia stato oggetto di rifiuto più astioso e viscerale e limitato dalle repressioni più crudeli, stranamente, possedeva la sconcertante capacità di porre problemi insidiosi, ma che schiudevano nuove vie.
All’interno, quindi, il quadro concettuale appare coerente e privo di contraddizioni: il sistema di credenze, “dentro”, si auto-giustifica continuamente e tutti gli atti (osservazione, giudizio, valutazione…) vengono compiuti dal punto di vista particolare del sistema stesso. Se vogliamo uscire è necessario inventare un nuovo e inusitato sistema di certezze da cui “guardare” la situazione: è allora che riusciamo a individuare improvvisamente l’apertura. Una volta usciti ci troviamo però in un’altra trappola che ingloba la prima e così via all’infinito: ciò che progredisce è solo l’adeguatezza delle teorie (fitting e non matching) che diventano sempre più funzionali ai nostri fini.
Questa configurazione indeterminata di trappole includenti sarebbe poi la conseguenza di un’ unica trappola inesorabile, cioè l’impossibilità totale della distinzione fra soggetto e oggetto. L’Io stesso è la visione dell’Universo, affermava il premio Nobel per la Fisica Schroedinger. Il confine di separazione fra Io e Universo si perde in frattali indefiniti e la sua ricerca rincorre descrizioni, di descrizioni, di descrizioni…. La poesia di Montale, trascritta di seguito (commentata nel post a più dimensioni in questo blog), sottolinea questa impossibilità di raggiungere tale limite da “dentro” (Non chiederci la parola che squadri da ogni lato/ l’animo nostro informe…) e da “fuori” (Non domandarci la formula che mondi possa aprirti…).
NON CHIEDERCI LA PAROLA
Non chiederci la parola che squadri da ogni lato
l’animo nostro informe, e a lettere di fuoco
lo dichiari e risplenda come un croco perduto
in mezzo a un polveroso prato.
Oh l’uomo che se ne va sicuro,
agli altri e a se stesso amico,
e l’ombra sua non cura che la canicola
stampa sopra uno scalcinato muro!
Non domandarci la formula
che mondi possa aprirti, sì qualche
storta sillaba e secca come un ramo,
codesto solo oggi possiamo dirti, ciò
che non siamo, ci che non vogliamo.
Quindi come nell’incisione: “Galleria di Stampe” di Escher (vedere figura), l’Io, in basso, osserva un mondo (nave e fila di case lungo costa), che si trasforma nel substrato che lo produce (casa d’angolo in alto a destra dove si apre proprio la galleria dov’è l’Io che guarda). Non esiste alcun luogo da dove uscire (confine): se tentassi di farlo (risalire all’inizio di un mio pensiero o idea) mi troverei nel bel mezzo di un frattale in continua regressione, perdendomi in una infinità di dettagli e interdipendenze (il circolo interminabile che sfuma nello spazio vuoto al centro della figura).
Ma allora il Paradosso non è semplicemente una curiosità intellettuale, ma si nasconde fra le pieghe dello stesso atto conoscitivo: correndo lungo un ramo di iperbole, non è da escludere che, in questi contesti, i due famosi professori in medicina, il Corvo e la Civetta, del libro di Pinocchio, ricordati con maestria e precisione da Collodi, avessero ragione ambedue.
Da questo insieme compenetrato e circolare di Io e Universo è mai possibile “saltar fuori”? L’”ombra”, di cui si parla nella poesia, porta scritto qualche segreto? Sarà forse più facile l’accesso al Reale tramite l’esperienza mistico-religiosa, l’esperienza artistica e quella magica?
Quest’ultime due, profondamente legate al loro sorgere (si pensi ai significati dell’arte Paleolitica nelle grotte di Lascaux), hanno lasciato di tale interazione tracce nell’arte di tutti i tempi (si pensi agli strani cieli a misura d’uomo di Van Gogh), anche se abbiamo perso la consapevolezza di questi profondi significati archetipici.
Già lo stesso B. Russel affermava che “non vi era alcuna ragione definitiva di credere che tutti gli accadimenti naturali avvengano secondo leggi scientifiche” (11). La discontinuità del tempo e dello spazio e la quantizzazione del microcosmo individuavano “zone d’ombra” a regime caotico, per cui “l’apparente regolarità del mondo sarebbe dovuta alla completa assenza di leggi”.
Non è trascurabile il fatto che scienziati e filosofi abbiano mutuato dalla Fenomenologia di Husserl (12) la parola “einfuhlung” (immedesimazione, empatia) per spiegare l’illuminazione che la mente subisce quando “inventa” ipotesi creative sul cosmo.
Il grande logico Ludwig Wittgenstein nel suo Tractatus Logico-Philosophicus (13) alla proposizione 6.52 scriveva “Noi sentiamo che se tutte le possibili domande della scienza ricevessero una risposta, i problemi della nostra vita non sarebbero neppure sfiorati” e successivamente, alla 6.522, “C’è veramente l’Inesprimibile. Si mostra, è ciò che è mistico”.
Esiste allora un immenso mare del magico e del mistico che circonda oscuro e tempestoso la piccola isola del razionale, anche se poi di questo “altro” (mare) non se ne può parlare (1° Wittgenstein), e degli altri infiniti “giochi linguistici” possibili sul mondo (isola), nessuno è plausibile, perché non c’è realtà “là fuori“ (2° Wittgenstein). E’ vero: spesso nelle esperienze mistiche e forse magiche, dove per pochi secondi soggetto e oggetto si fondono nella stessa unità primordiale, le descrizioni sono vaghe e soggettive; “il Tao che può essere espresso non il vero Tao” (14). Ma, per esempio, nel caso della situazione di Einfuhlung nella ricerca scientifica, mi sembra, che le cose siano leggermente diverse (si pensi all’ipotesi creativa che risolve un problema cruciale del mondo). Se questo fosse vero, forse sarebbe possibile non solo pronunciare qualche “storta sillaba”, ma balbettare qualche parola e sarebbe già qualcosa in termini di principio.
Il presupposto dell’esperienza magico-mistica che fa corrispondere puntualmente la struttura reale del Cosmo a quella della mente umana, permetteva l’accesso ai segreti più nascosti della Natura attraverso la meditazione e la contemplazione sull’Universo.
Si pensi a Giordano Bruno (15), che apriva un canale di comunicazione reversibile fra l’Uomo e Dio, percorribile, dal basso all’alto, tramite l’esperienza magico-mistica e la contemplazione su un Universo infinito (per questo fu bruciato vivo). Per lui la scienza e il copernicanesimo, a differenza di Galileo, che per questo salvò la vita, non erano altro che metafore e gli errori, che nell’interpretazione scientifica di esse commetteva, erano di nessun conto di fronte al potere che pensava di schiudere all’umanità ( la conquista del Vero contro l’apparente). Lo stesso grande filosofo e mistico Plotino non incoraggiò forse a guardare in se stessi anziché all’esterno, perché da dentro è possibile contemplare il Nous (Spirito-Intelletto), che è divino, nel quale è scritta la struttura profonda dell’Universo? Si pensi a quello che aveva detto lo stesso Shroedinger.
Dopo millenni e millenni di dibattiti, argomentazioni, teorie, modelli, meditazioni, contemplazioni, immedesimazioni sofferte, miti e religioni è questa l’unica e ultima risposta: che siamo dentro una trappola senza possibilità di uscita? Sarebbe veramente il massimo dell’ironia se l’unica proposizione linguistica che un mistico possa formulare, senza contraddire Lao Tse, fosse che l’Io costruisce un mondo “a propria immagine” più o meno “adeguato”, senza essere consapevole di farlo, poi “sente” questo mondo, “esterno” e indipendente da sè, infine costruisce l’Io stesso a fronte della realtà di quel mondo ritenuto oggettivo, perdendosi in un frattale se scopre il gioco!
Le conseguenze positive che ne derivano sul piano sociale (tolleranza, e pluralismo, responsabilità personale, distacco dalle proprie percezioni e valori a favore di altri…), certamente non bilanciano l’ambito circolare in cui rimane imprigionata la creatività umana.
Infine certe attuali tendenze psicologiche (16) sostengono una dualità interattiva nella conformazione della mente. L’evoluzione del cervello dapprima avrebbe favorito lo sviluppo del lato destro, preposto essenzialmente ad una comunicazione empatica con la Natura, tanto da permettere l’ascolto delle “Voci degli Dei”, mentre il lato sinistro, oggi sede della consapevolezza razionale e della individualità, rimaneva in ombra permettendo comportamenti forse più conformi al vivere in gruppo, con scarsa consapevolezza dell’Io. Successivamente si ha una rivoluzione cerebrale dalla quale emerge e domina l’emisfero sinistro in tutta la sua complessità e potenza, atto alle analisi consapevoli e alle certezze sull’esistenza dell’Io, ove prevale la visione razionale all’atto uditivo di ascoltare gli Dei. Non ne deriva forse che per comunicare col Dio (e quindi cogliere la Verità) è necessario un processo di annullamento dell’Io nel cosmo?
“Non si può negare ciò che non si conosce”, affermano spesso gli Scritti Sacri e “di ciò che non si può parlare si deve tacere” (settima e ultima proposizione del Tractatus), ma forse è un “tacere” che apre altre direttrici di esperienza, in un mondo come l’attuale nel quale si sta riscoprendo la narrazione epica e il mito.
(Piero Pistoia)
BIBLIOGRAFIA
1-Galilei “Dialogo sopra i due massimi sistemi del mondo” Salani, 1964
2-K. Popper “La logica della scoperta scientifica” Einaudi, 1970
3-O. Tobisco “ La crisi dei fondamenti” Borla, 1984
4-C. Hempel “Filosofia delle scienze naturali” Il Mulino, 1968, pag. 20-21
5-A.V. “Critica e crescita della Conoscenza” Feltrinelli,1976
6-P. Feyerabend “Addio alla Ragione” Armando,1990
7-M. Cerutti “La danza che crea” Feltrinelli,1989
8-I. Kant “Prolegomeni”, Laterza, 1982
9-I. Kant “Critica della Ragione Pura” Laterza, 1966
10-A. V. “La realtà inventata”, Feltrinelli, 1989, pag.17-35
11-B. Russell “L’analisi della materia” Longanesi,1964, pag. 293-29
12-E. Stein “Il problema dell’empatia” Studium,1984
13-L. Wittgenstein “Tractatus logico-philosophicus” Fratelli Bocca,1954
14-Lao Tse “Tao Te Ching” Adelphi,1980
15-L. S. Lerner et al. “Giordano Bruno” Le Scienze, N.58
16-Jaines “Il crollo della Mente Bicamerale” Adelphi, 1988
Per leggere il curricolo di piero pistoia cliccare sotto:
piero-pistoia-curriculumok (#)
Testo rivisitato da ‘Il Sillabario’ n. 3 1998
INTERMEZZO: breve poesia di Antonio machado
Il sillabario 2013 